Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BusyBoxesAutomaton

Source Notebook

Implementation of the Busy Boxes 3D reversible cellular automaton

Contributed by: Nikolay Murzin

ResourceFunction["BusyBoxesAutomaton"][init]

runs the BusyBoxes cellular automaton rule starting from an initial 3D state init.

ResourceFunction["BusyBoxesAutomaton"][init,n]

runs for n steps.

ResourceFunction["BusyBoxesAutomaton"][init,-n]

runs for n steps in reverse.

ResourceFunction["BusyBoxesAutomaton"][init,n,phase]

runs with an initial integer phase.

ResourceFunction["BusyBoxesAutomaton"][state,"Step", phase]

take a single step of the automaton.

ResourceFunction["BusyBoxesAutomaton"][state,"Swaps", phase]

return an explicit list of swap rules for a single step starting from a state with an optional phase.

ResourceFunction["BusyBoxesAutomaton"][state,"Visualization"]

return a 3D visualization for a state.

ResourceFunction["BusyBoxesAutomaton"][arguments][state]

represents an operator form.

Details

BusyBoxes (BBX) is an implementation of the 3D reversible cellular automata developed by Ed Fredkin and Daniel B. Miller in their 2005 paper, Two State, Reversible, Universal Cellular Automata In Three Dimensions. A preprint is available here.
This function was inspired by the online implementation at busyboxes.org.
The rules of this Cellular Automata are as follows: - Play takes place on a 3D Cartesian state of cells. - Each cell in the state is either odd or even, depending on whether the sum of the three coordinates specifying that cell's location in the state is odd or even. -Cells are either 1 or 0. 1 cells are shown as red if they are even, or blue if they are odd. 0 cells are not shown. -There are six phases in the evolution of the CA, numbered 0 to 5. During even phases, only even cells are operated on. During odd phases, odd cells are operated on. -During phase 0 and 3, the planar rule is applied to the XY plane. During phase 1 and 4, it is applied to the YZ plane. During phase 2 and 5, it is applied to the ZX plane. -The planar rule is this: for each diagonally situated pair of cells on the plane, if a 1 exists at either of the pair's knight's move positions, the value of the two cells in that diagonal pair is swapped. However, this only happens if there is no conflicting swap for either cell. -The knight's move positions for a diagonal pair of cells are the cells that can be reached from both cells in the pair by moving two in one axis and one in another. A picture helps:

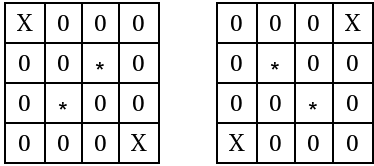
-The X's are the knight's move positions for the pairs of cells represented by asterisks.

Initial state can be either an array of 0s and 1s or a list of explicit positions of 1s. If an array is given swap outside its boundary are not allowed.
Note that since only swaps are allowed, the number of 1's and 0's is fixed for any set of initial conditions. One may think of the BBX CA as a set of rules for moving 1's around on the state.
Initial phase for forward direction is 0.
Running BBX backward with no specified initial phase will automatically choose a phase to undo the same number of steps in forward direction.
"Visualization" property takes the "Grid" option that can be either True or False.

Examples

Basic Examples (2) 

Run BusyBoxesAutomaton starting from a random initial condition for a single step:

In[1]:=
ResourceFunction["BusyBoxesAutomaton"][RandomInteger[1, {6, 6, 6}]]
Out[1]=

Run BusyBoxesAutomaton for 3 steps and visualize it:

In[2]:=
ResourceFunction["BusyBoxesAutomaton"]["Visualization"] /@ ResourceFunction["BusyBoxesAutomaton"][ RandomChoice[{.9, .1} -> {0, 1}, {6, 6, 6}], 3]
Out[2]=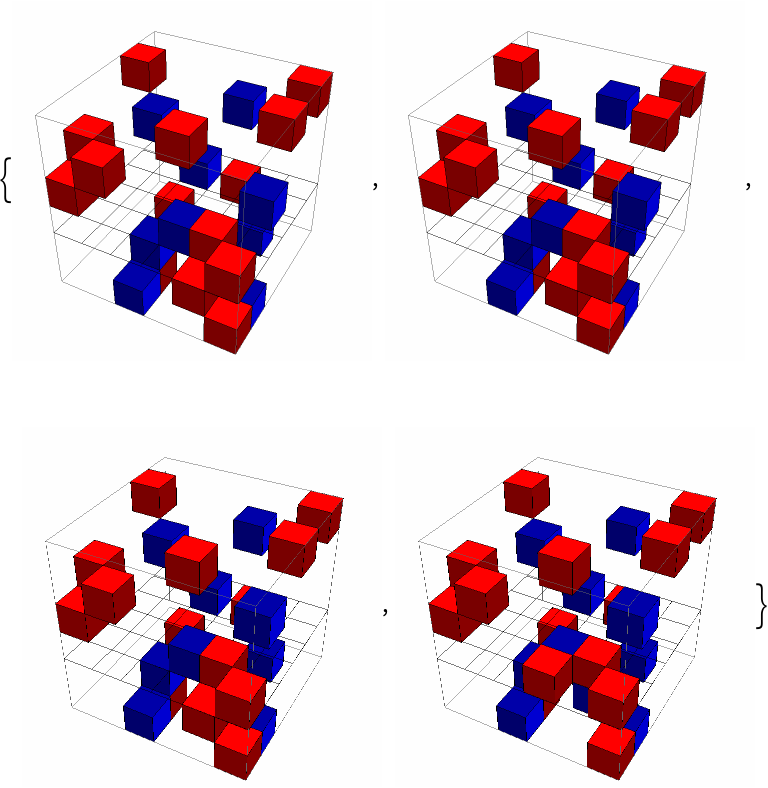

Run BBX for 100 steps and 100 more in reverse:

In[3]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e8d6e1eb-cc24-4be4-8344-62551d972b4c"]
Out[3]=

Neat Examples (2) 

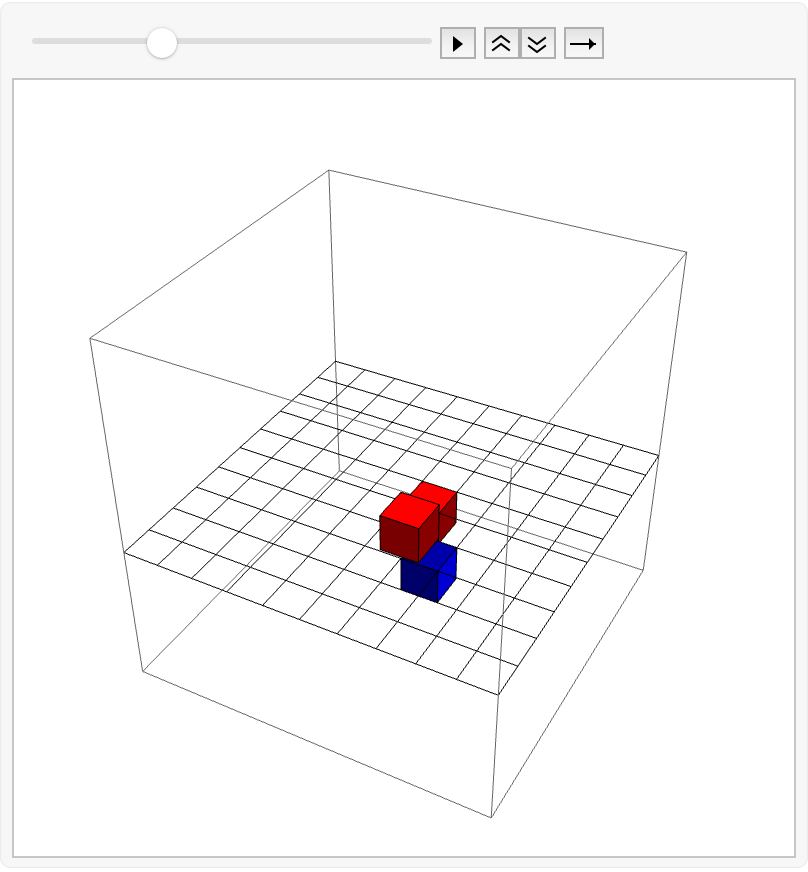Gliders:

In[4]:=
glider1 = SparseArray[{{11, 12, 12} -> 1, {13, 13, 12} -> 1}, {24, 24, 24}]; glider2 = SparseArray[{{12, 11, 14} -> 1, {13, 13, 14} -> 1, {14, 15, 14} -> 1, {15, 17, 14} -> 1}, {24, 24, 24}]; glider3 = SparseArray[{{14, 9, 16} -> 1, {14, 11, 16} -> 1, {13, 11, 16} -> 1, {13, 13, 16} -> 1, {19, 19, 16} -> 1}, {24, 24, 24}]; glider4 = SparseArray[{{15, 9, 18} -> 1, {14, 9, 18} -> 1, {14, 11, 18} -> 1, {13, 11, 18} -> 1, {13, 13, 18} -> 1}, {24, 24, 24}];
In[5]:=
ListAnimate[ ResourceFunction["BusyBoxesAutomaton"]["Visualization"] /@ ResourceFunction["BusyBoxesAutomaton"][glider3, 1000], SaveDefinitions -> True]
Out[5]=

Circular motion:

In[6]:=
makeBBCircularMotion[n : _Integer?Positive : 3] := Block[{start}, start = {2, -2, 2}; Prepend[ FoldList[Plus, start, Take[Catenate@Table[{{0, 1, -2}, {0, 2, -1}}, Ceiling[n/2]], n]], start + {-2, -1, 0}] ] makeBBCircularMotion[n : _Integer?Positive : 3, size_Integer] := SparseArray[Thread[makeBBCircularMotion[n] -> 1], ConstantArray[size, 3]]
In[7]:=
Dynamic[If[ListQ[traces], Show[ResourceFunction["BusyBoxesAutomaton"][traces[[-1]], ConstantArray[MinMax[traces] + {-1, 1}, 3], "Visualization", "Grid" -> False], If[ListQ[traces], Graphics3D[{Green, Point /@ Mean /@ traces}], Nothing]], "Run the next cell to start animation"]]
Out[7]=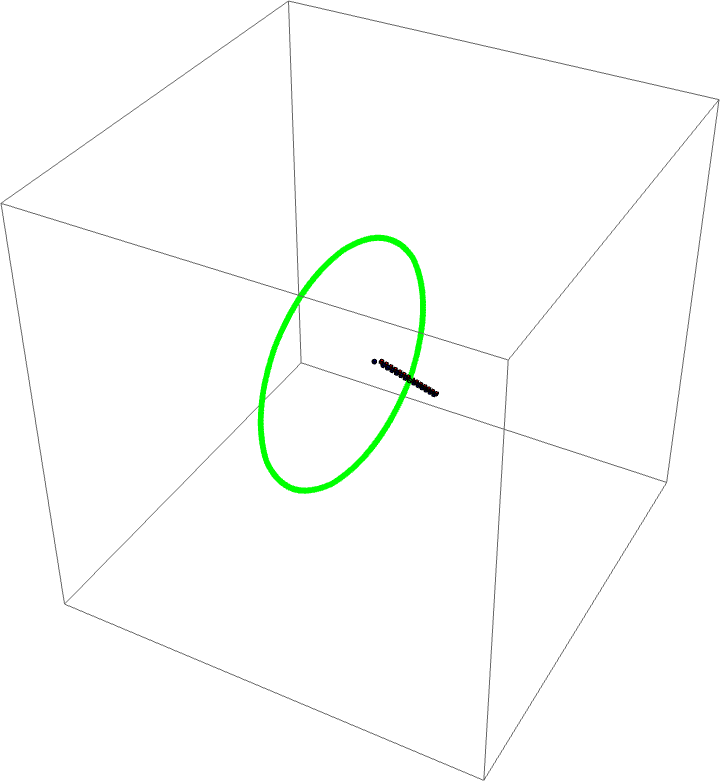

Start tracking circular motion:

In[8]:=
n = 28; traces = {makeBBCircularMotion[n - 2]}; phase = 0; Until[traces[[1]] === traces[[-1]], AppendTo[traces, ResourceFunction["BusyBoxesAutomaton"][traces[[-1]], "Step", phase]]; phase = Mod[phase + 1, 6]; ]

Show the circular motion:

In[9]:=
Show[ResourceFunction["BusyBoxesAutomaton"][Catenate[traces], "Visualization", "Grid" -> False], Graphics3D[{Green, Point /@ Mean /@ traces}], PlotRange -> Full]
Out[9]=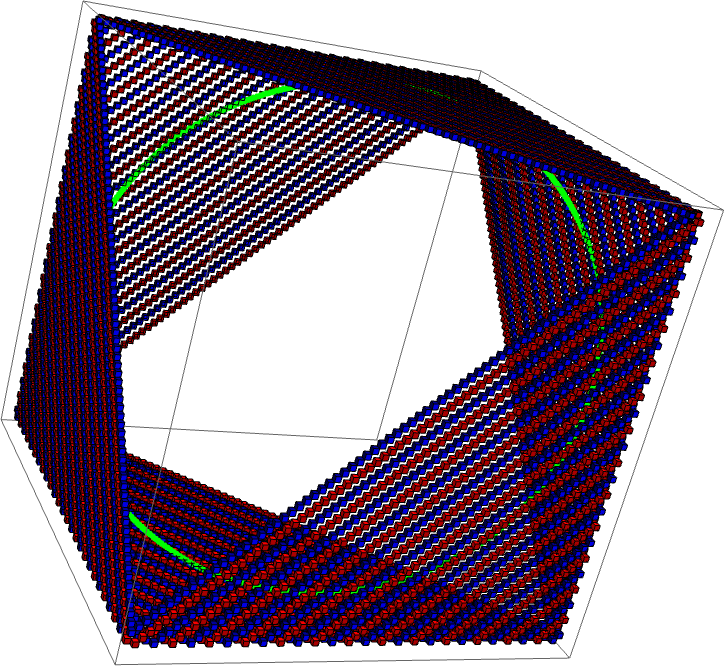

Compute box traces for all sizes up-to 100:

In[10]:=
allTraces = Monitor[Table[ NestWhileList[{ResourceFunction["BusyBoxesAutomaton"][#[[1]], "Step", #[[2]]], Mod[#[[2]] + 1, 6]} &, {makeBBCircularMotion[n - 2], 0}, Length[{##}] < n || #1[[1]] != {##}[[-1, 1]] &, All][[;; -2, 1]], {n, 3, 100, 1}], n]; // AbsoluteTiming
Out[10]=

Plot circularity dependency on the number of boxes measured as standard deviation of average radius for each step:

In[11]:=
ListPlot[ MapIndexed[{#2[[1]] + 2, StandardDeviation[#]/Mean[#] &[ Norm /@ (Mean /@ # - Threaded[Mean[Catenate[#]]])]} &, N@allTraces]]
Out[11]=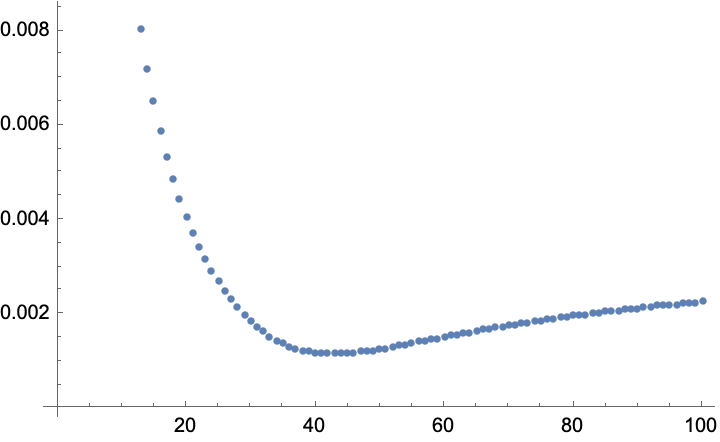

Which proves Miller and Fredkin hypothesis wrong of circularity monotonically decreasing to zero. They've only computed this curve up-to 20 boxes, but the minimum is at 43.

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 18 August 2023
  • 1.0.0 – 07 August 2023

Source Metadata

  • Citation:
    • Miller, Daniel B., and Edward Fredkin. "Two-state, reversible, universal cellular automata in three dimensions." Proceedings of the 2nd conference on Computing frontiers. 2005. DOI: 10.1145/1062261.1062271

Related Resources

License Information