Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BickleyKi

Source Notebook

Evaluate the Bickley function

Contributed by: Jan Mangaldan

ResourceFunction["BickleyKi"][n,z]

gives the Bickley function Kin(z).

Details and Options

Mathematical function, suitable for both symbolic and numerical manipulation.
The Bickley function satisfies , where K0(t) is the modified Bessel function BesselK.
ResourceFunction["BickleyKi"][n,z] has a branch cut discontinuity in the complex z plane running from -∞ to 0.
For certain special arguments, ResourceFunction["BickleyKi"] automatically evaluates to exact values.
ResourceFunction["BickleyKi"] can be evaluated to arbitrary numerical precision.
ResourceFunction["BickleyKi"] automatically threads over lists.

Examples

Basic Examples (3) 

Evaluate numerically:

In[1]:=
ResourceFunction["BickleyKi"][1, 5.1]
Out[1]=

Plot Ki1(z):

In[2]:=
Plot[ResourceFunction["BickleyKi"][1, x], {x, 0.5, 3}]
Out[2]=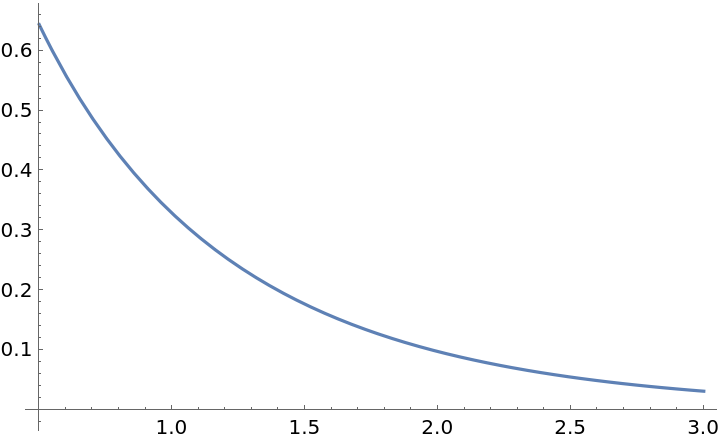

Series at the origin:

In[3]:=
Series[ResourceFunction["BickleyKi"][1, x], {x, 0, 3}]
Out[3]=

Scope (4) 

Evaluate for complex arguments and orders:

In[4]:=
ResourceFunction["BickleyKi"][2 + 3 I, 1.7 - 5. I]
Out[4]=

Evaluate to high precision:

In[5]:=
N[ResourceFunction["BickleyKi"][2, 3], 50]
Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=
ResourceFunction[ "BickleyKi"][2, 3.000000000000000000000000000000000000]
Out[6]=

BickleyKi threads elementwise over lists:

In[7]:=
ResourceFunction["BickleyKi"][{1, 2, 3}, 2.]
Out[7]=

Applications (4) 

Plot a complex-ordered Bickley function over the complex plane:

In[8]:=
Plot3D[Im[ResourceFunction["BickleyKi"][1 + I, x + I y]], {x, -2, 2}, {y, -2, 2}]
Out[8]=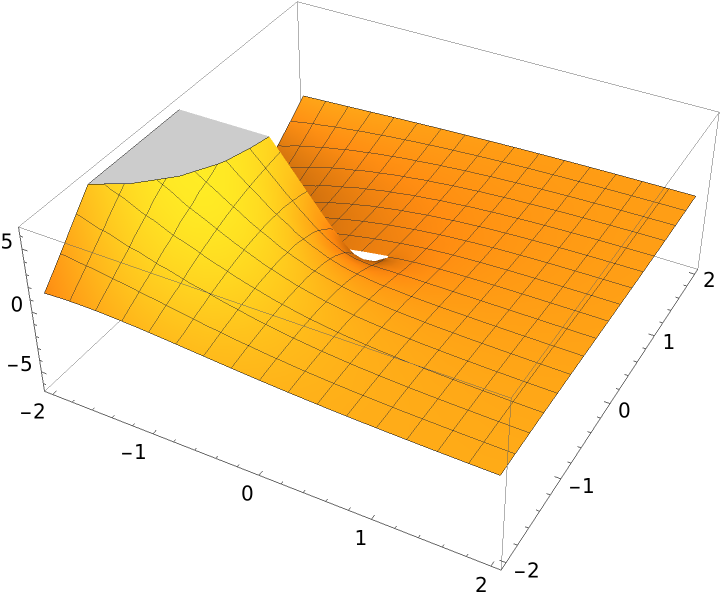

Average probability that a neutron travels across two parallel lines separated by a distance h without a collision:

In[9]:=
With[{h = 2/3}, N[ResourceFunction["BickleyKi"][2, h]]]
Out[9]=

Compare with the integral representation:

In[10]:=
With[{h = 2/3}, NIntegrate[Exp[-h Csc[t]] Sin[t], {t, 0, Pi}]/2]
Out[10]=

Express a modified Bessel function of the second kind as a finite sum of Bickley functions:

In[11]:=
With[{n = 5}, BesselK[n, z] == 1/2 Sum[(2^n Pochhammer[-n/2, k] Pochhammer[(1 - n)/2, k])/(k! Pochhammer[1 - n, k]) ResourceFunction["BickleyKi"][ 2 k - n, z], {k, 0, n - 1}]] // Simplify
Out[11]=

Properties and Relations (5) 

For n=0, BickleyKi is equal to K0(z):

In[12]:=
ResourceFunction["BickleyKi"][0, x] == BesselK[0, x]
Out[12]=

For n>0, BickleyKi is equal to an iterated integral of K0(z):

In[13]:=
With[{n = 5}, D[ResourceFunction["BickleyKi"][n, x], {x, n}] == (-1)^n BesselK[0, x]] // FullSimplify
Out[13]=

For n<0, BickleyKi is equal to (-1)nd-nK0(z)/dz-n:

In[14]:=
With[{n = 5}, ResourceFunction["BickleyKi"][-n, x] == (-1)^n Derivative[0, n][BesselK][0, x]] // FullSimplify
Out[14]=

Express a Bickley function of noninteger order in terms of simpler functions:

In[15]:=
ResourceFunction["BickleyKi"][-1/2, x] // FunctionExpand
Out[15]=

Compare BickleyKi with the integral definition:

In[16]:=
With[{n = 5, z = 11/3, prec = 20}, {N[ResourceFunction["BickleyKi"][n, z], prec], NIntegrate[BesselK[0, t] (t - z)^(n - 1), {t, z, Infinity}, WorkingPrecision -> prec]/Gamma[n]}]
Out[16]=

Possible Issues (2) 

Machine precision is not sufficient to obtain the correct result:

In[17]:=
ResourceFunction["BickleyKi"][10, N[20 + 30 I]]
Out[17]=

Use arbitrary-precision arithmetic instead:

In[18]:=
N[ResourceFunction["BickleyKi"][10, 20 + 30 I], 20]
Out[18]=

Version History

  • 2.0.0 – 11 March 2020
  • 1.0.0 – 03 December 2019

Source Metadata

  • Citation:
    • "Fractional Integrals." §10.43(iii) in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/10.43.iii. Release 1.0.24 of 2019-09-15.

Related Resources

License Information