Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the Bézout matrix of two univariate polynomials
ResourceFunction["BezoutMatrix"][poly1,poly2,var] returns the Bézout matrix of the polynomials poly1 and poly2 with respect to the variable var. |
The Bézout matrix of two polynomials:
| In[1]:= |
| Out[1]= |
The Bézout matrix of polynomials with numeric coefficients:
| In[2]:= |
| Out[2]= |
The Bézout matrix of polynomials with parametric coefficients:
| In[3]:= |
| Out[3]= | 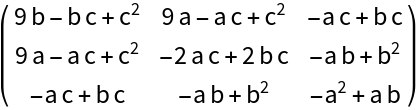 |
A polynomial is stable if all of its roots have negative real parts. Use BezoutMatrix to check the stability of a polynomial:
| In[4]:= | ![poly = 1 + x/2 + x^2/9 + x^3/72 + x^4/1008 + x^5/30240;
{qp, pp} = ComplexExpand[ReIm[poly /. x -> I x], TargetFunctions -> {Re, Im}];
MatrixForm[ma = ResourceFunction["BezoutMatrix"][pp, qp, x]]](https://www.wolframcloud.com/obj/resourcesystem/images/1b0/1b048c21-019c-4ea0-bcc7-6644f612e367/2ca4662d77290bb5.png) |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |
Verify stability by computing the roots of the polynomial:
| In[8]:= |
| Out[8]= |
The Bézout matrix is symmetric:
| In[9]:= |
| Out[9]= |
The determinant of the Bézout matrix of two polynomials is proportional to their resultant:
| In[10]:= | ![pp = 11 (x - 1) (x - 2) (x - 3) (x - 4);
qp = -9 (x - 5) (x - 6) (x - 7);
m = Exponent[pp, x]; n = Exponent[qp, x];](https://www.wolframcloud.com/obj/resourcesystem/images/1b0/1b048c21-019c-4ea0-bcc7-6644f612e367/097706b21846d4ca.png) |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
Verify a relationship between the Bézout matrix and the Sylvester matrix:
| In[13]:= |
| In[14]:= |
| In[15]:= |
| In[16]:= |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License