Function Repository Resource:

BKKRootBound

Source Notebook

Compute the BKK bound on the number of isolated complex solutions of a square polynomial system

Contributed by: Adam Strzeboński

ResourceFunction["BKKRootBound"][polys, vars]

computes the BKK bound on the number of isolated common roots of polynomials polys in variables vars.

ResourceFunction["BKKRootBound"][polys, vars, "Toric"]

computes the BKK bound on the number of isolated common roots with all non-zero coordinates.

Details

The BKK bound is a bound on the number of common roots based on the Bernstein–Khovanskii–Kushnirenko (BKK) theorem.

When the set of monomials present in each of polys is fixed, the number of common roots is equal to the bound for a generic choice of coefficients.

ResourceFunction["BKKRootBound"] counts roots by multiplicity.

Examples

Basic Examples (2)

Compute the BKK bound for a system of polynomials:

In[1]:=

$ResourceFunction["BKKRootBound"][{x^2 + 2 y + 3, 4 x y + 5}, {x, y}]$

Out[1]=

For this system the number of roots is equal to the bound:

In[2]:=

$SolveValues[{x^2 + 2 y + 3 == 0, 4 x y + 5 == 0}, {x, y}]$

Out[2]=

Scope (3)

Define a family of polynomial systems indexed by an integer n:

In[3]:=

$cyclic[n_] := Append[Table[ Sum[Product[x[Mod[i, n, 1]], {i, j, j + k}], {j, n}], {k, 0, n - 2}], Product[x[i], {i, n}] - 1]$

Compute the BKK bound for n=5:

In[4]:=

Out[4]=

Compute the actual number of roots:

In[5]:=

Out[5]=

BKK bound on the number of roots:

In[6]:=

$ResourceFunction["BKKRootBound"][{x^2 - x, x + y + 1}, {x, y}]$

Out[6]=

BKK bound on the number of roots with nonzero coordinates:

In[7]:=

$ResourceFunction[ "BKKRootBound"][{x^2 - x, x + y + 1}, {x, y}, "Toric"]$

Out[7]=

Compute the roots:

In[8]:=

$SolveValues[{x^2 - x == 0, x + y + 1 == 0}, {x, y}]$

Out[8]=

The number of roots may be strictly less than the BKK bound:

In[9]:=

$ResourceFunction["BKKRootBound"][{x^2 + x y + 1, x y + 1}, {x, y}]$

Out[9]=

In[10]:=

$SolveValues[{x^2 + x y + 1 == 0, x y + 1 == 0}, {x, y}]$

Out[10]=

The BKK bound depends only on monomials and not on coefficients:

In[11]:=

$gcf[] := RandomInteger[{-100, 100}] gpolys = {gcf[] x^2 + gcf[] x y + gcf[], gcf[] x y + gcf[]}$

Out[12]=

In[13]:=

Out[13]=

For generic coefficients the number of roots is equal to the BKK bound:

In[14]:=

Out[14]=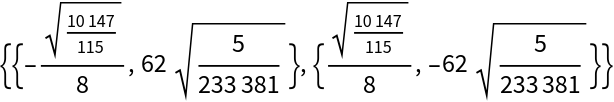

Possible Issues (1)

BKKRootBound gives a bound on the number of isolated solutions. It gives finite values for systems that have infinitely many (necessarily non-isolated) solutions:

In[15]:=

$ResourceFunction["BKKRootBound"][{x^2 - y^2, x - y}, {x, y}]$

Out[15]=

In[16]:=

$Solve[{x^2 - y^2 == 0, x - y == 0}, {x, y}]$

Out[16]=

Publisher

Adam Strzebonski

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

1.0.0 – 31 May 2024

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License