Basic Examples (2)
Find the arithmetic derivative of 100:
Find the arithmetic derivative of the fraction 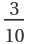 :
:
Scope (2)
Arithmetic derivate for any prime is 1:
Using Leibniz rule it is easy to find the formula for prime tower :
which is the same as :
Properties and Relations (4)
Higher order arithmetic derivatives are defined successively by nesting the same operation multiple times:
Arithmetic derivative of an integer n has the following bounds: 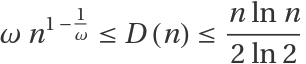 , where is PrimeOmega[n] and gives the number of prime factors counting multiplicities.
, where is PrimeOmega[n] and gives the number of prime factors counting multiplicities.
The equality of the lower bound holds if and only if :
The equality of the upper bound holds if and only if n is prime or a prime tower:
if and only if where p is any prime:
It is easy to see that is not a fixed point:
has nontrivial solution for some rational value x:
Possible Issues (2)
The arithmetic derivative does not obey linearity in general:
Clearly 1 is not same as :
However, if we find some m and n such that , then for all integer k. For instance:
Then the following also true:
Neat Examples (4)
The graph of for
We can define the arithmetic integral by solving the equation given a, . The algorithm can be implemented with simple search in the interval found in the aforementioned bounds:
For example, the integrals of 10 and 100:
We also can find the a's that do not have their integrals less than 1000:
Here is a list of number with more than one integral:
The result means that 10 has two integrals, 12 has two integrals and so on.
The Goldbach conjecture implies that the differential equation has a positive integer solution for any natural number :
For instance as a sum of two primes:
By the Leibniz rule of arithmetic derivative, 35 is one solution for n such that the differential equation holds:
Twin prime conjecture implies that the differential equation has infinite number of solutions:
This is from the application of Leibniz rule on the arithmetic derivative of where p is any prime:
In general, . If is a prime again,
Thus we shall have infinite such if the conjecture holds.
![]() :
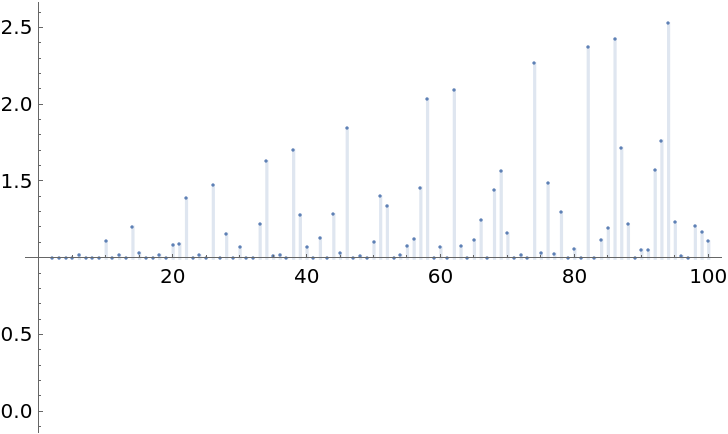
:![]() , where is PrimeOmega[n] and gives the number of prime factors counting multiplicities.
, where is PrimeOmega[n] and gives the number of prime factors counting multiplicities.![DiscretePlot[
ResourceFunction["ArithmeticD"][n]/
With[{omega = PrimeOmega[n]}, omega*n^(1 - 1/omega)]
, {n, 1, 100},
PlotRange -> All, AxesOrigin -> {0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/06d/06d3a6ea-9a8b-476e-8e1e-704abdf3db54/1-0-0/3bfac7a08ee040e7.png)
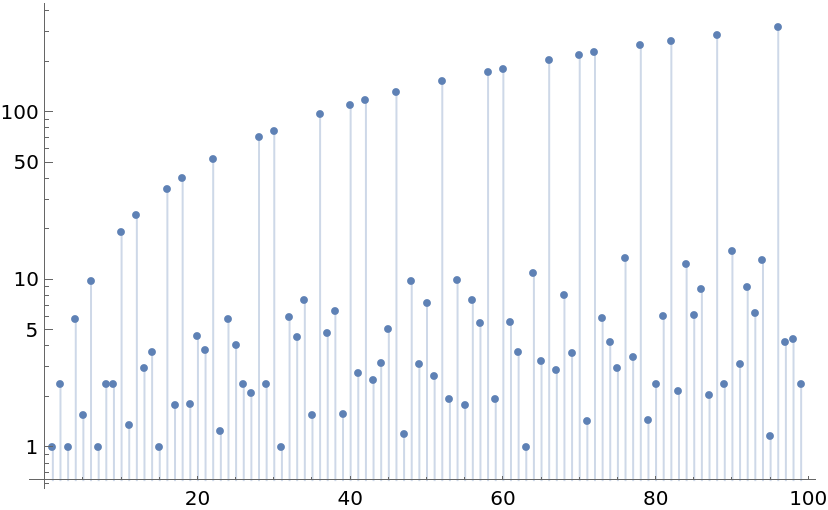
![ListLogPlot[
Table[((n*Log[n])/(2*Log[2]))/ResourceFunction["ArithmeticD"][n]
, {n, 2, 100}], Sequence[
PlotRange -> All, AxesOrigin -> {0, 0}, Filling -> Bottom, PlotStyle -> PointSize[0.01]]]](https://www.wolframcloud.com/obj/resourcesystem/images/06d/06d3a6ea-9a8b-476e-8e1e-704abdf3db54/1-0-0/166ff12dd5cb07a8.png)

![LaunchKernels[];
res = ParallelMap[{#, ArithmeticILength[#]} &, Range[2, 1000]];
Cases[res, _?(#[[2]] == 0 &)][[All, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/06d/06d3a6ea-9a8b-476e-8e1e-704abdf3db54/1-0-0/153aa278cc7d67d2.png)


