Compute the integral describing the area between two plane curves
Contributed by:
Wolfram|Alpha Math Team
Examples
Basic Examples (3)
Compute an integral representing the area between two curves:
Plot the region:
Activate the integral to compute the area:
Scope (4)
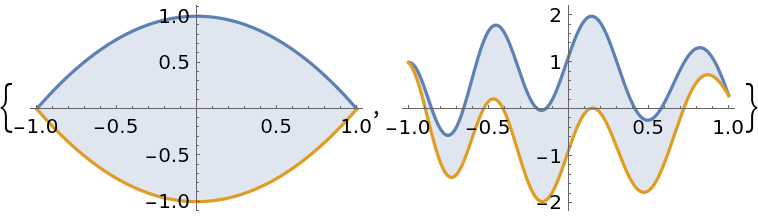
Find the area of the region enclosed by two curves:
Plot the region in question:
A region where the curves do not meet:
With multiple enclosed regions, the integrand will use Abs to return a positive area:
Visualize the regions:
Find the area between two curves containing parameters:
Options (2)
Assumptions
The result may be conditioned on parameters:
Make an assumption about the parameter to then evaluate the area:
Applications (2)
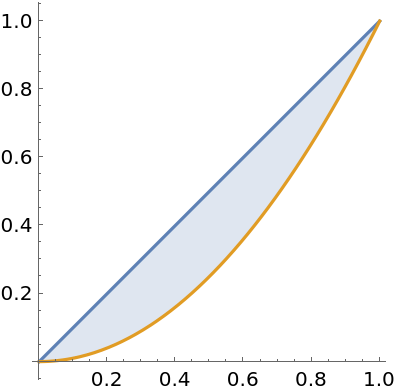
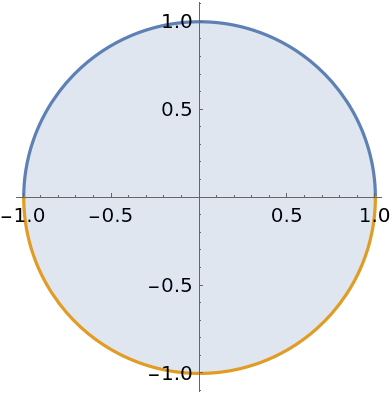
Compute the area of a disk:
Visualize the disk:
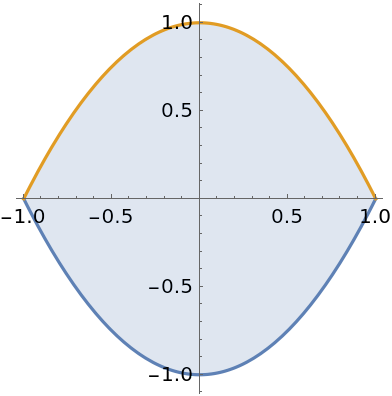
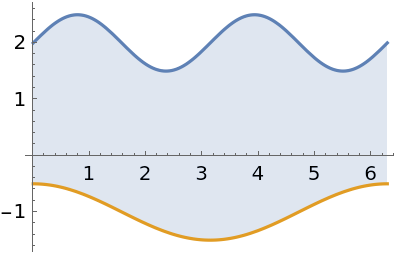
Cavalieri's principle states that the area between two curves does not change when each curve is shifted by the same amount. Here are three functions:
Compute an integral representing the area between f and g:
This is the same as the integral obtained after shifting both f and g by h:
Though their areas are the same, the regions are very different:
Properties and Relations (3)
Find the integral representing the area between sin(x) and cos(x) over the interval (0,π):
Activate the integral to compute the area:
Use the resource function AreaBetweenCurves to compute the area directly:
Publisher
Wolfram|Alpha Math Team
Related Links
Version History
-
2.0.0
– 23 March 2023
-
1.0.0
– 11 May 2020
Related Resources
Author Notes
To view underlying source code, evaluate the following:
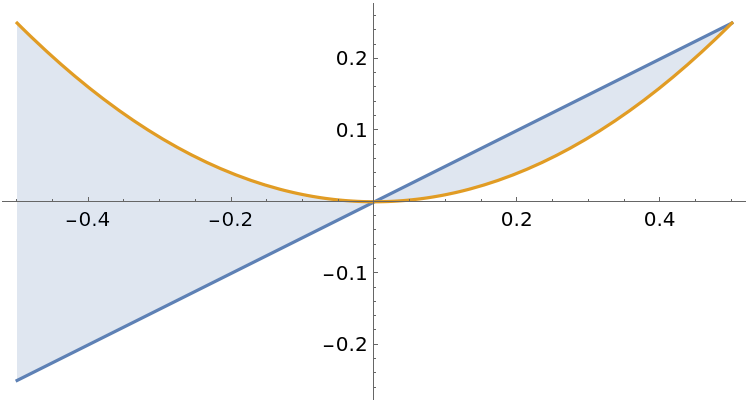
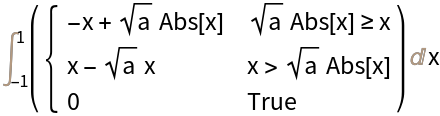
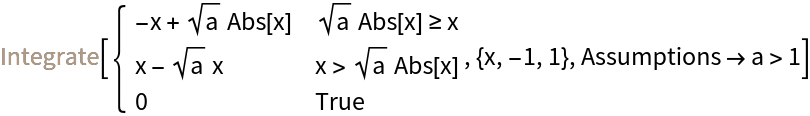
![f = 1 - x^2;
g = x^2 - 1;
h = Sin[(x - 5)^2];](https://www.wolframcloud.com/obj/resourcesystem/images/776/77679577-caa8-4399-a283-144bdaff166e/1-0-0/2d5ccc09c082bdf2.png)