Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AngleBetweenPlanes

Source Notebook

Compute the angle between two planes in R^3

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["AngleBetweenPlanes"][plane1,plane2,vars]

computes the angle between the two planes plane1 and plane2 with respect to vars.

Details

The planes must be linear in at most three variables.

Examples

Basic Examples (1) 

Find the angle between two planes:

In[1]:=
ResourceFunction["AngleBetweenPlanes"][x + y + z == 3, x + y - z == 4, {x, y, z}]
Out[1]=

Scope (2) 

Find the angle between two planes:

In[2]:=
ResourceFunction["AngleBetweenPlanes"][x + y == 3, x + y - z == 4, {x, y, z}]
Out[2]=

Find the angle between two planes:

In[3]:=
ResourceFunction["AngleBetweenPlanes"][z == x, z == 0, {x, y, z}]
Out[3]=

Plot the two planes:

In[4]:=
Plot3D[{x, 0}, {x, -2, 2}, {y, -2, 2}]
Out[4]=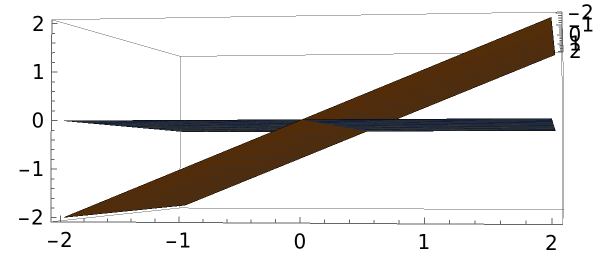

Obtain a half plane representation of the angle:

In[5]:=
Graphics3D[{HalfPlane[{{0, 0, 0}, {0, 1, 0}}, {1, 0, 1}], HalfPlane[{{0, 0, 0}, {0, 1, 0}}, {1, 0, 0}]}]
Out[5]=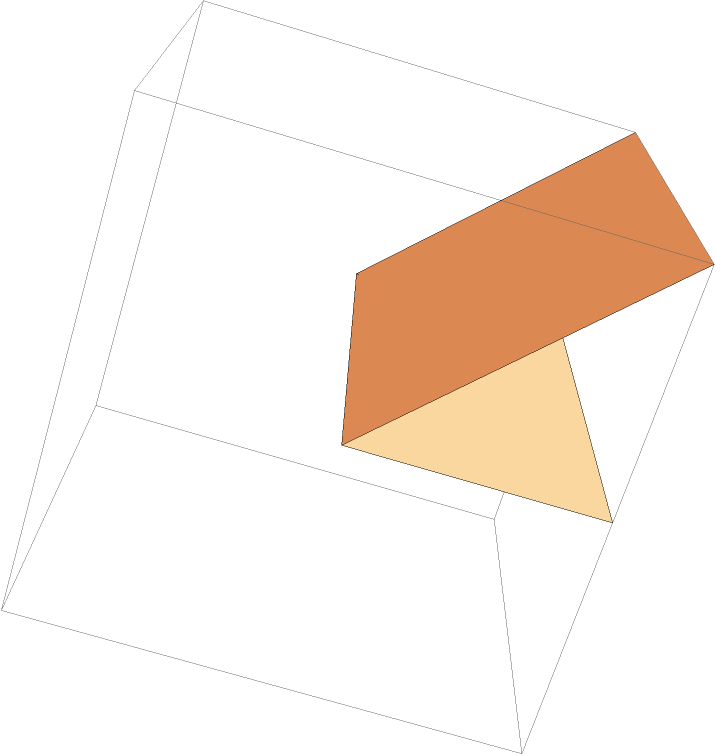

Verify the angles are equal:

In[6]:=
DihedralAngle[{{0, 0, 0}, {0, 1, 0}}, {{1, 0, 1}, {1, 0, 0}}] === ResourceFunction["AngleBetweenPlanes"][z == x, z == 0, {x, y, z}]
Out[6]=

Possible Issues (1) 

The functions must be linear:

In[7]:=
ResourceFunction["AngleBetweenPlanes"][x + y + z^2 == 3, x + y - z == 4, {x, y, z}]
Out[7]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 07 July 2021

Related Resources

Author Notes

To view the full source code for AngleBetweenPlanes, evaluate the following:

In[1]:=
SystemOpen[ FileNameJoin[{DirectoryName[FindFile["ResourceFunctionHelpers`"]], "AngleBetweenPlanes.wl"}]]

License Information