Basic Examples (5)
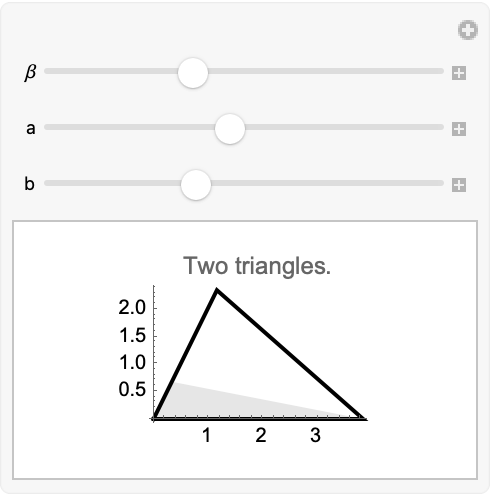
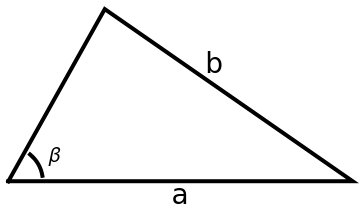
There are two triangles with the specified angle, side, side for this example:
The triangles above are the black outline and the gray triangle below:
The next two cells verify that both triangles above have the specified angle, side, side:
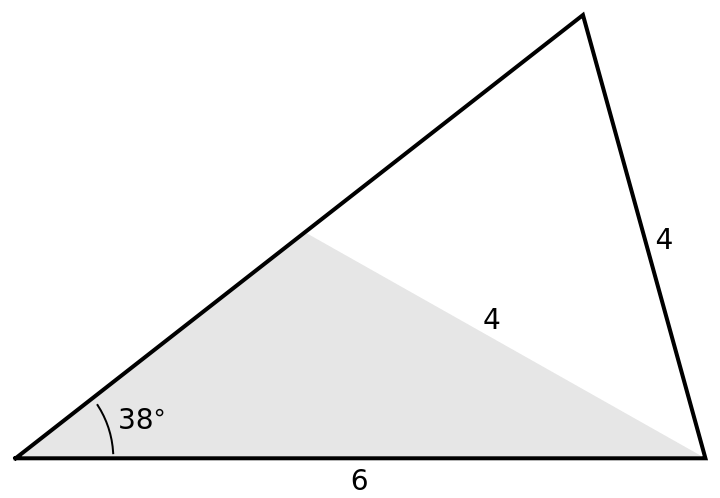
Only one triangle has the specified angle side, side in this example:
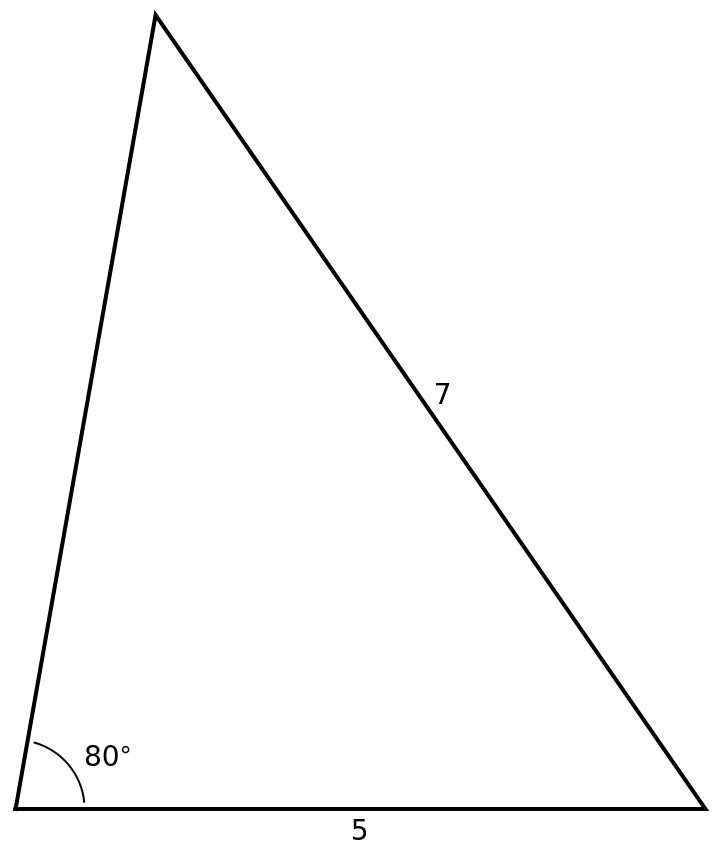
The next cell verifies the triangle above has the specified angle, side, side:
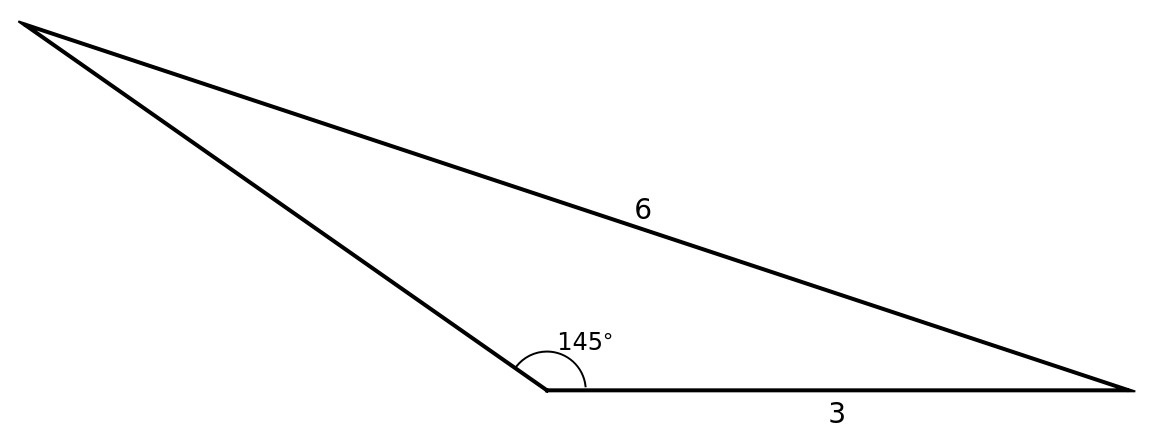
ASSTriangles always returns one obtuse triangle when the specified angle is 90° or greater and the third argument is greater than the second argument. An example is in the next cell:
The next cell verifies the triangle above has the specified angle, side, side:
The next example makes a (3,4,5) right triangle:
The next cell verifies the triangle above has the specified angle, side, side:
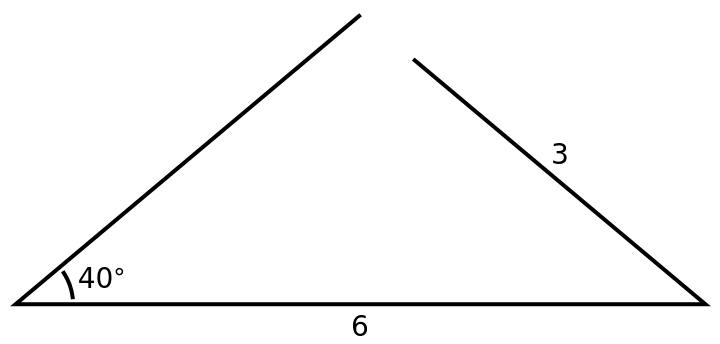
The next example is a case where no triangle has the specified angle, side, side:
In this example we would have a right triangle if the last argument of ASSTriangles was 6 Sin[40°]≈3.85673.
The next graphics illustrates why no triangle has the angle, side, side specified in the last example:
Scope (4)
When ASSTriangles is given exact input it returns exact results:
When ASSTriangles is given values with many digits of precision it returns results with all digits that can be be justified:
When one or more argument is symbolic and non-numeric ASSTriangles does nothing to change the input:
We can use replacement rules to assign specific values for a, b in triangles above:
We can also use Blockto assign values to a, b in triangles above:
ASSTriangles displays an error message and returns the original input when given incorrect:
No message is displayed in the next example because it would give a list of Triangles if b had an appropriate value:
![Graphics[{GrayLevel[0.9], triangle2, Black, Circle[{0, 0}, {0.85, 0.85}, {3 °, 33.0 °}], Text[Style["38°", 14], {1.1, 0.33}],
Text[Style["6", 14], {3, -0.2}], Text[Style["4", 14], {5.65, 1.9}], Text[Style["4", 14], {4.15, 1.2}], AbsoluteThickness@2, Line[Join[Part[triangle1, 1], {Part[triangle1, 1, 1]}]]}, AspectRatio -> Automatic, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/612878cb21725bbb.png)
![{p1, p2, p3} = Part[triangle1, 1];
{Apply[ArcTan, p3]*180/\[Pi], Norm[p1 - p2], Norm[p2 - p3]}](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/55a39a7ef94c8b92.png)
![{p1, p2, p3} = Part[triangle2, 1];
{Apply[ArcTan, p3]*180/\[Pi], Norm[p1 - p2], Norm[p2 - p3]}](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/1479d8ae329f0d1d.png)
![Graphics[{White, EdgeForm@{AbsoluteThickness@2, Black}, First@triangle, Black, Black,
Circle[{0, 0}, {0.5, 0.5}, {6 °, 74 °}], Text[Style["80°", 14], {0.67, 0.38}],
Text[Style["5", 14], {2.5, -0.16}], Text[Style["7", 14], {3.1, 3}]},
AspectRatio -> Automatic, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/132d7a19130789d7.png)
![{p1, p2, p3} = Part[triangle, 1, 1];
{Apply[ArcTan, p3]*180/\[Pi], Norm[p1 - p2], Norm[p2 - p3]}](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/64bd08c00ae8449b.png)
![Graphics[{White, EdgeForm@{AbsoluteThickness@2, Black}, First@obtuseTriangle, Black,
Circle[{0, 0}, {0.2, 0.2}, {6 °, 142 °}],
Text[Style["145°", 12], {0.2, 0.25}],
Text[Style["3", 14], {1.5, -0.12}], Text[Style["6", 14], {0.5, 0.93}]}, AspectRatio -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/1c579e36066f2818.png)
![{p1, p2, p3} = Part[obtuseTriangle, 1, 1];
{Apply[ArcTan, p3]*180/\[Pi], Norm[p1 - p2], Norm[p2 - p3]}](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/0da834b96fd8df9b.png)
![Graphics[{White, EdgeForm@{AbsoluteThickness@2, Black}, rightTraingle,
Black, Text[Style["3", 14], {0.78, 1.2}], Text[Style["4", 14], {3.3, 1.4}]}, Axes -> True, AspectRatio -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/46979f51e21215e8.png)

![{p1, p2, p3} = Part[rightTraingle, 1];
{ArcCos[p3 . (p2 - p3)] 180/\[Pi], Norm[p1 - p2], Norm[p2 - p3]}](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/715e03543fe6e682.png)
![Graphics[{AbsoluteThickness@2, Line[{3.9 { Cos[40 °], Sin[40 °]}, {0, 0}, {6, 0}, {6 + 3.3 Cos[140 °], 3.3 Sin[140 °]}}],
Circle[{0, 0}, {0.5, 0.5}, {7 °, 33 °}], Text[Style["40°", 14], {0.75, 0.22}],
Text[Style["6", 14], {3, -0.2}], Text[Style["3", 14], {4.74, 1.3}]},
AspectRatio -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/452c10465c39c231.png)
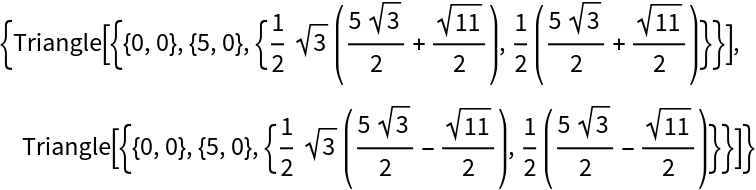
![Manipulate[
DynamicModule[{triangles, failed = False}, Quiet[triangles = Check[ResourceFunction["ASSTriangles"][\[Beta] °, a, b], failed = True]];
Which[failed, Pane[Style["ASSTriangles was given invalid arguments", 18, Bold], Sequence[
ImageSize -> {200, 100}, Alignment -> {Center, Center}]],
failed = False; Length[triangles] == 1,
Graphics[{White,
EdgeForm[{
AbsoluteThickness[2], Black}],
First[triangles]}, PlotLabel -> "One triangle", AspectRatio -> Automatic, Axes -> True, ImageSize -> {200, 100}],
Length[triangles] == 2,
Graphics[{GrayLevel[0.9], Last@triangles, AbsoluteThickness@2, Opacity[1, Black], Line[Join[Part[triangles, 1, 1], {Part[triangles, 1, 1, 1]}]]}, AspectRatio -> Automatic, Axes -> True, ImageSize -> {200, 100}, PlotRange -> All, PlotLabel -> "Two triangles."],
True, Pane[Style["No solution.", 18], ImageSize -> {200, 100}, Alignment -> {Center, Center}]
]],
{{\[Beta], 60}, 2, 175}, {{a, 4}, 0.3, 8}, {{b, 6}, 1, 8}
]](https://www.wolframcloud.com/obj/resourcesystem/images/770/770726f5-fce4-47fc-bf3f-d90a39bfbf89/1-0-0/532ec9a74ec10af8.png)