Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Szeged index of an undirected graph or a molecule
ResourceFunction["SzegedIndex"][g] computes the Szeged index of the graph g. | |
ResourceFunction["SzegedIndex"][mol] computes the Szeged index of the molecule mol. |
The Szeged index of a Petersen graph:
| In[1]:= |
| Out[1]= |
Compute the Szeged index of a molecule:
| In[2]:= | ![ResourceFunction["SzegedIndex"][
Molecule[{"C", "C", "C", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 7}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{7, 3}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{1, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{2, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{7, 18}, "Single"],
Bond[{7, 19}, "Single"]}, {}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9df/9df42d27-0431-430a-a679-305a23a85ca9/5552c16bb071743d.png) |
| Out[2]= |
Compute the Szeged index of a named entity:
| In[3]:= |
| Out[3]= |
By default, hydrogens are ignored in the computation of the Szeged index:
| In[4]:= |
| Out[4]= |
Use IncludeHydrogens→All to account for hydrogens:
| In[5]:= |
| Out[5]= |
Generate all alkanes with 7 carbon atoms (heptanes) using the resource function AlkaneIsomers:
| In[6]:= |
| Out[6]= | 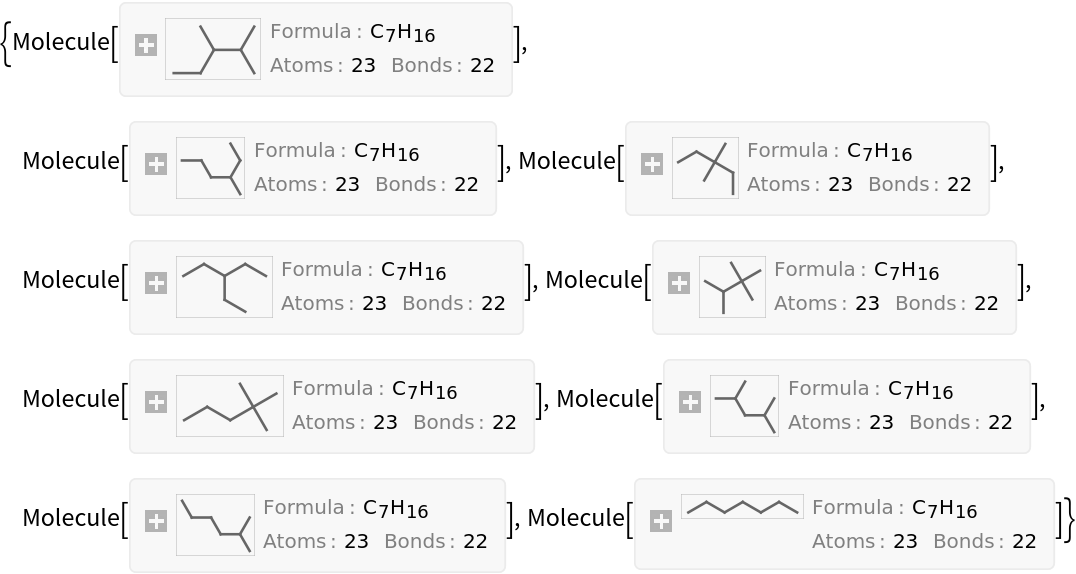 |
Sort the heptane isomers by their Szeged index. This effectively sorts them from "most branched" to "least branched":
| In[7]:= |
| Out[7]= | 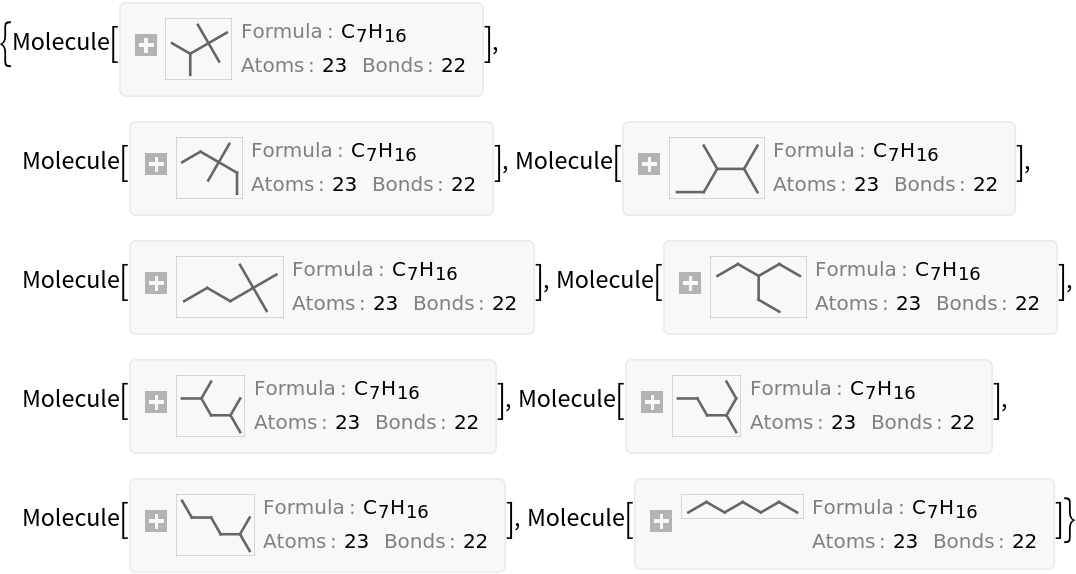 |
Define a function for computing the Wiener index of a graph:
| In[8]:= |
For an acyclic graph, the Szeged index is equivalent to the Wiener index:
| In[9]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null, {{3, 4}, {5, 6}, {5, 3}, {7, 8}, {7, 1}, {7, 2}, {7, 3}, {9, 10}, {9, 2}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{0., 1.466033332275663}, {
0.7330166661378313, 1.466033332275663}, {
1.8325416653445783`, 1.466033332275663}, {
1.4660333322756627`, 0.7330166661378315}, {
2.199049998413494, 0.7330166661378315}, {2.199049998413494, 0.}, {1.2827791657412049`, 2.199049998413494}, {
2.5655583314824097`, 1.466033332275663}, {
0.7330166661378313, 0.7330166661378315}, {
0.7330166661378313, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 7}, {2, 7}, {2, 9}, {3, 4}, {3, 5}, {3, 7}, {5, 6}, {7, 8}, {9, 10}}, 0.027040802458717428`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.027040802458717428], DiskBox[2, 0.027040802458717428], DiskBox[3, 0.027040802458717428], DiskBox[4, 0.027040802458717428], DiskBox[5, 0.027040802458717428], DiskBox[6, 0.027040802458717428], DiskBox[7, 0.027040802458717428], DiskBox[8, 0.027040802458717428], DiskBox[9, 0.027040802458717428], DiskBox[10, 0.027040802458717428]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\);
{WienerIndex[g], ResourceFunction["SzegedIndex"][g]}](https://www.wolframcloud.com/obj/resourcesystem/images/9df/9df42d27-0431-430a-a679-305a23a85ca9/5935cda1df33d205.png) |
| Out[10]= |
The Szeged index is equal to half the sum of all elements of the Szeged matrix:
| In[11]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null, {{3, 4}, {5, 6}, {5, 3}, {7, 8}, {7, 1}, {7, 2}, {7, 3}, {9, 10}, {9, 2}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{0., 1.466033332275663}, {
0.7330166661378313, 1.466033332275663}, {
1.8325416653445783`, 1.466033332275663}, {
1.4660333322756627`, 0.7330166661378315}, {
2.199049998413494, 0.7330166661378315}, {2.199049998413494, 0.}, {1.2827791657412049`, 2.199049998413494}, {
2.5655583314824097`, 1.466033332275663}, {
0.7330166661378313, 0.7330166661378315}, {
0.7330166661378313, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 7}, {2, 7}, {2, 9}, {3, 4}, {3, 5}, {3, 7}, {5, 6}, {7, 8}, {9, 10}}, 0.027040802458717428`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.027040802458717428], DiskBox[2, 0.027040802458717428], DiskBox[3, 0.027040802458717428], DiskBox[4, 0.027040802458717428], DiskBox[5, 0.027040802458717428], DiskBox[6, 0.027040802458717428], DiskBox[7, 0.027040802458717428], DiskBox[8, 0.027040802458717428], DiskBox[9, 0.027040802458717428], DiskBox[10, 0.027040802458717428]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\);
ResourceFunction["SzegedIndex"][g] == Total[ResourceFunction["SzegedMatrix"][g], 2]/2](https://www.wolframcloud.com/obj/resourcesystem/images/9df/9df42d27-0431-430a-a679-305a23a85ca9/0a879d7e77cb4f89.png) |
| Out[12]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License