Basic Examples (4)
Use FullSimplifyFunction to simplify a simple Function:
Use FullSimplifyFunction to simplify a simple function given as a rule:
Use FullSimplifyFunction to simplify a more complicated function, even when some variables have global values assigned:
Use FullSimplifyFunction to simplify multiple function rules:
Scope (2)
Use FullSimplifyFunction to simplify expressions involving special functions:
Use FullSimplifyFunction with more complicated function rules:
Options (3)
Use FullSimplifyFunction with Assumptions:
Use FullSimplifyFunction to simplify a function involving an EllipticF using assumptions:
Use FullSimplifyFunction to simplify a function of two variables under specific assumptions:
Applications (3)
Use FullSimplifyFunction with the results of DSolve:
Use FullSimplifyFunction on the solutions:
Verify the solutions:
Solve an initial value problem for an inhomogeneous linear hyperbolic system with constant coefficients:
Use FullSimplifyFunction on the solutions:
Verify the solutions:
Use FullSimplifyFunction in the solutions of the Euler-Lagrange equations governing the motion of a rolling wheel on an inclined plane. In this particular problem, the translational coordinate y and the rotational coordinate θ are treated as independent variables. Define the equation of motion for the translational coordinate and its initial conditions:
The solution for equation of motion using DSolve:
Apply FullSimplifyFunction:
Verify the solution:
Use the resource function SymbolToSubscript to format some parts of the solution as subscripts:
The equation of motion for the rotational coordinate and its initial conditions:
The solution for this equation of motion using DSolve:
Verify the solution:
Use SymbolToSubscript to format some parts of the solution as subscripts:
Properties and Relations (2)
Use FullSimplifyFunction with the resource function SolutionRulesToFunctions:
Apply FullSimplifyFunction on the solution:
An equivalent way to obtain the same results is by using ExpressionToFunction, which ensures proper handling of variable substitution during simplification:
Possible Issues (1)
By design, FullSimplifyFunction applies FullSimplify to the function body while only wrapping the declared function variables with HoldPattern. Any other parameters in the expression are not automatically protected from evaluation. This behavior can be seen in the following example:
![ResourceFunction["FullSimplifyFunction"][
x -> Function[t, 1/6 E^(-Sqrt[3] t) (3 - 2 Sqrt[3] + 3 E^(2 Sqrt[3] t) + 2 Sqrt[3] E^(2 Sqrt[3] t)) C[1] - (
E^(-Sqrt[3] t) (-1 + E^(2 Sqrt[3] t)) C[2])/(2 Sqrt[3])]]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/36d9913027918f6e.png)
![ResourceFunction["FullSimplifyFunction"][
a -> Function[
x, -Log[(1 - E^(x k[1] + (k[1] (2 I \[Pi] C[1]))/k[1]))/k[1]]], Assumptions -> C[1] \[Element] Integers]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/4b685005323461ac.png)
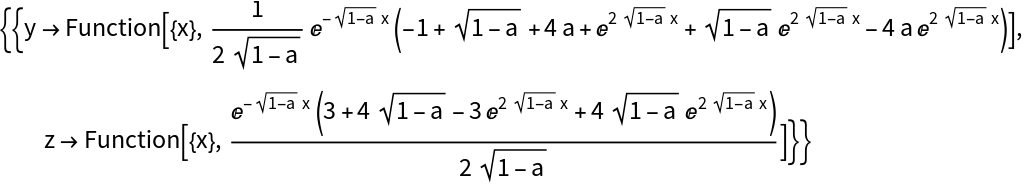
![pdes = {D[u[x, t], t] == D[v[x, t], x] + 1, D[v[x, t], t] == -D[u[x, t], x] - 1};
ic = {u[x, 0] == Cos[x]^2, v[x, 0] == Sin[x]};
sol = DSolve[{pdes, ic}, {u, v}, {x, t}]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/4b5f2319681ddb3d.png)
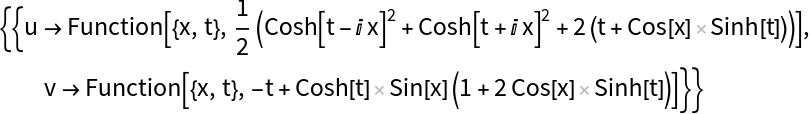
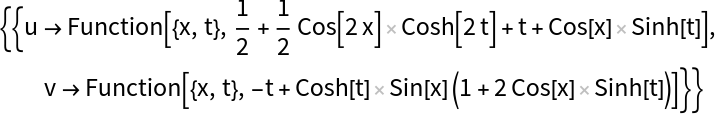
![ResourceFunction["SymbolToSubscript"][
ResourceFunction["FullSimplifyFunction"][
First@DSolve[Join[eqny, icvy], y, t]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/65f8951b385c9edd.png)
![ResourceFunction["SymbolToSubscript"][
ResourceFunction["FullSimplifyFunction"][
First@DSolve[Join[eqn\[Theta], icv\[Theta]], \[Theta], t]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/19736daa85c43f35.png)
![b = 1;
c = 2;
Block[{b}, ResourceFunction["FullSimplifyFunction"][
Function[x, c^2 x^2 + 2 b c x + b^2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8db/8dbffec2-4279-4c31-8edf-c20dc5638659/4bf78ed0c8090c48.png)