Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SchurMatrix

Source Notebook

Generate the Schur matrix of a univariate polynomial

Contributed by: Jan Mangaldan

ResourceFunction["SchurMatrix"][poly,x]

gives the Schur matrix of poly, treated as a polynomial in x.

Details

The Schur matrix is also called the Schur-Cohn matrix or Schur-Cohn-Fujiwara matrix.
The Schur matrix is a matrix constructed from the coefficients of a polynomial, and can be used to check if the polynomial's roots are all within the unit disk.
The Schur matrix is a Hermitian matrix.
In control theory, a polynomial is stable if all of its roots are within the unit disk. A polynomial is stable if and only if its Schur matrix is positive definite.

Examples

Basic Examples (1) 

Generate the Schur matrix of a polynomial:

In[1]:=
ResourceFunction["SchurMatrix"][5 + 4 x + 3 x^2 + 2 x^3 + x^4 + x^5, x] // MatrixForm
Out[1]=

Scope (3) 

Generate the Schur matrix from a polynomial with numeric coefficients:

In[2]:=
ResourceFunction["SchurMatrix"][2 x^6 - 5 x^5 - 3 x + 9, x] // MatrixForm
Out[2]=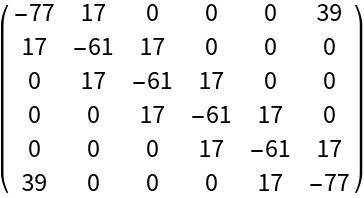

Generate the Schur matrix from a polynomial with symbolic coefficients:

In[3]:=
ResourceFunction["SchurMatrix"][\!\( \*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(3\)]\(\* TemplateBox[{"k"}, "C"] \*SuperscriptBox[\(x\), \(k\)]\)\), x] // Simplify // MatrixForm
Out[3]=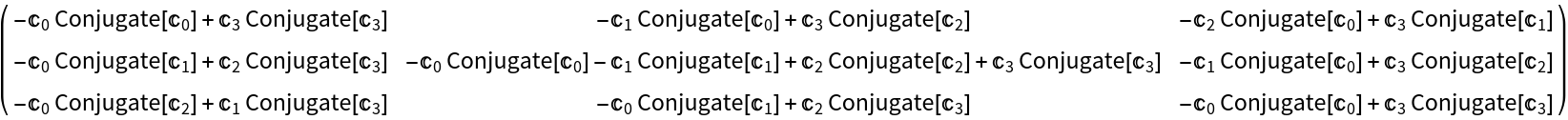

The Schur matrix for a cyclotomic polynomial is the zero matrix:

In[4]:=
ResourceFunction["SchurMatrix"][Cyclotomic[11, x], x]
Out[4]=

Applications (2) 

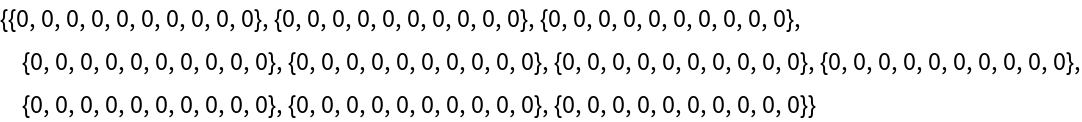Use SchurMatrix to check the stability of a polynomial:

In[5]:=
poly = 5 x^4 + 4 x^3 + 3 x^2 + 2 x + 1; MatrixForm[ma = ResourceFunction["SchurMatrix"][poly, x]]
Out[6]=
In[7]:=
PositiveDefiniteMatrixQ[ma]
Out[7]=

Verify stability by computing the roots of the polynomial:

In[8]:=
Abs[x] < 1 /. NSolve[poly == 0, x]
Out[8]=

The Schur matrix of a quadratic polynomial with symbolic coefficients:

In[9]:=
ma = ResourceFunction["SchurMatrix"][a z^2 + b z + c, z]
Out[9]=

Use the resource function RationalCholeskyDecomposition to transform the Schur matrix into a congruent diagonal matrix:

In[10]:=
diag = Simplify[ Last[ResourceFunction["RationalCholeskyDecomposition"][ma]]]
Out[10]=

Determine the conditions for the Schur matrix to be positive definite (which is equivalent to the original polynomial being stable):

In[11]:=
Reduce[Apply[And, Thread[diag > 0]], {a, b, c}] // FullSimplify
Out[11]=

Properties and Relations (2) 

The Schur matrix is Hermitian:

In[12]:=
ma = ResourceFunction["SchurMatrix"][z^3 - (1 + 2 I) z + 3, z]
Out[12]=
In[13]:=
HermitianMatrixQ[ma]
Out[13]=

The inverse of a Schur matrix is a Toeplitz matrix:

In[14]:=
Inverse[ma] // MatrixForm
Out[14]=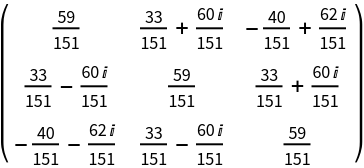

A polynomial whose roots are all inside the unit disk:

In[15]:=
poly[z_] := 5 z^4 + 4 z^3 + 3 z^2 + 2 z + 1

The corresponding Schur matrix is positive definite:

In[16]:=
ResourceFunction["SchurMatrix"][poly[z], z] // PositiveDefiniteMatrixQ
Out[16]=

Apply a Möbius transformation to the polynomial:

In[17]:=
polyMoebius[z_] = Collect[Together[(z - 1)^Exponent[poly[z], z] poly[(z + 1)/(z - 1)]], z, Simplify]
Out[17]=

The transformed polynomial has a Hurwitz matrix whose principal minors are all positive. That is, all of the roots of the transformed polynomial have negative real parts:

In[18]:=
ma = ResourceFunction["HurwitzMatrix"][polyMoebius[z], z]; Table[Det[Take[ma, k, k]] > 0, {k, Exponent[polyMoebius[z], z]}]
Out[19]=

Version History

  • 1.0.0 – 27 March 2023

Source Metadata

  • Citation:
    • Bistritz Y., "Reflections on Schur-Cohn matrices and Jury-Marden tables and classification of related unit circle zero location criteria." Circuits, Systems and Signal Processing, vol. 15, no. 1, 111–136, 1996.
      DOI: 10.1007/BF01187696
    • Hinrichsen D., Pritchard A.J., Mathematical Systems Theory I: Modelling, State Space Analysis, Stability and Robustness. Berlin: Springer-Verlag, 347–350, 2005.
    • Viera A., Kailath T., "On another approach to the Schur-Cohn criterion." IEEE Transactions on Circuits and Systems, vol. 24, no. 4, 218–220, 1977.
      DOI: 10.1109/TCS.1977.1084319

Related Resources

License Information