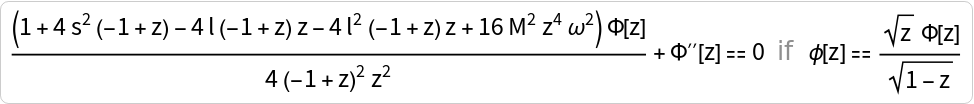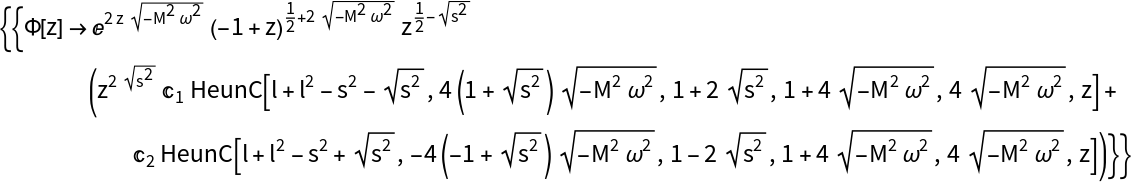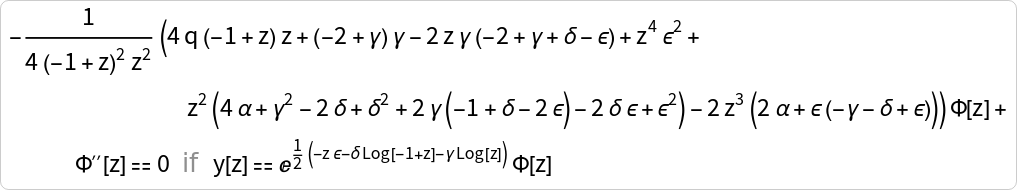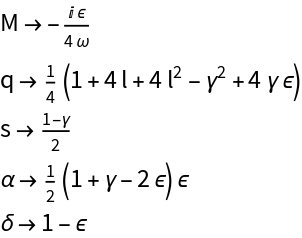Basic Examples (3)
Transform an ODE into normal form:
The second argument allows one to specify a new symbol for the new dependent variable:
The transformation of the dependent variable is obtained by applying Last:
Scope (4)
The normal form can be obtained for equations of any order:
The equation is automatically simplified:
Apply the function to a non-linear equation:
If the equation is already in normal form, the function still simplifies it:
Options (3)
Let us consider the Appell equation:
In normal form, by default it becomes a cumbersome expression:
This result can be further simplified through the option "SimplifyEquation":
Properties and Relations (4)
We can check that the solution of the differential equation in the original form:
and in normal form:
are mapped into each other by the dependent variable transformation:
However, this cannot be immediately verified in all cases, since the linear combination of solutions may be chosen differently:
Possible Issues (2)
For the moment, ODENormalForm works only for single variable (aka ordinary) linear differential equations:
It can deal with some non-linear equations, but not in their leading or sub-leading coefficient:
Neat Examples (5)
Let us consider the Regge-Wheeler (RW) equation, governing axial perturbations of black holes:
As it is written, we can find its solution only in the unintuitive DifferentialRoot form:
Let us try to transform this equation into normal form (and change independent variable as ), simply as:
Now, we can better find its solution in terms of the HeunC function:
Let us also map the black hole parameters into the Confluent Heun ones, by transforming the latter equation into normal form:
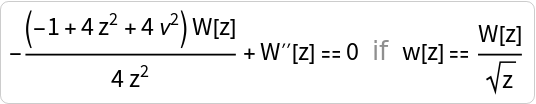
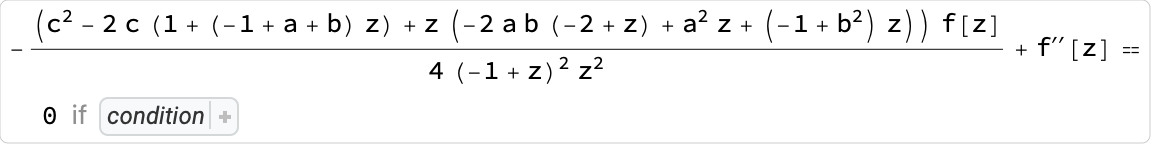

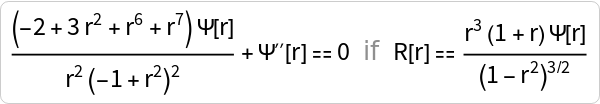
![appelODE = MathematicalFunctionData["AppellF1", "DifferentialEquations"][[2, 2, 1, 1]] // ToExpression@
StringReplace[ToString@FullForm[#], "\\[Formal" ~~ x_ ~~ "]" :> ToLowerCase[x]] &](https://www.wolframcloud.com/obj/resourcesystem/images/7d0/7d0d6a97-398f-46a6-a2b3-0157a66a15df/25667bb98e454338.png)
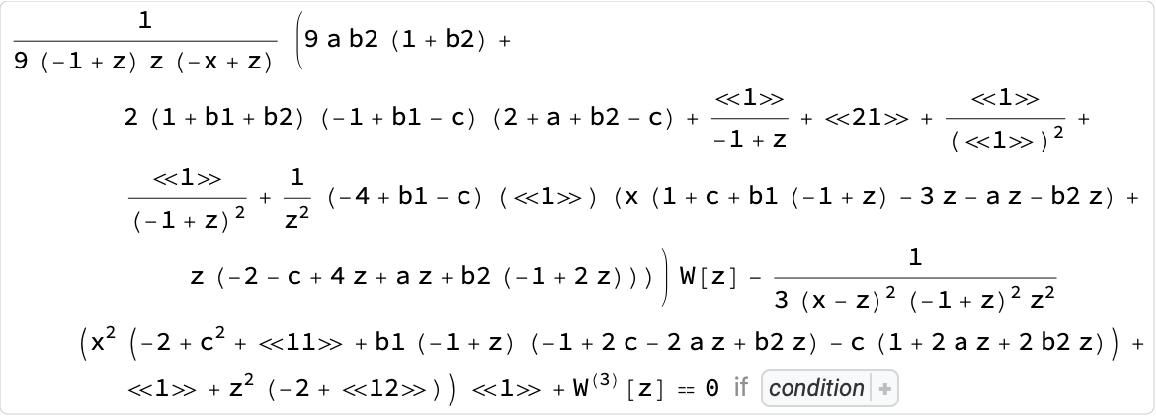



![rwODE = With[{f = 1 - 2 M/# &}, f[r] D[f[r] D[#, r], r] &@\[Phi][r] + \[Omega]^2 \[Phi][r] - f[r] ((l (l + 1))/r^2 + (1 - s^2) (2 M)/r^3) \[Phi][r] == 0]](https://www.wolframcloud.com/obj/resourcesystem/images/7d0/7d0d6a97-398f-46a6-a2b3-0157a66a15df/082f6b73a16a8291.png)
![rwODENormal = ResourceFunction["ODENormalForm"][
First@DSolveChangeVariables[
Inactive[DSolve][rwODE, \[Phi][r], r], \[Phi][z], z, r == 2 M z]]](https://www.wolframcloud.com/obj/resourcesystem/images/7d0/7d0d6a97-398f-46a6-a2b3-0157a66a15df/20c3746afa4ec36b.png)