Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Sample a product distribution pseudo randomly in a way that guarantees good coverage of all marginals
ResourceFunction["LatinHypercubeSample"][dim,n] generates n hypercube samples from ProductDistribution[{UniformDistribution[],dim}]. | |
ResourceFunction["LatinHypercubeSample"][dist,n] generates n samples from dist that cover the probability space of the distribution equally. | |
ResourceFunction["LatinHypercubeSample"][{dist1,dist2,…},n] generates n hypercube samples from ProductDistribution[dist1,dist2,…]. | |
ResourceFunction["LatinHypercubeSample"][spec, n, m] repeats the sampling m times, generating n×m samples. |
| In[1]:= | ![\!\(\*
GraphicsBox[
RasterBox[SparseArray[
Automatic, {5, 5}, 1., {1, {{0, 1, 2, 3, 4, 5}, {{1}, {3}, {5}, {4}, {2}}}, {0., 0.,
0., 0., 0.}}], {{0, 0}, {5, 5}}, {0, 1}],
Frame->Automatic,
FrameLabel->{None, None},
FrameTicks->{{None, None}, {None, None}},
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]],
ImageSize->{178.5, Automatic},
Method->{"GridLinesInFront" -> True, "DefaultBoundaryStyle" -> Automatic, "DefaultGraphicsInteraction" -> {"Version" -> 1.2, "TrackMousePosition" -> {True, False}, "Effects" -> {"Highlight" -> {"ratio" -> 2}, "HighlightPoint" -> {"ratio" -> 2}, "Droplines" -> {"freeformCursorMode" -> True, "placement" -> {"x" -> "All", "y" -> "None"}}}}, "DefaultPlotStyle" -> Automatic}]\)](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7abf1a74-c511-44bf-936c-4e3c32869893/43e4d6ec20230b77.png) |
Generate 10 random numbers between 0 and 1 that are roughly equally spaced:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
In the case of 10 samples, each leading digit will always get exactly one sample:
| In[3]:= |
| Out[3]= |
Repeat the sampling 10 times to generate 100 samples:
| In[4]:= |
| Out[4]= |
Generate pairs of uniformly distributed numbers on the unit square:
| In[5]:= |
| Out[5]= | 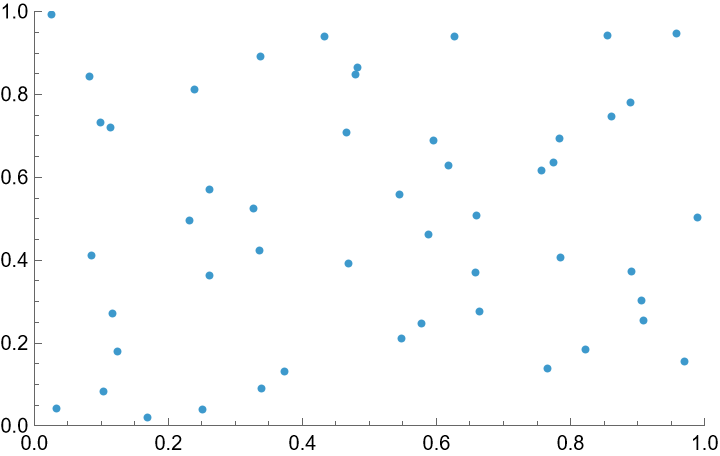 |
Generate 10 samples from NormalDistribution[] that are equally distributed in probability space:
| In[6]:= |
| Out[6]= |
Demonstrate the equal spacing:
| In[7]:= |
| Out[7]= |
Due the use of equal spacing of the selection regions, samples tend to align more closely to the reference distribution in a ProbabilityPlot than completely random samples:
| In[8]:= | ![ProbabilityPlot[{normalLHCSamples, RandomVariate[NormalDistribution[], 10]}, NormalDistribution[]]](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7abf1a74-c511-44bf-936c-4e3c32869893/5b79f7d2c9f309a9.png) |
| Out[8]= | 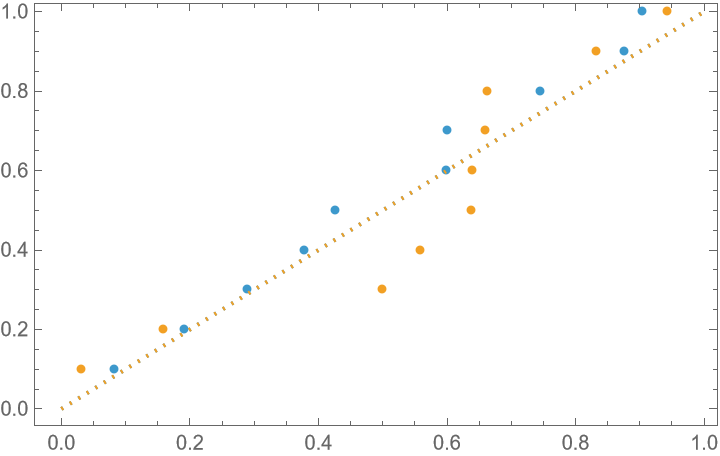 |
Sample a product of multiple different distributions, continuous or discrete:
| In[9]:= | ![ResourceFunction[
"LatinHypercubeSample"][{NormalDistribution[], ExponentialDistribution[5], PoissonDistribution[2]}, 10, 5] // Tabular](https://www.wolframcloud.com/obj/resourcesystem/images/7ab/7abf1a74-c511-44bf-936c-4e3c32869893/39555d63a2a4db5d.png) |
| Out[9]= | 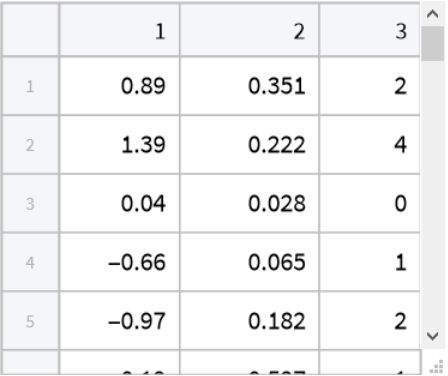 |
Generate discrete samples from 1 to n:
| In[10]:= |
| Out[11]= |
Each row and each column has exactly one sample:
| In[12]:= |
| Out[12]= |  |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License