Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ClickPoincarePlot2D

Source Notebook

Create an interactive view of Poincaré sections of a two-degree-of-freedom Hamiltonian system

Contributed by: E. Chan-López, Héctor Argote Morales, Wojciech Szumiński & Víctor Castellanos

ResourceFunction["ClickPoincarePlot2D"][odes,h,energy,time,timemax,cross,recover]

gives the Poincaré sections corresponding to the differential equations represented by odes, the Hamiltonian h, the energy level energy, the time variable time, the maximum time of evolution timemax, the intersection cross and the section recover, with initial conditions determined by clicking within an interactive panel.

Details and Options

Formally, in classical mechanics, the Hamiltonian is a mathematical function that describes the total energy (kinetic and potential energies) of a physical system, considering all interactions between its constituents. It is denoted by H and is defined in terms of the coordinates and generalized momenta of the system.
The temporal evolution of the Hamiltonian system is governed by Hamilton's equations. These equations arise from the Hamiltonian function using the Poisson Bracket.
Formally, a Hamiltonian system refers to a physical system described within the framework of Hamiltonian mechanics. In this approach, the system is characterized by its phase space, which is an abstract space where each point represents a set of generalized coordinates and their corresponding conjugate momenta.
The odes must be a list of ordinary differential equations, specifically a Hamiltonian system.
The h must be a Hamiltonian function.
The energy must be a numeric expression. The variable energy represents the energy level chosen when painting a Poincaré section. It is a parameter that determines the specific energy value at which the section is taken. By selecting different values of energy, one can explore different energy regimes and capture distinct features of the dynamical system on the Poincaré section.
The cross should be a time-dependent variable. It can also be an equation, where its left-hand side is a time-dependent variable and its right-hand side is a constant. The argument cross represents the crossing plane of the solutions.
The recover must be a list of two time-dependent variables. This list indicates the plane where the points of each section will be collected.
ResourceFunction["ClickPoincarePlot2D"][odes,h,energy,time,timemax,cross,recover] collects the data of the initial value together with the data of the associated orbit, this depending on the points that the user chooses in the clickable panel, also drawing the respective section.
ResourceFunction["ClickPoincarePlot2D"][odes,h,energy,time,timemax,cross,recover] takes the same options as ListPlot.

Examples

Basic Examples (1) 

Generate a Poincaré section of the following system:

In[1]:=
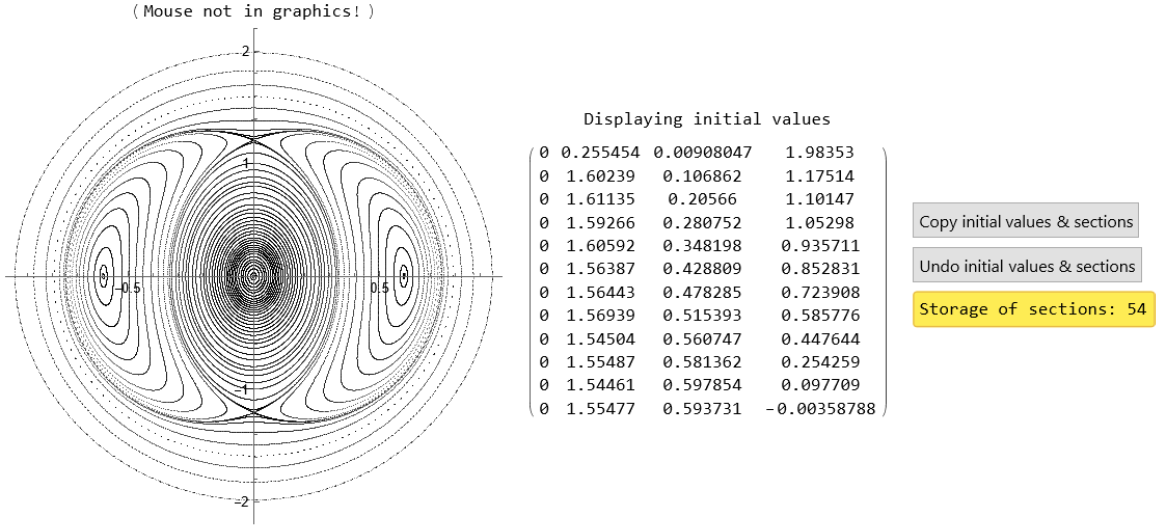
H := Function[{S}, 1/2 (S[[2]]^2 + S[[4]]^2 + S[[1]]^2 + S[[3]]^2) + 2*S[[1]]^2 S[[3]]] eq1 = x'[t] == px[t]; eq2 = px'[t] == -x[t] (1 + 2 y[t]); eq3 = y'[t] == py[t]; eq4 = py'[t] == -x[t]^2 - y[t];
In[2]:=
ResourceFunction[ "ClickPoincarePlot2D"][{eq1, eq2, eq3, eq4}, H, 0.012, t, 5000, x[t], {y[t], py[t]}, {PlotStyle -> {{ AbsolutePointSize[1], GrayLevel[0], Opacity[0.4]}}, AspectRatio -> 1, PlotHighlighting -> None}]
Out[2]=

Applications (5) 

Chaotic regime in the Hénon-Heiles Equation (1) 

Generate Poincaré sections of the Hénon-Heiles Equation under chaotic regime:

In[3]:=
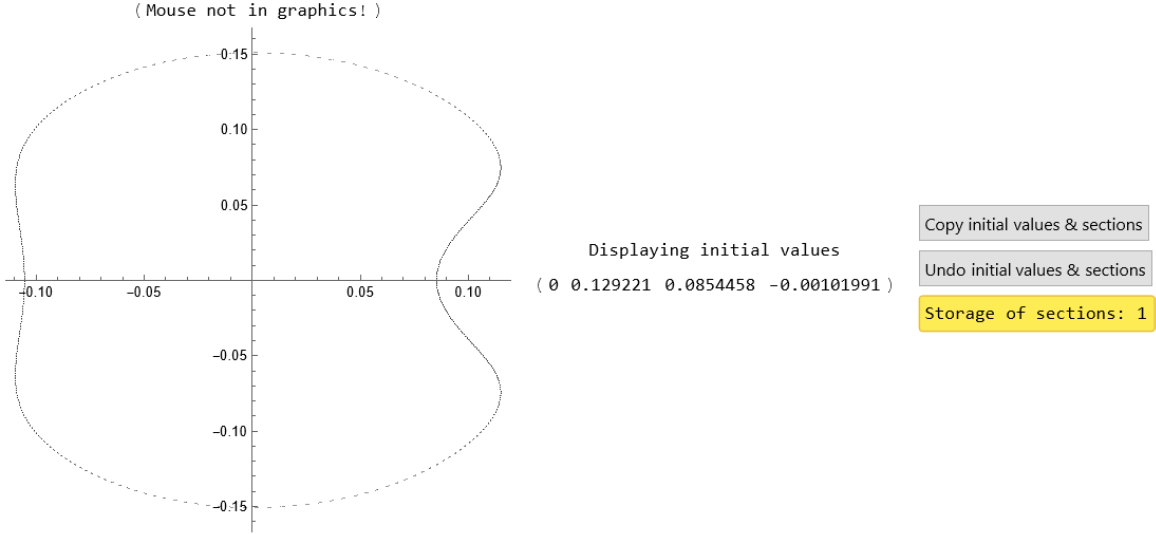
H := Function[{S}, 1/2 (S[[2]]^2 + S[[4]]^2 + S[[1]]^2 + S[[3]]^2) + S[[1]]^2 S[[3]] - 1/3 S[[3]]^3] eq1 = x'[t] == px[t]; eq2 = px'[t] == -(x[t] + 2 x[t]* y[t]); eq3 = y'[t] == py[t]; eq4 = py'[t] == -(y[t] + x[t]^2 - y[t]^2);
In[4]:=
ResourceFunction[ "ClickPoincarePlot2D"][{eq1, eq2, eq3, eq4}, H, 0.1173, t, 6000, x[t], {y[t], py[t]}, {PlotStyle -> {{ AbsolutePointSize[1], GrayLevel[0], Opacity[0.4]}}, AspectRatio -> 1, PlotHighlighting -> None}]
Out[4]=

The swing-spring (1) 

Generate the Poincaré sections of the swing-spring:

In[5]:=
H := Function[{S}, 1/2 (S[[2]]^2 + S[[4]]^2) + S[[3]] + 2 (3/4 - Sqrt[S[[1]]^2 + (S[[3]] - 1)^2])^2 - 1/8] eq1 = x'[t] == px[t]; eq2 = px'[t] == x[t] (-4 + 3/Sqrt[x[t]^2 + (-1 + z[t])^2]); eq3 = z'[t] == pz[t]; eq4 = pz'[t] == 3 - 3/Sqrt[ x[t]^2 + (-1 + z[t])^2] + (-4 + 3/Sqrt[x[t]^2 + (-1 + z[t])^2]) z[ t]; hameqns = {eq1, eq2, eq3, eq4}; cross = x[t]; recover = {z[t], pz[t]};
In[6]:=
ResourceFunction[ "ClickPoincarePlot2D"][hameqns, H, 0.84, t, 6000, cross, recover, {PlotStyle -> AbsolutePointSize[1], AspectRatio -> 1, PlotHighlighting -> None}]
Out[6]=

Relativistic anisotropic harmonic oscillator (1) 

Generate the Poincaré sections of the relativistic anisotropic harmonic oscillator:

In[7]:=
Clear[H, eq1, eq2, eq3, eq4, hameqns, cross, recover]
In[8]:=
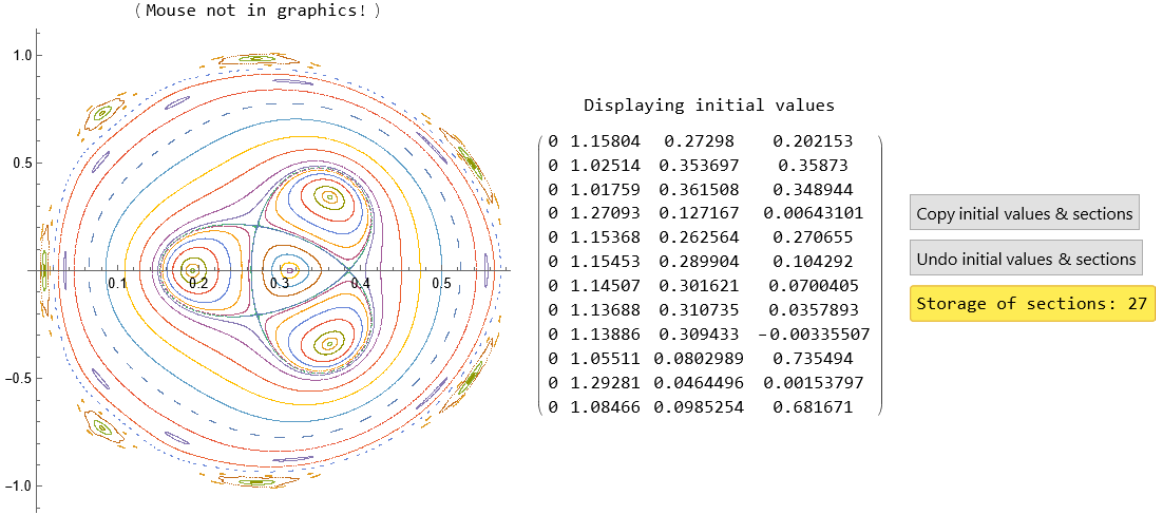
H := Function[{S}, Sqrt[1 + S[[2]]^2 + S[[4]]^2] + S[[1]]^2/2 + S[[3]]^2/2 + S[[3]]^4/ 80] eq1 = Derivative[1][x][t] == px[t]/Sqrt[1 + px[t]^2 + py[t]^2]; eq2 = Derivative[1][px][t] == -x[t]; eq3 = Derivative[1][y][t] == py[t]/Sqrt[1 + px[t]^2 + py[t]^2]; eq4 = Derivative[1][py][t] == -y[t] - y[t]^3/20; hameqns = {eq1, eq2, eq3, eq4}; cross = y[t]; recover = {x[t], px[t]};
In[9]:=
ResourceFunction[ "ClickPoincarePlot2D"][hameqns, H, 90, t, 6000, cross, recover, {PlotStyle -> {{ AbsolutePointSize[1], GrayLevel[0], Opacity[0.4]}}, AspectRatio -> 1, PlotHighlighting -> None}]
Out[9]=

The galactic model of Contopoulos (1) 

Generate the Poincaré sections for the Contopoulos model:

In[10]:=
Clear[H, eq1, eq2, eq3, eq4, hameqns, cross, recover]
In[11]:=
H := Function[{S}, S[[2]]^2/2 + S[[4]]^2/(2 Sqrt[2]) + S[[3]]^2/(2 Sqrt[2]) - S[[3]]^3/ 3 + S[[1]]^2 (1/2 + S[[3]])] eq1 = x1'[t] == px1[t]; eq2 = px1'[t] == -x1[t] (1 + 2 x2[t]); eq3 = x2'[t] == px2[t]/Sqrt[2]; eq4 = px2'[t] == -x1[t]^2 - (1/Sqrt[2] - x2[t]) x2[t]; hameqns = {eq1, eq2, eq3, eq4}; cross = x1[t]; recover = {x2[t], px2[t]};
In[12]:=
ResourceFunction[ "ClickPoincarePlot2D"][hameqns, H, 0.052, t, 6000, cross, recover, {PlotStyle -> AbsolutePointSize[1], AspectRatio -> 1, PlotHighlighting -> None}]
Out[12]=

Rydberg hydrogen atom near a metallic surface (1) 

Generate the Poincaré sections for the Rydberg hydrogen atom near a metallic surface:

In[13]:=
Clear[H, eq1, eq2, eq3, eq4, hameqns, cross, recover]
In[14]:=
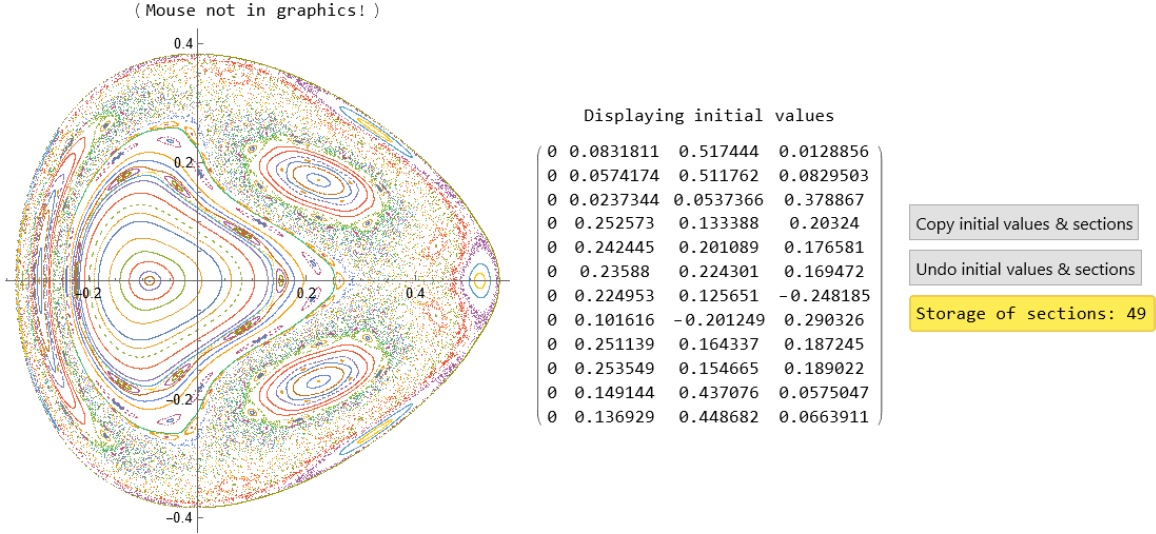
\[Xi] = -2; H := Function[{S}, 1/2 (S[[2]]^2 + S[[4]]^2) - \[Xi] (S[[1]]^2 + S[[3]]^2) - ( S[[1]]^2 + S[[3]]^2)/(2 (2 + S[[1]]^2 - S[[3]]^2)) + ( 2 (S[[1]]^2 + S[[3]]^2))/Sqrt[ 4 S[[1]]^2 S[[3]]^2 + (4 + (S[[1]]^2 - S[[3]]^2))^2]] eq1 = u'[t] == pu[t]; eq2 = pu'[t] == u[t] (2 \[Xi] - (2 (-1 + v[t]^2))/(2 + u[t]^2 - v[t]^2)^2 - ( 16 (4 + u[t]^2 - 3 v[t]^2))/(u[t]^4 + (-4 + v[t]^2)^2 + 2 u[t]^2 (4 + v[t]^2))^(3/2)); eq3 = v'[t] == pv[t]; eq4 = pv'[t] == v[t] (2 \[Xi] + (2 (1 + u[t]^2))/(2 + u[t]^2 - v[t]^2)^2 - ( 16 (4 + 3 u[t]^2 - v[t]^2))/(u[t]^4 + (-4 + v[t]^2)^2 + 2 u[t]^2 (4 + v[t]^2))^(3/2)); hameqns = {eq1, eq2, eq3, eq4}; cross = u[t]; recover = {v[t], pv[t]};
In[15]:=
ResourceFunction[ "ClickPoincarePlot2D"][hameqns, H, 2, t, 3000, cross, recover, {PlotStyle -> {{ AbsolutePointSize[1], GrayLevel[0], Opacity[0.4]}}, AspectRatio -> 1, PlotHighlighting -> None}]
Out[15]=

Publisher

Ramón Eduardo Chan López

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.1 – 02 October 2023
  • 1.0.0 – 13 July 2023

Source Metadata

  • Citation:
    • Lowenstein, J. H. (2012). Essentials of Hamiltonian dynamics. Cambridge University Press. DOI: 10.1017/CBO9780511793721
    • van der Weele, J. P., & de Kleine, E. (1996). The order—chaos—order sequence in the spring pendulum. Physica A: Statistical Mechanics and its Applications, 228(1-4), 245-272. DOI: 10.1016/0378-4371(95)00426-2
    • Vieira, R. S., & Michtchenko, T. A. (2018). Relativistic chaos in the anisotropic harmonic oscillator. Chaos, Solitons & Fractals, 117, 276-282. DOI: 10.1016/j.chaos.2018.10.027
    • Giorgilli, A. (2022). Notes on Hamiltonian Dynamical Systems (Vol. 102). Cambridge University Press. DOI: 10.1017/9781009151122
    • Iñarrea, M., Lanchares, V., Palacián, J. F., Pascual, A. I., Salas, J. P., & Yanguas, P. (2007). Rydberg hydrogen atom near a metallic surface: Stark regime and ionization dynamics. Physical Review A, 76(5), 052903. DOI: 10.1103/PhysRevA.76.052903

Related Resources

License Information