Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the integral describing the area between two plane curves
ResourceFunction["AreaBetweenCurvesIntegral"][{f,g},{x,xmin,xmax}] returns an Inactive integral representing the area of the enclosed region between the functions f(x) and g(x) over the interval xmin<x<xmax. |
| Assumptions | $Assumptions | assumptions on parameters |
Compute an integral representing the area between two curves:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 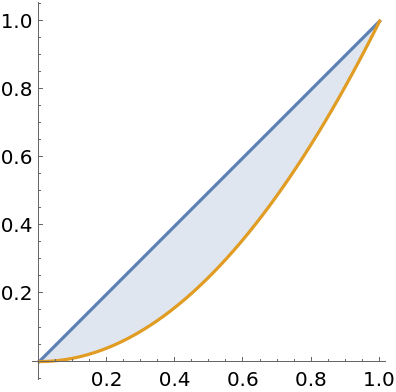 |
Activate the integral to compute the area:
| In[3]:= |
| Out[3]= |
Find the area of the region enclosed by two curves:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= | 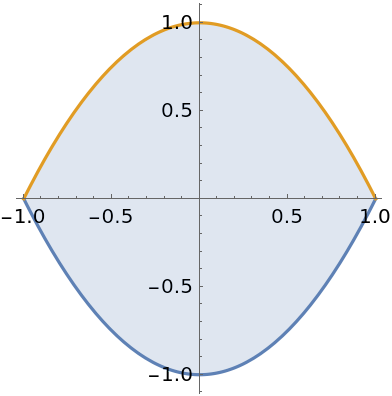 |
Where the curves do not meet:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= | 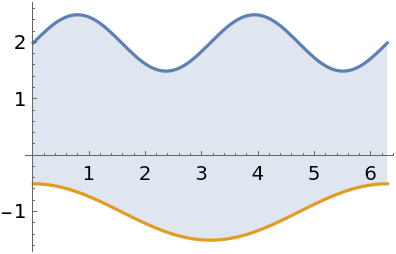 |
With multiple enclosed regions, the integrand will use Abs to return a positive area:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 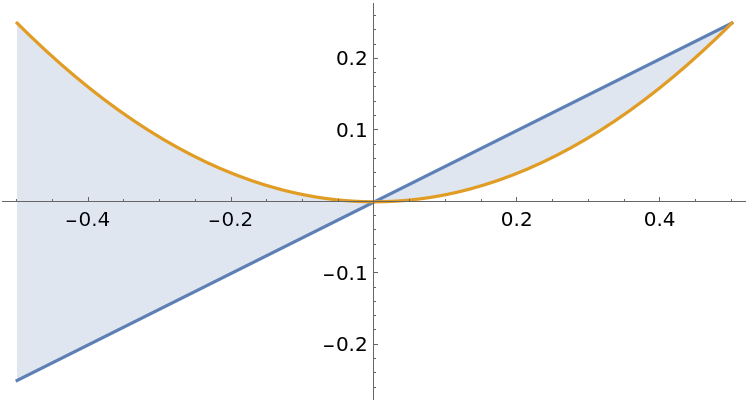 |
Between curves containing parameters:
| In[11]:= |
| Out[11]= |
The result may be conditioned on parameters:
| In[12]:= |
| Out[12]= | 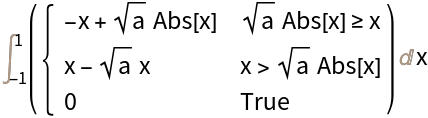 |
Make an assumption about the parameter to then evaluate the area:
| In[13]:= |
| Out[13]= | 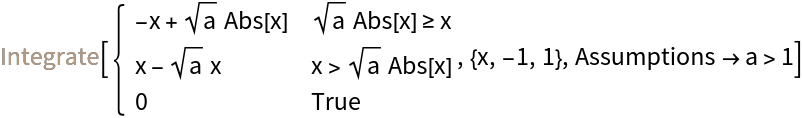 |
| In[14]:= |
| Out[14]= |
Compute the area of a disk:
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= | 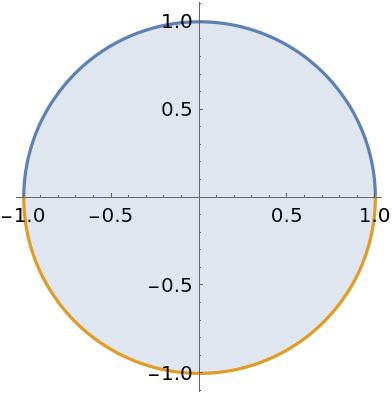 |
Cavalieri's principle states that the area between two curves does not change when each curve is shifted by the same amount:
| In[18]:= |
| In[19]:= |
| In[20]:= |
| Out[20]= |
| In[21]:= |
| Out[21]= |
| In[22]:= |
| Out[22]= | 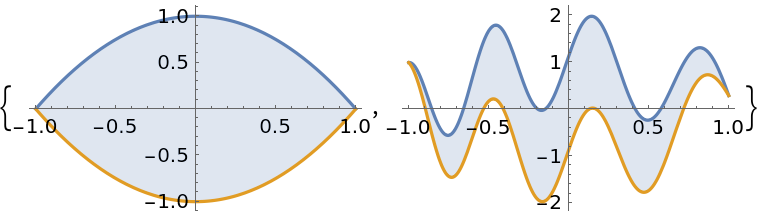 |
Use resource function AreaBetweenCurves to compute the area directly:
| In[23]:= |
| Out[23]= |
This work is licensed under a Creative Commons Attribution 4.0 International License