Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert a unit quaternion to an equivalent rotation matrix
ResourceFunction["QuaternionToRotationMatrix"][w] converts the unit quaternion w into an equivalent 3×3 rotation matrix. |
Define a quaternion:
| In[1]:= |
| Out[1]= |
Generate a rotation matrix from a unit quaternion:
| In[2]:= |
| Out[2]= | 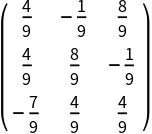 |
Verify that the result is a rotation matrix:
| In[3]:= |
| Out[3]= |
An exact quaternion:
| In[4]:= |
| Out[4]= |  |
An approximate MachinePrecision quaternion:
| In[5]:= |
| Out[5]= |
An approximate arbitrary precision quaternion:
| In[6]:= |
| Out[6]= |
QuaternionToRotationMatrix threads over lists:
| In[7]:= |
| Out[7]= |
Create a unit quaternion:
| In[8]:= |
| Out[8]= |
Also define a vector to be rotated:
| In[9]:= |
| Out[9]= |
Transform the vector using the quaternion representation of a rotation:
| In[10]:= |
| Out[10]= |
Transform the vector using the rotation matrix representation to get the same result:
| In[11]:= |
| Out[11]= |
Get the axis-angle representation of a quaternion:
| In[12]:= | ![ResourceFunction["AxisAngle"][
ResourceFunction["QuaternionToRotationMatrix"][
ResourceFunction["Quaternion"][2/9, 5/9, 2/3, 4/9]]]](https://www.wolframcloud.com/obj/resourcesystem/images/754/75487094-1ad3-490d-9d43-70ef1de35fd7/4d3caef4219de797.png) |
| Out[12]= |
Recover the original quaternion:
| In[13]:= |
| Out[13]= |
Create the icosians, a set of quaternions equivalent to the vertices of the 4D 600-cell:
| In[14]:= | ![quads = {{2, 0, 0, 0}, {1, 1, 1, 1}, {0, 1, 1/\[Phi], \[Phi]}}/
2 /. \[Phi] -> (1 + Sqrt[5])/2; cell120 = Flatten[ResourceFunction["SignedPermutations"][#, "Even"] & /@ quads, 1];
icosians = SortBy[ResourceFunction["Quaternion"] @@ # & /@ cell120, Sort[{#, Conjugate[#]}] &];](https://www.wolframcloud.com/obj/resourcesystem/images/754/75487094-1ad3-490d-9d43-70ef1de35fd7/0d4d0dd5bc610c37.png) |
Use the icosians to generate the 120 rotation matrices in the icosahedral group:
| In[15]:= | ![all = RootReduce[
Table[If[OddQ[k], -1, 1]*
ResourceFunction["QuaternionToRotationMatrix"][
icosians[[k]]], {k, 1, 120}]];](https://www.wolframcloud.com/obj/resourcesystem/images/754/75487094-1ad3-490d-9d43-70ef1de35fd7/455a69c9074f5766.png) |
Use the 120 rotation matrices and one triangle of the disdyakis triacontahedron to build the full figure:
| In[16]:= | ![tri = {{1/2 (-1 + Sqrt[5]), 0, 1/2 (1 + Sqrt[5])}, {0, 1, 1/2 (1 + Sqrt[5])}, {0, 0, 1/22 (5 + 15 Sqrt[5])}}; Graphics3D[{Polygon[tri . #] & /@ all}, SphericalRegion -> True, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/754/75487094-1ad3-490d-9d43-70ef1de35fd7/6688c9016140819c.png) |
| Out[16]= | 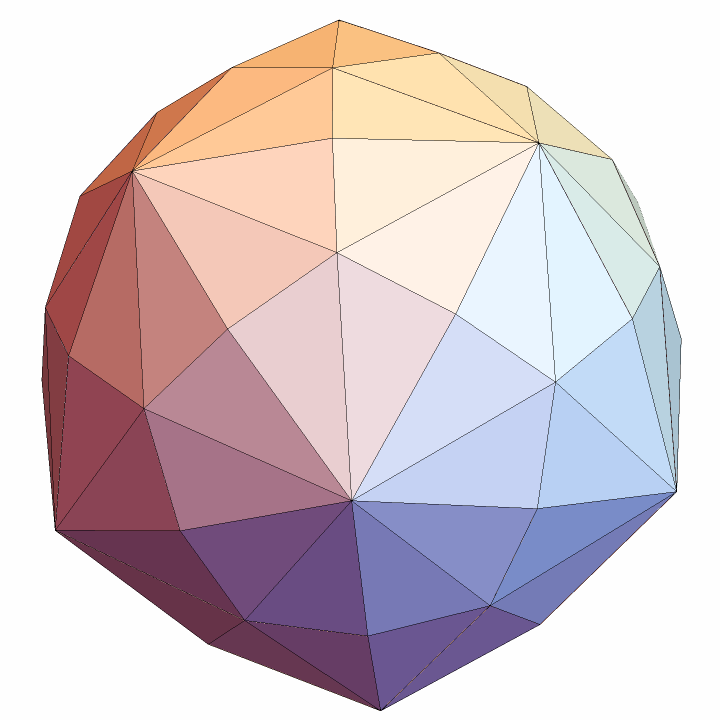 |
This work is licensed under a Creative Commons Attribution 4.0 International License