Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Visualize the evolution of a one-dimensional neighbor-independent substitution system
ResourceFunction["SubstitutionSystemPlot"][rule,init,t] visualizes the evolution of the list substitution system with the specified rule from initial condition init for t steps. | |
ResourceFunction["SubstitutionSystemPlot"][rule,init,{t1,t2}] visualizes the evolution from steps t1 through t2. |
| Alignment | Center | alignment of the boxes used to visualize the steps |
| Appearance | Automatic | overall appearance |
| ColorRules | Automatic | rules for determining colors from values |
| Mesh | Automatic | whether to draw a mesh |
| MeshStyle | Automatic | the style to use for a mesh |
| Offset | Automatic | offsets for the boxes used to visualize the steps |
Show five steps of a string substitution system:
| In[1]:= |
| Out[1]= | 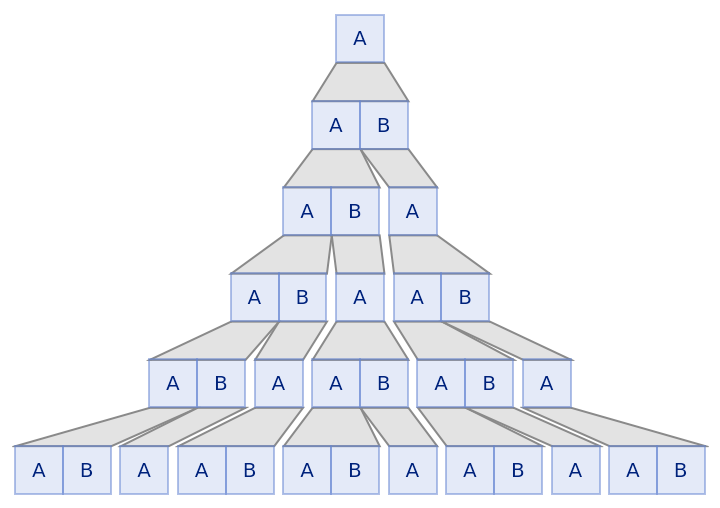 |
Show as an array:
| In[2]:= |
| Out[2]= | 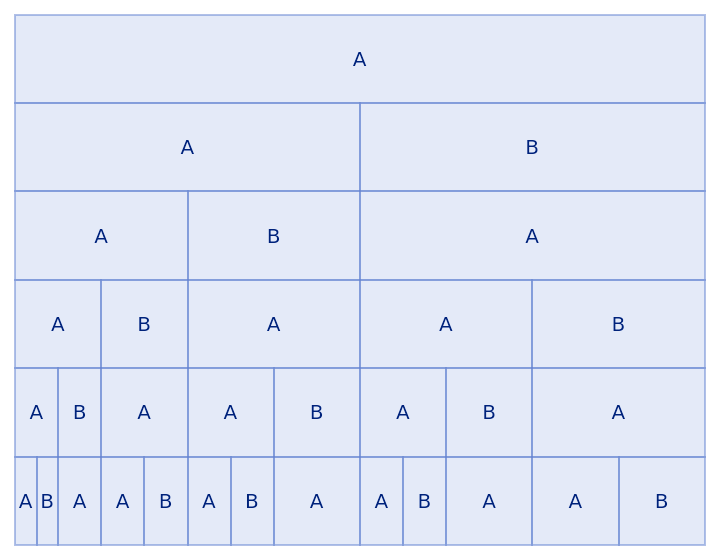 |
Show only the second to fourth steps:
| In[3]:= |
| Out[3]= | 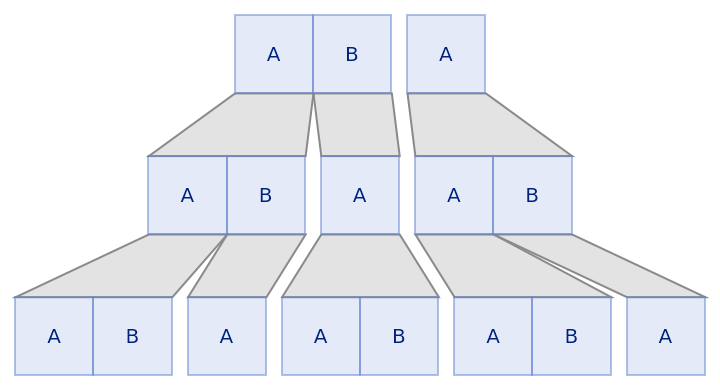 |
Show the second to fourth steps as an array:
| In[4]:= |
| Out[4]= | 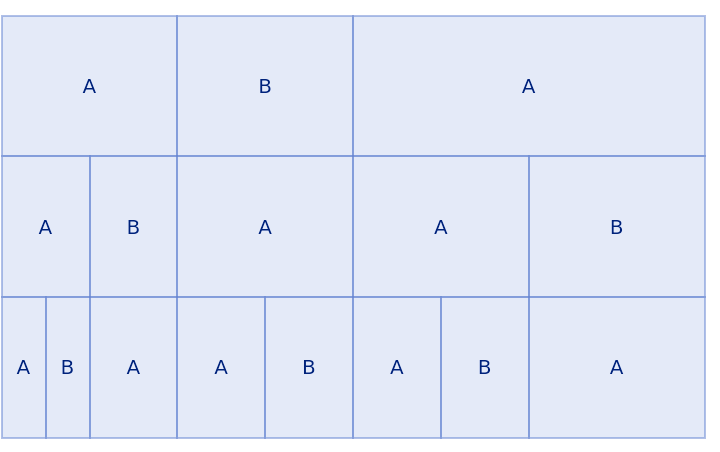 |
Show only the first step:
| In[5]:= |
| Out[5]= | 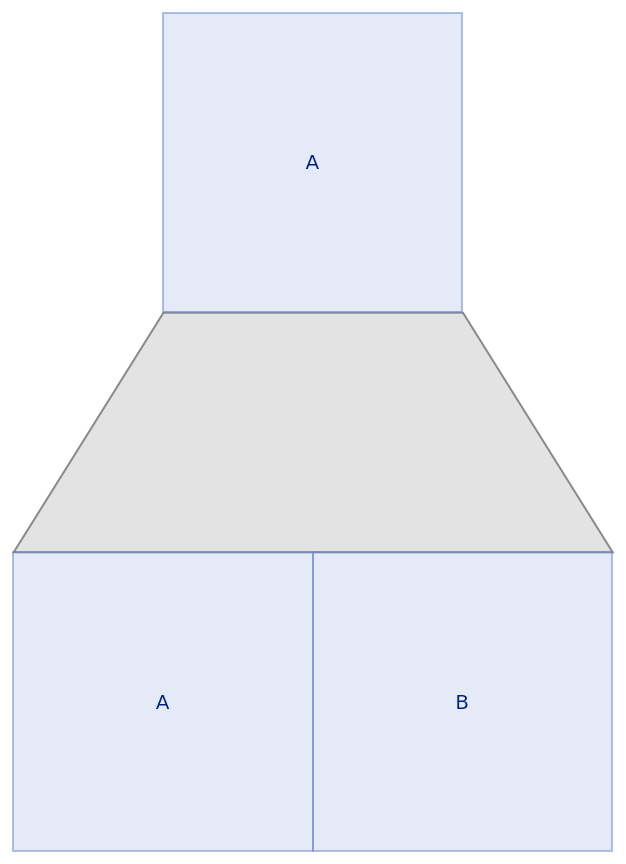 |
Show the first step as an array:
| In[6]:= |
| Out[6]= | 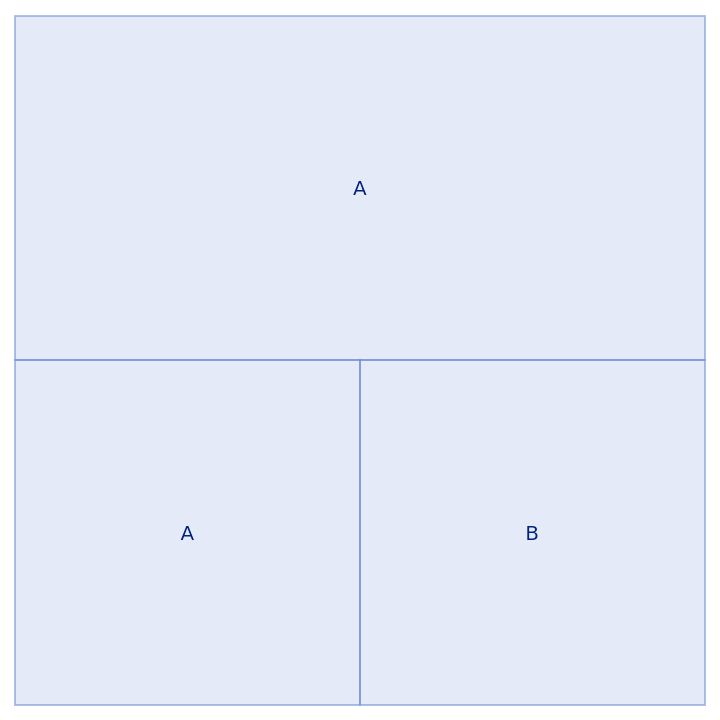 |
Use any symbol:
| In[7]:= |
| Out[7]= |  |
| In[8]:= |
| Out[8]= | 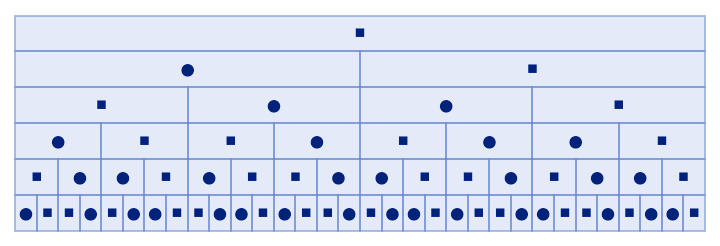 |
Lists do not have to be the same length:
| In[9]:= |
| Out[9]= | 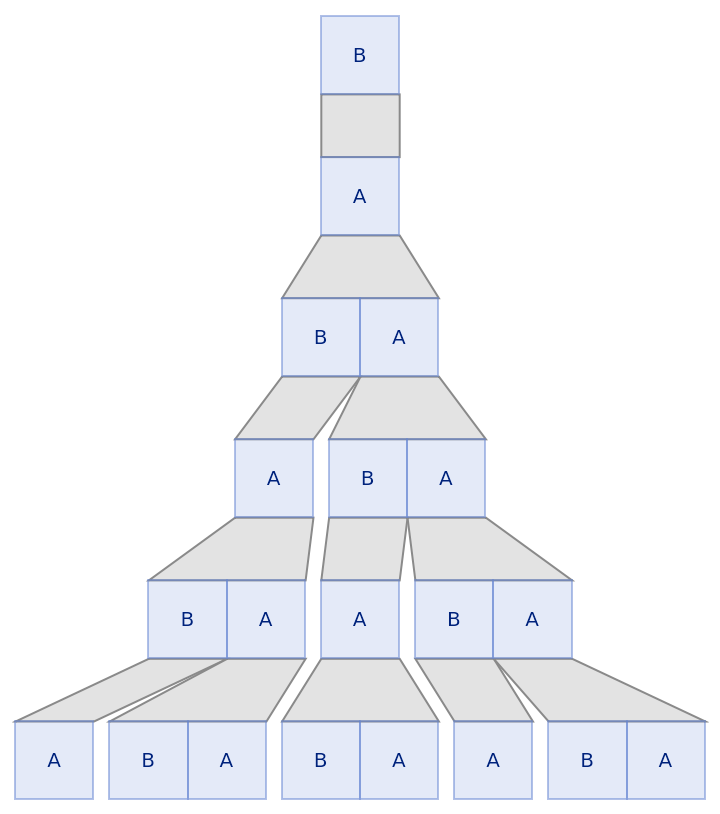 |
| In[10]:= |
| Out[10]= | 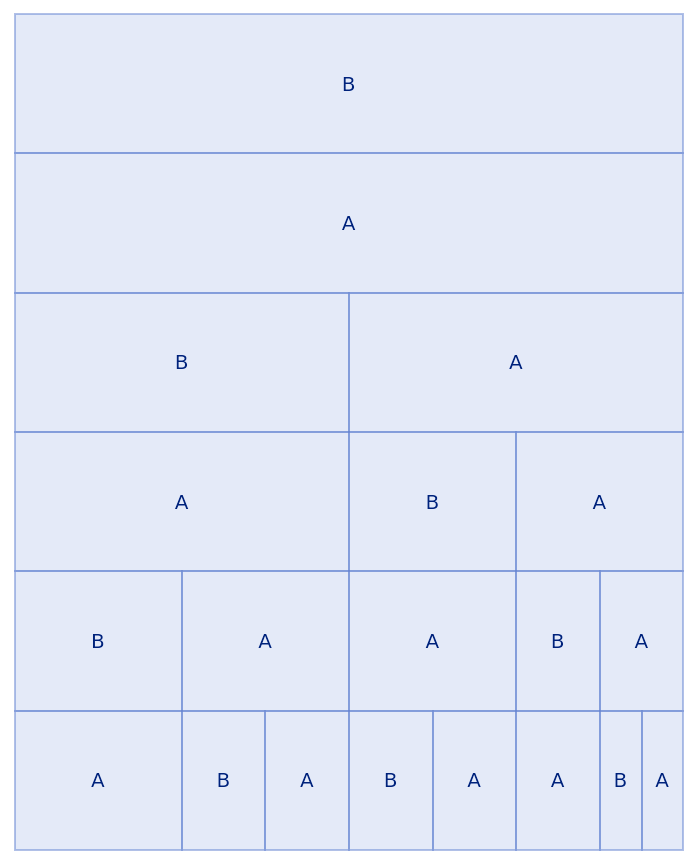 |
The initial condition can be of any length:
| In[11]:= |
| Out[11]= | 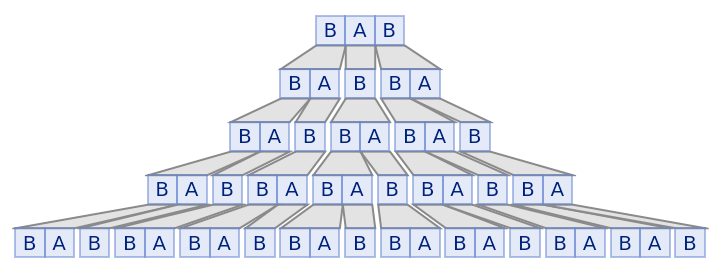 |
| In[12]:= |
| Out[12]= | 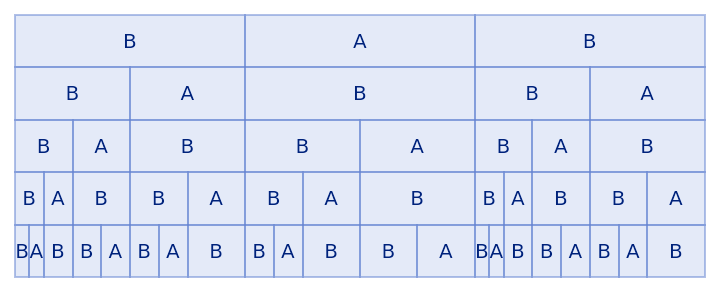 |
Rules can involve patterns:
| In[13]:= |
| Out[13]= | 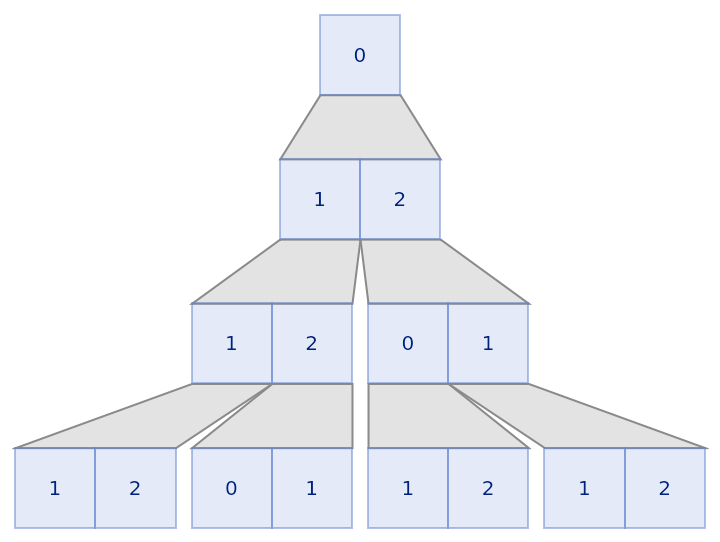 |
| In[14]:= |
| Out[14]= | 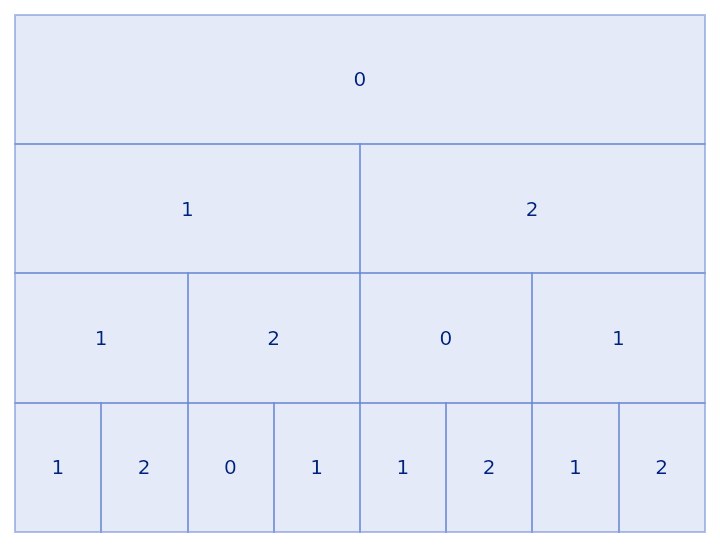 |
| In[15]:= |
| Out[15]= | 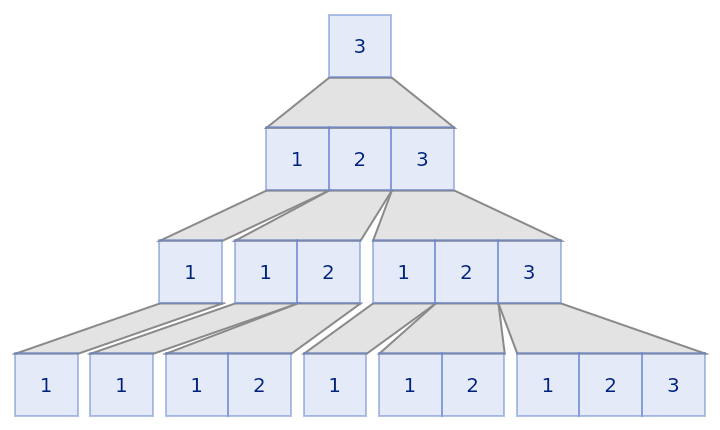 |
| In[16]:= |
| Out[16]= | 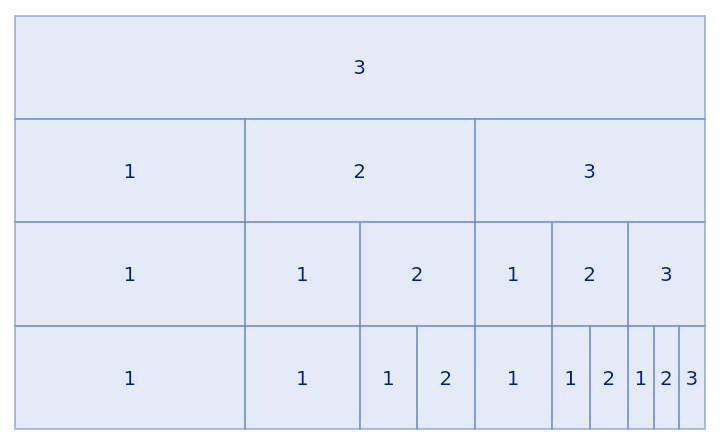 |
Use a string substitution system:
| In[17]:= |
| Out[17]= | 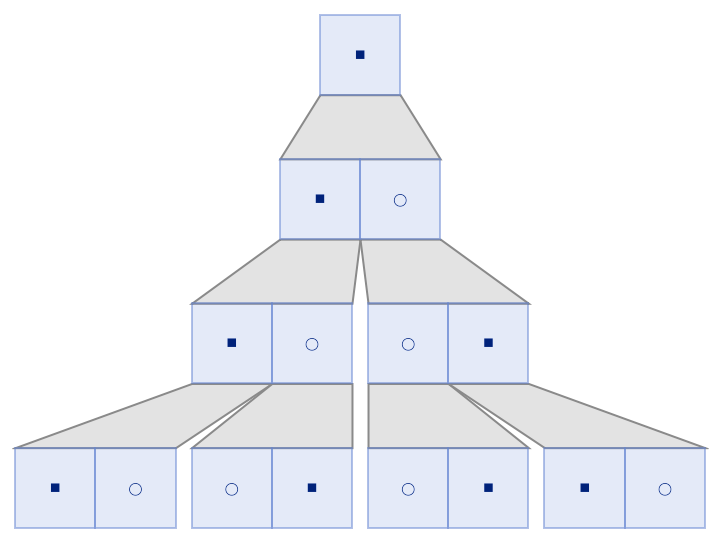 |
| In[18]:= |
| Out[18]= | 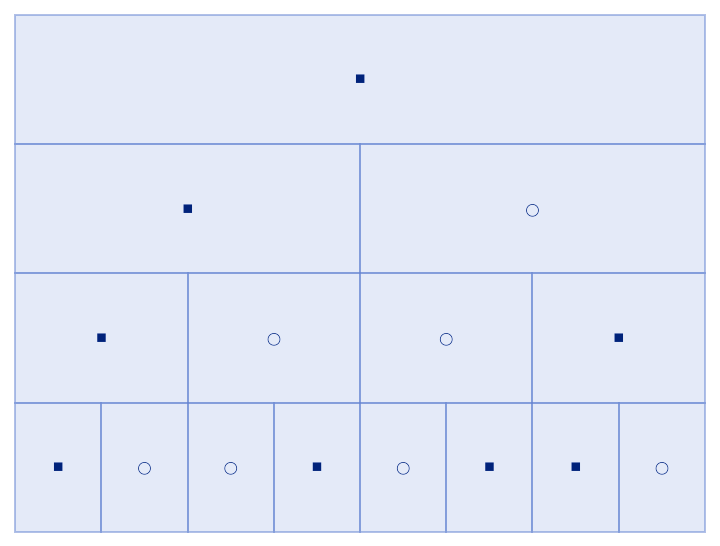 |
Different alignment formats for SubstitutionSystemPlot:
| In[19]:= |
| Out[19]= | 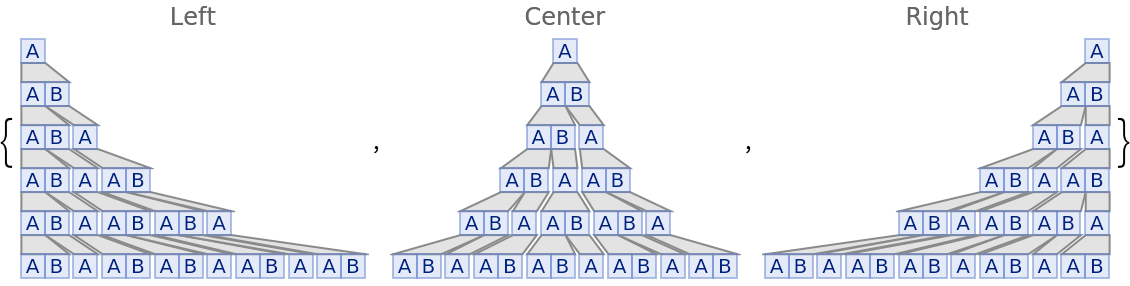 |
Show as boxes:
| In[20]:= |
| Out[20]= | 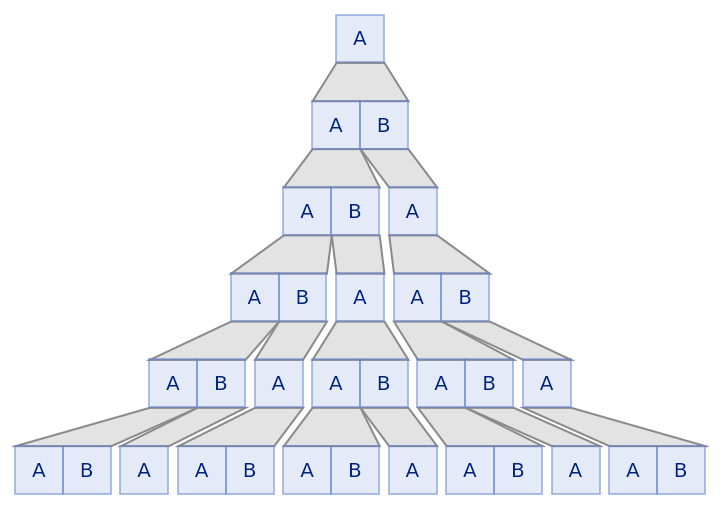 |
Show as an array:
| In[21]:= |
| Out[21]= | 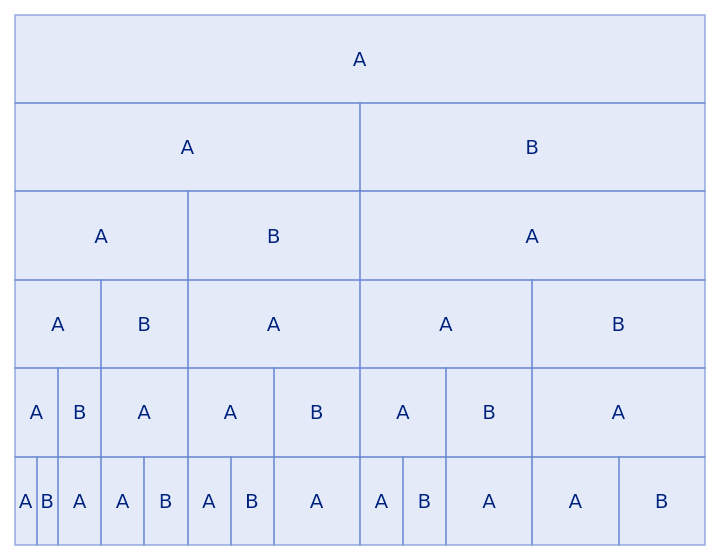 |
Show as a tree:
| In[22]:= |
| Out[22]= |  |
Specify color rules for explicit values or patterns:
| In[23]:= |
| Out[23]= | 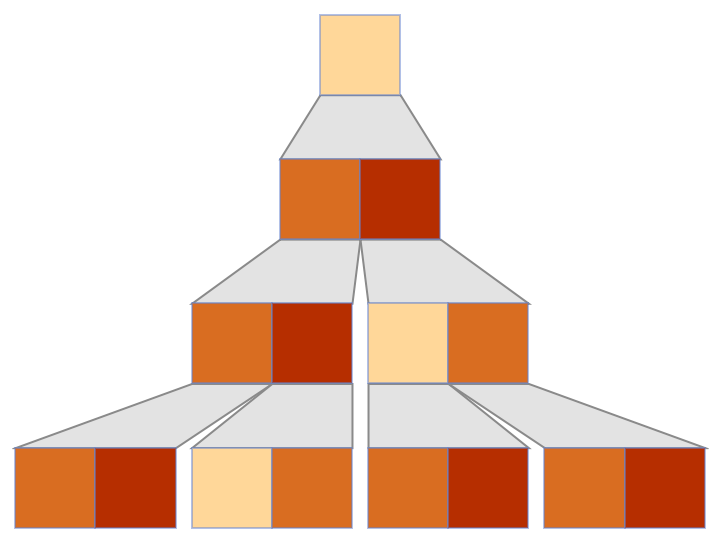 |
| In[24]:= |
| Out[24]= | 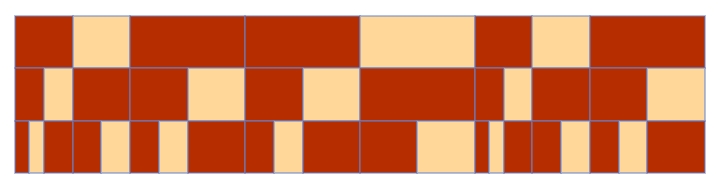 |
| In[25]:= |
| Out[25]= |  |
Implement a “default color” by adding a rule for _:
| In[26]:= |
| Out[26]= | 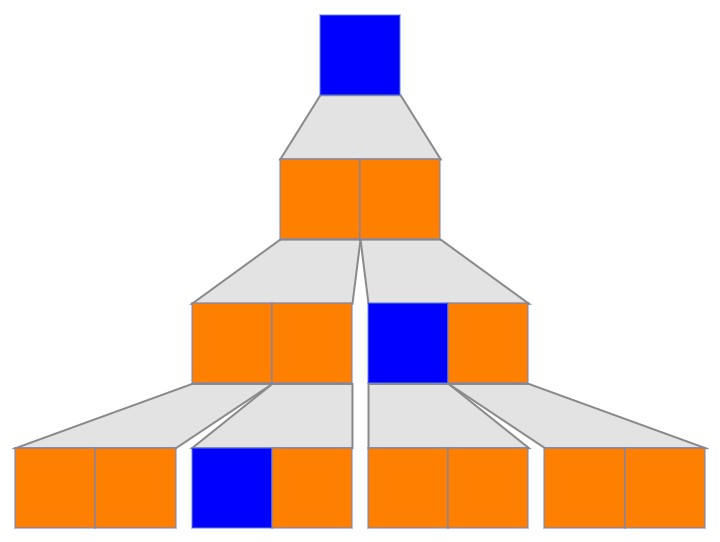 |
| In[27]:= |
| Out[27]= | 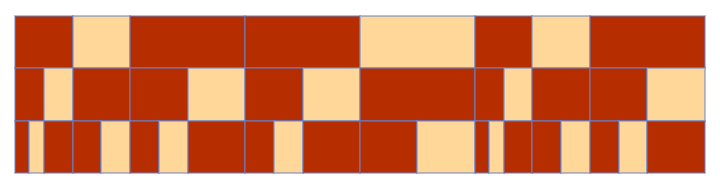 |
| In[28]:= |
| Out[28]= |  |
Show with and without the mesh:
| In[29]:= | ![GraphicsRow[
ResourceFunction[
"SubstitutionSystemPlot"][{"A" -> {"A", "B"}, "B" -> {"A"}}, {"A"}, 5, Mesh -> #] & /@ {True, False}]](https://www.wolframcloud.com/obj/resourcesystem/images/731/731ec6cd-912e-4d42-9803-d53fb99c741d/78e78f33145912b4.png) |
| Out[29]= | 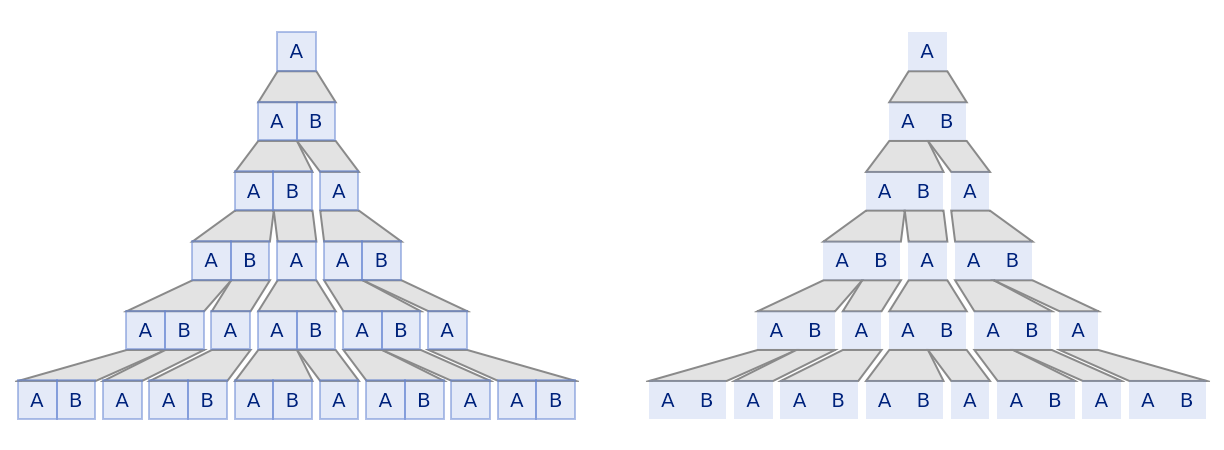 |
Make the mesh pink:
| In[30]:= |
| Out[30]= | 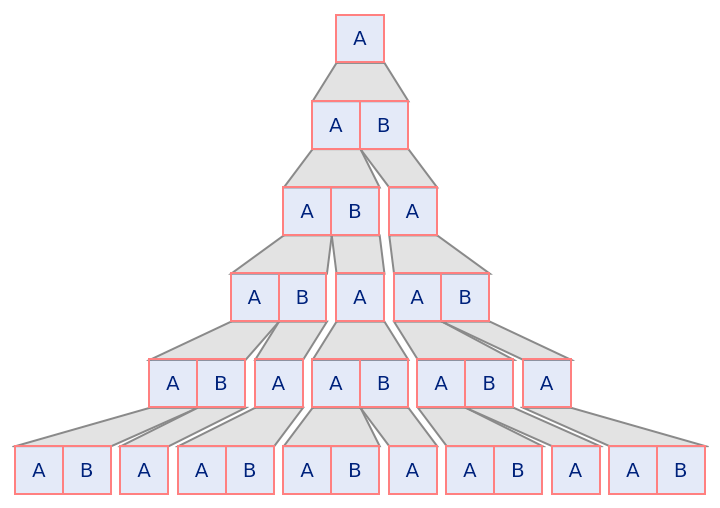 |
| In[31]:= |
| Out[31]= | 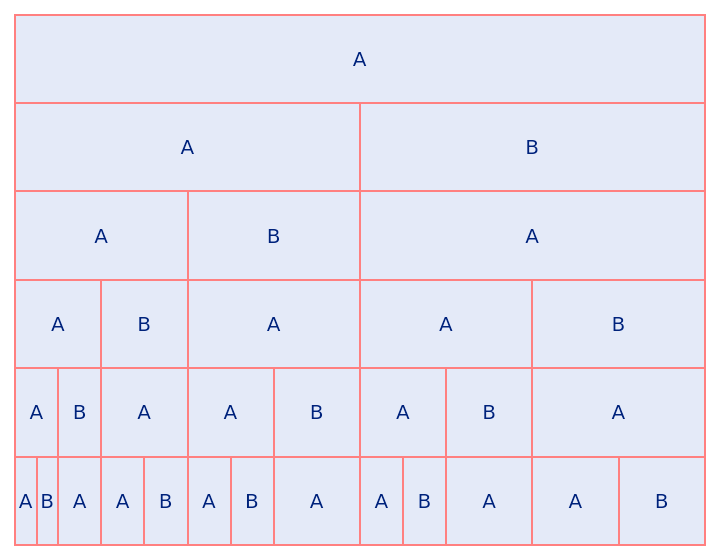 |
Different offsets for SubstitutionSystemPlot:
| In[32]:= | ![GraphicsRow[
ResourceFunction[
"SubstitutionSystemPlot"][{"A" -> {"A", "B"}, "B" -> {"A"}}, {"A"}, 5, Offset -> #] & /@ {1/10, 1/8, 1/2}]](https://www.wolframcloud.com/obj/resourcesystem/images/731/731ec6cd-912e-4d42-9803-d53fb99c741d/49d85d5624353a39.png) |
| Out[32]= | 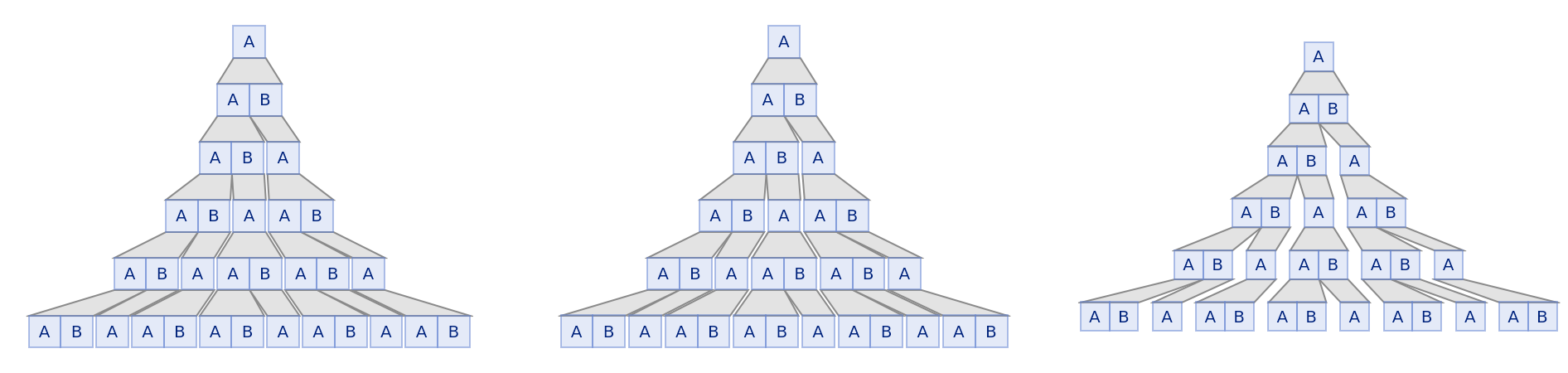 |
| In[33]:= | ![GraphicsRow[
ResourceFunction[
"SubstitutionSystemPlot"][{"A" -> {"A", "B"}, "B" -> {"A"}}, {"A"}, 5, Offset -> {1/5, #}] & /@ {6/5, 9/5, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/731/731ec6cd-912e-4d42-9803-d53fb99c741d/66c0ccb340efe335.png) |
| Out[33]= | 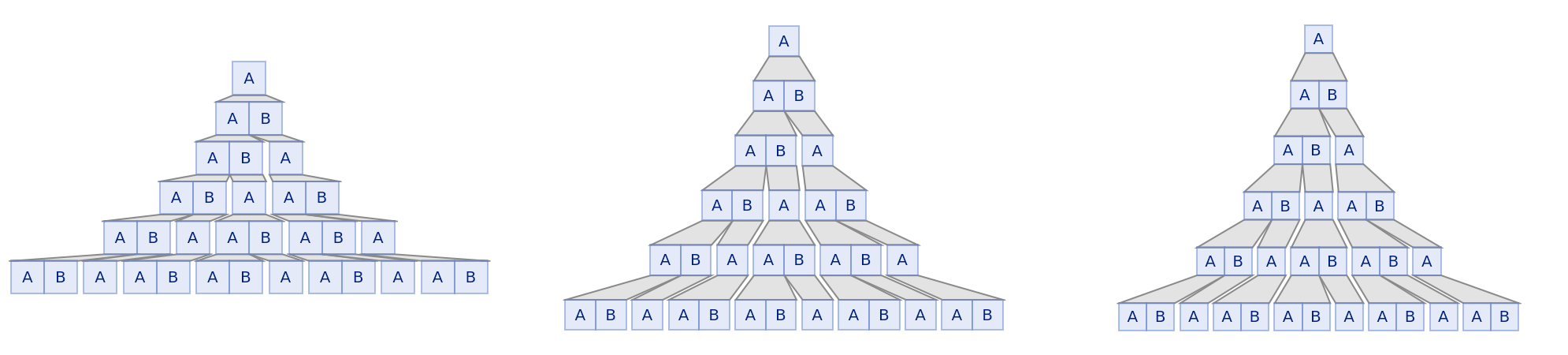 |
Illustrate the Thue-Morse substitution system:
| In[34]:= |
| Out[34]= | 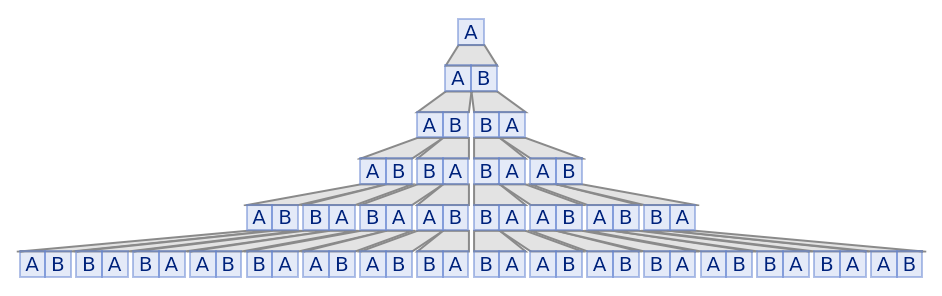 |
| In[35]:= |
| Out[35]= | 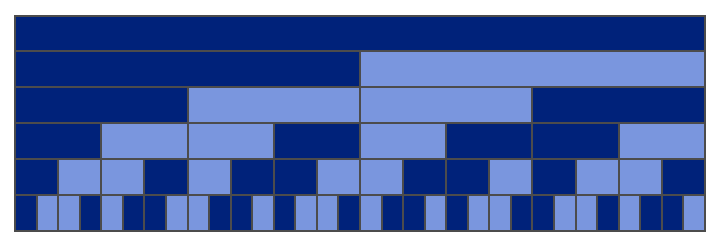 |
| In[36]:= |
| Out[36]= |  |
Illustrate the substitution system for the Cantor set:
| In[37]:= |
| Out[37]= | 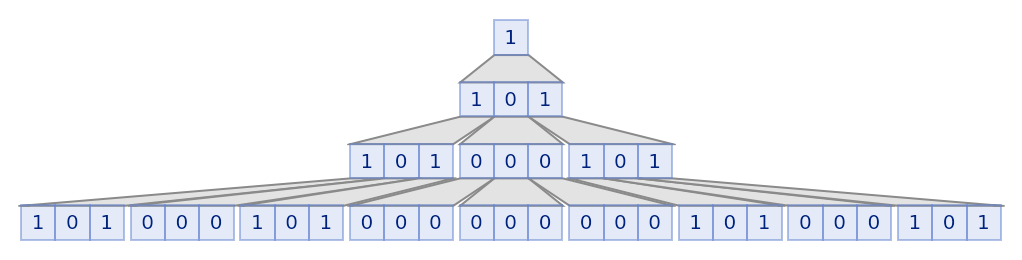 |
| In[38]:= |
| Out[38]= |  |
| In[39]:= |
| Out[39]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License