Details and Options
ResourceFunction["ActuarialCommutation"] functions can be used to compute a number of quantities of interest in actuarial mathematics, such as the value of an annuity or death benefit.
The parameter l is a list containing the fraction of the initial population surviving at the start of each time unit.
The parameter v is a discount rate generally between 0 and 1, showing the value of money received one year from now.
The "ReturnForm" option directs the form in which the data is returned: permissible option values are as follows:
"FunctionAssociation" returns an association in which the commutation function names are the keys and the values are the values of each function at each successive unit of time;
"TimeAssociation" returns a nested association in which the outer keys are the successive units of time and the values are associations in which the keys are the names of the commutation functions and the values are the value of that function at the specified unit of time.
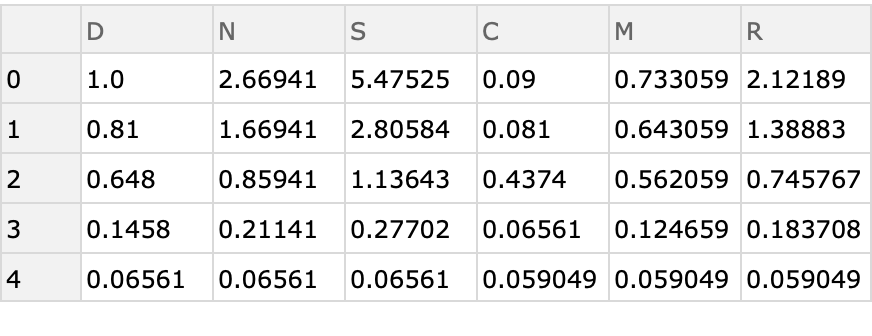
"FunctionValues" returns a nested list in which each outer list represents the values of a commutation function at a successive unit of time. The lists are ordered as "D", "N", "S", "C", "M", "R". For example, the fourth element of the returned values contains a list of the values for the "C" commutation function.
“TimeValues” returns a nested list in which each outer list represents a unit of time. Each inner list contains six values, one for each of the six commutation functions and in the order "D", "N", "S", "C", "M", "R".
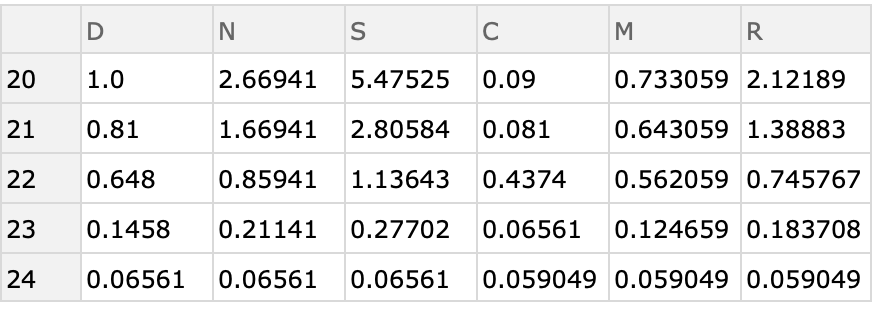
The "InitialTime" option can (and probably should) be used when the mortality table begins at an age other than 0.
Although commutation functions and tables displaying them are used less frequently than in times when computation was less accessible, they are still a useful tool in swiftly computing quanities of interest in actuarial mathematics.

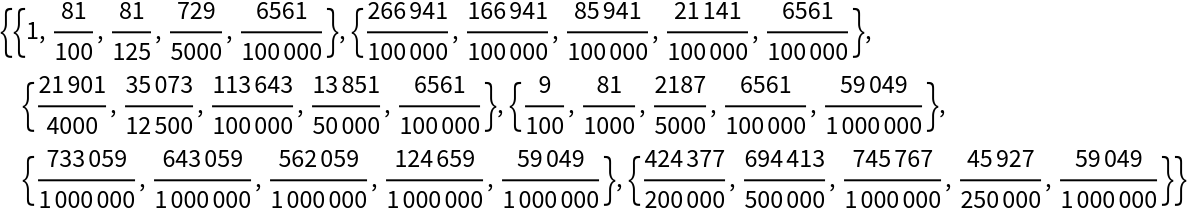
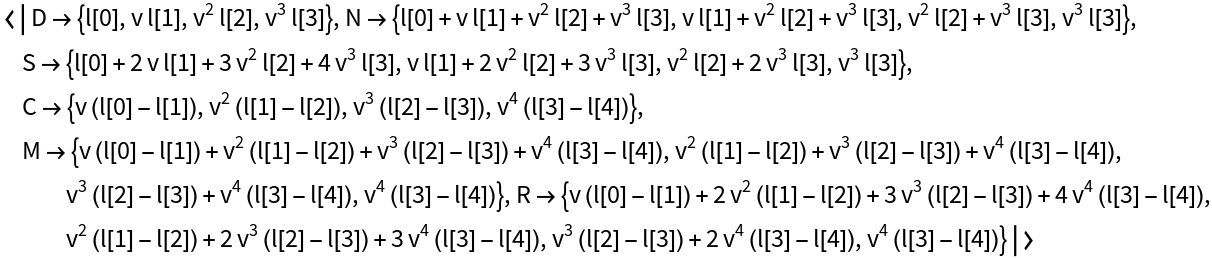
![ResourceFunction[
"ActuarialCommutation"][{1, 0.9846173379875812`, 0.9639606131621938`,
0.9325133217994516`, 0.8639769154117698`, 0.7361732007375918`, 0.5120752978556353`, 0.18294306933939167`, 0}, 0.95^10]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/52f53a1321d1be5c.png)

![Table[ResourceFunction[
"ActuarialCommutation"][{1, 0.9, 0.8, 0.2, 0.1, 0}, 0.9, "ReturnForm" -> form], {form, {"FunctionAssociation", "TimeAssociation", "FunctionValues", "TimeValues"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/363d3063ffbc762e.png)

![Table[ResourceFunction[
"ActuarialCommutation"][{1, 0.9, 0.8, 0.2, 0.1, 0}, 0.9, "ReturnForm" -> "TimeAssociation", "InitialTime" -> x], {x, {0, 20, 40}}]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/441e89a346521f4a.png)

![(maleMortality = 100000 ResourceFunction["MortalityConvert"][
ReplacePart[CompressedData["
1:eJw9UnssFAAc1jq5XNKDyKs5rc0rvTwW9cnRJJ07r8q5w53DPEPOqyONxJJ3
Wh4zCVlh4rTU6dwk5Cqi2OlQ8lrMvNsklfXHt+/3z/f4bZ8uO8yZu0VOTo6+
geOrfoWavS7IW9rmdc/RDXrG+U16Re6o5+jtqp2+iL0+4l5D7mUYU7SmR808
8CK2mhJ6k4GjElmyDcETrwihQ90uTPjmZD+tq2QipyvRvoXPxPybAzusllkQ
rbtvWHlju2YJS7/LG6q3HaYIJ3xAMxtTnI3wQaD6aXKFLfs/u4mqyqnWHBRJ
Z2kqExzMBXy91bjiC7+X6p1pPC4skg1M40u5OKU8IxkM8YepvvwQqycAXgqS
/fTBoM38EBS4U0Z1zoch4tchFfLwlU3/CDBbvM2DGVexOF9BVn3N2/wzGqT4
wZHajjhE8Y5ZOLD4m72v41KVabclNQn71Ouf90XegMaDKFfTM8mQ7qaSWAsp
mNzJ9lcsTsUSiScW2KWhrIBu1NSQju9dpLpMagaIj7U8fC0zUfWIG8TPzoL8
vwOZD5WZNFkOhIHcVpPFXHT5x+pIi/NRvCCca/S/C4VrCeq6Vvfha70Ut9xe
CO2OMZTLSuDoGqYUnF8KW3qp07dzZbCXciYpauX40UxekTlUIFnJqTaPW4UZ
YqW8yc9qtG3trPAceQLKOkHNMLAOKV5T4xfs6rF2xCamIbwB0k9JkWfzBJBp
fDYQjT5DFpW5avSuGcPzYuLIByHSearOCc4ijGtXTtgfFiN1RI/tcLANDGIE
rdWxHZROp2r+yU6sMzruZFi/RU1J7hdzoQSC+bWPMZPv4RjuNhBt1wN+jYCd
ONCLkEhOXOuePsj/mY12Pwh/hf34DZ6gLtg=
"], -1 -> 1], "Hazard" -> "Survival"]) // Short](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/3e57fd374b7c5252.png)
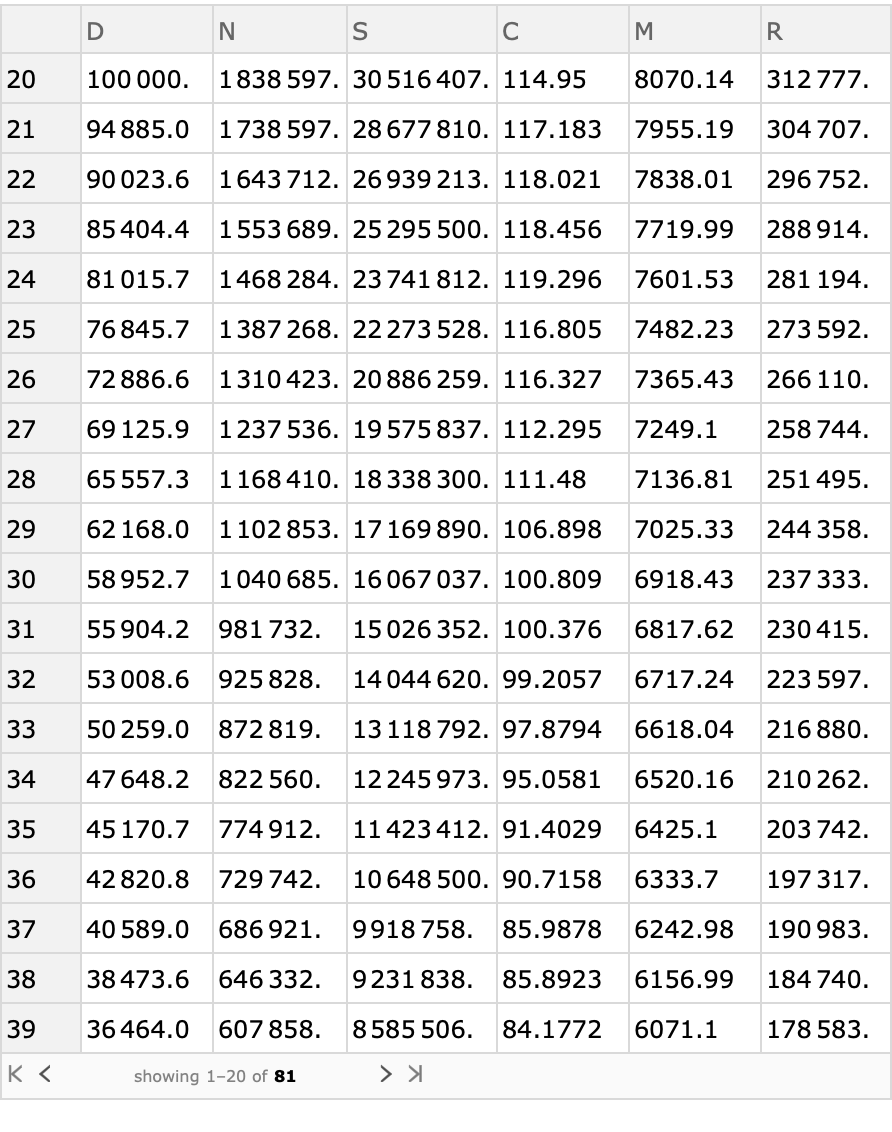
![males2017 = ResourceFunction["ActuarialCommutation"][maleMortality, 0.95, "ReturnForm" -> "TimeAssociation", "InitialTime" -> 20] // Dataset](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/1b64ee10fe3533bd.png)
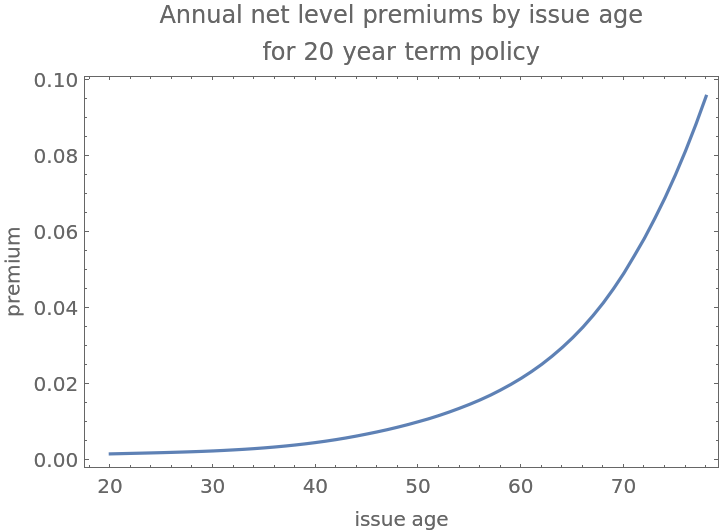
![With[{m = Normal@Query[All, #M &][males2017], n = Normal@Query[All, #N &][males2017]},
ListLinePlot[
Table[(m[[Key@x]] - m[[Key@(x + 20)]])/(
n[[Key@(x + 1)]] - n[[Key@(x + 20 + 1)]]), {x, 20, 78}], Sequence[
DataRange -> {20, 78}, Frame -> True, FrameLabel -> {"issue age", "premium"}, "PlotLabel" -> "Annual net level premiums by issue age\nfor 20 year term policy"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/087bcb61cab45026.png)
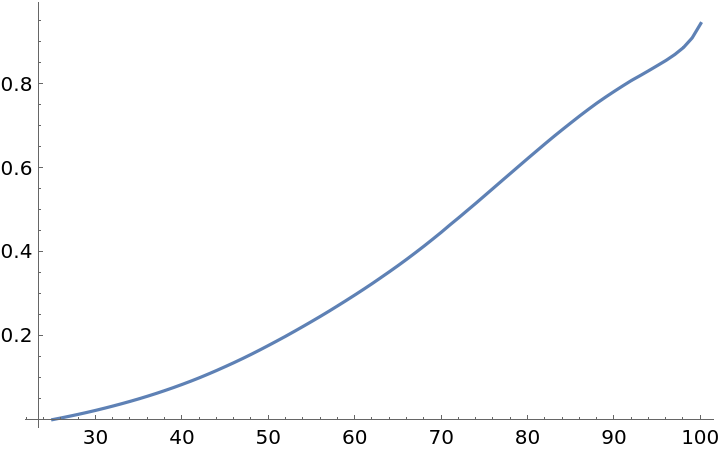
![retrospectiveReserve = Query[(Key /@ Range[25, 100])/*
ListLinePlot, (#M/#D - premiumMale25*#N/#D &)/*Chop][males2017]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/49912e89686b4033.png)
![1000000*((Query[Key@61, #M &][males2017] - Query[Key@(61 + 10), #M &][males2017])/
Query[Key@61, #D &][males2017])](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/48fce8875761e4fe.png)
![With[{\[ScriptCapitalM] = Normal[males2017[All, "M"]], \[ScriptCapitalD] = Normal[males2017[All, "D"]]}, 1000000 (\[ScriptCapitalM][61] - \[ScriptCapitalM][
61 + 10])/\[ScriptCapitalD][61]]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/6624f707161ab111.png)

![insuredMortality = 100000 ResourceFunction["MortalityConvert"][
ReplacePart[1.8*CompressedData["
1:eJw9UnssFAAc1jq5XNKDyKs5rc0rvTwW9cnRJJ07r8q5w53DPEPOqyONxJJ3
Wh4zCVlh4rTU6dwk5Cqi2OlQ8lrMvNsklfXHt+/3z/f4bZ8uO8yZu0VOTo6+
geOrfoWavS7IW9rmdc/RDXrG+U16Re6o5+jtqp2+iL0+4l5D7mUYU7SmR808
8CK2mhJ6k4GjElmyDcETrwihQ90uTPjmZD+tq2QipyvRvoXPxPybAzusllkQ
rbtvWHlju2YJS7/LG6q3HaYIJ3xAMxtTnI3wQaD6aXKFLfs/u4mqyqnWHBRJ
Z2kqExzMBXy91bjiC7+X6p1pPC4skg1M40u5OKU8IxkM8YepvvwQqycAXgqS
/fTBoM38EBS4U0Z1zoch4tchFfLwlU3/CDBbvM2DGVexOF9BVn3N2/wzGqT4
wZHajjhE8Y5ZOLD4m72v41KVabclNQn71Ouf90XegMaDKFfTM8mQ7qaSWAsp
mNzJ9lcsTsUSiScW2KWhrIBu1NSQju9dpLpMagaIj7U8fC0zUfWIG8TPzoL8
vwOZD5WZNFkOhIHcVpPFXHT5x+pIi/NRvCCca/S/C4VrCeq6Vvfha70Ut9xe
CO2OMZTLSuDoGqYUnF8KW3qp07dzZbCXciYpauX40UxekTlUIFnJqTaPW4UZ
YqW8yc9qtG3trPAceQLKOkHNMLAOKV5T4xfs6rF2xCamIbwB0k9JkWfzBJBp
fDYQjT5DFpW5avSuGcPzYuLIByHSearOCc4ijGtXTtgfFiN1RI/tcLANDGIE
rdWxHZROp2r+yU6sMzruZFi/RU1J7hdzoQSC+bWPMZPv4RjuNhBt1wN+jYCd
ONCLkEhOXOuePsj/mY12Pwh/hf34DZ6gLtg=
"], -1 -> 1], "Hazard" -> "Survival"]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/3aa4dd5b7b1dc19a.png)

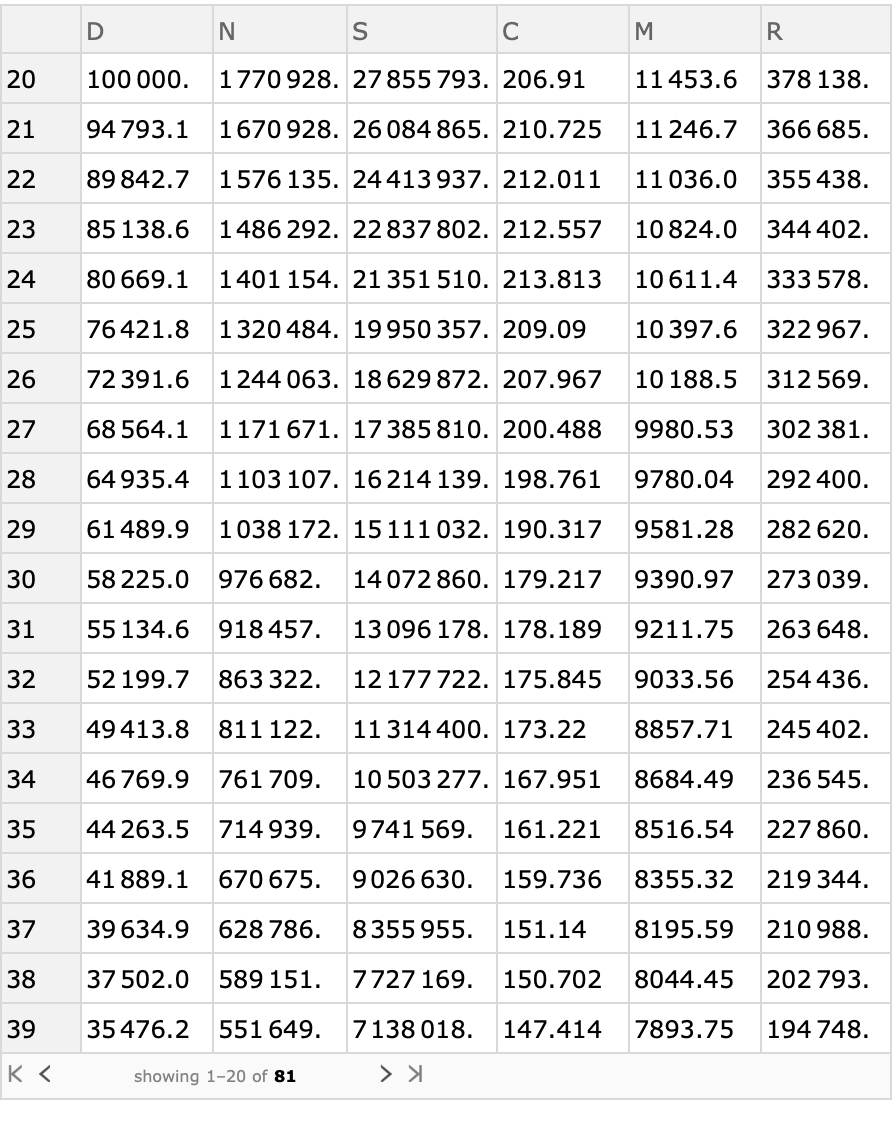
![insuredCommutation = ResourceFunction["ActuarialCommutation"][insuredMortality, 0.95, "ReturnForm" -> "TimeAssociation", "InitialTime" -> 20] // Dataset](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/2c6279d9d32f5348.png)
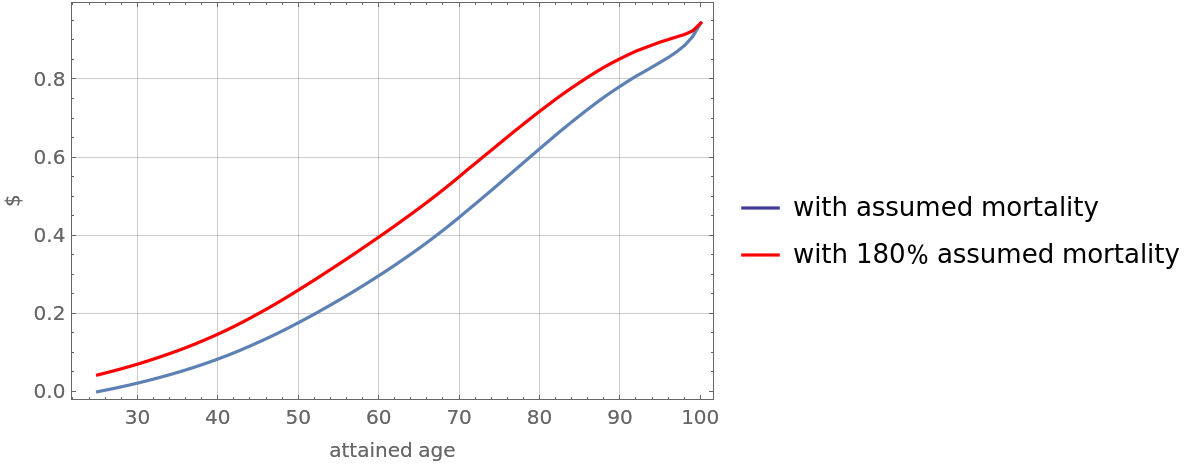
![Legended[
Show[retrospectiveReserve, Query[(Key /@ Range[25, 100])/*(ListLinePlot[#, PlotStyle -> Red] &), (#M/#D - premiumMale25*#N/#D &)/*Chop][
insuredCommutation], Sequence[
Frame -> True, FrameLabel -> {"attained age", "$"}, GridLines -> Automatic]], LineLegend[{
ColorData[1][1], Red}, {"with assumed mortality", "with 180% assumed mortality"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/72b/72b92312-7254-451c-a61f-6d1edb6e9fa7/1e77cd2efe0b1b60.png)