Basic Examples (4)
Convert a description of mortality using "Hazard" into an equivalent description using "Survival":
Convert the previous description of mortality using "Survival" into an equivalent description using "Probability":
Convert the previous description of mortality using "Probability" into an equivalent description using a cumulative distribution function (CDF):
Convert the previous description of mortality using a cumulative distribution function into an equivalent description using "Hazard" (returning, thereby, to the original input):
Scope (5)
If a symbolic vector is used as input, a conditional expression is generated:
The vector may be purely symbolic:
Conversions from one description to the same description return the original data:
If an impossible vector is used as input, the result is Undefined:
Unlisted representations (e.g. from spelling errors) generate a $Failed and an explanatory error message:
Applications (2)
Compute the expected value of death benefits with a mortality table given as a survival vector and a 100% interest rate, which is equivalent to a 50% discount rate:
Do the same computation using TimeValue and interest rates:
Compute the expected value of a premium of $1 paid at the beginning of each year the person is alive with a mortality table given as a hazard vector and a 100% interest rate:
Compute the premium required to set the expected value of premiums equal to the expected value of death benefits given mortality stated in different ways:
Neat Examples (2)
Compute the prospective reserve on an insurance policy at time z for which the insurer receives the same premium each year so long as the insured is alive, such that at the outset of the policy the expected time value of the premiums are equal to the expected time value of the death benefits:
An insurer pays 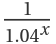 if risk 1 first materializes at time x and pays
if risk 1 first materializes at time x and pays 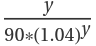 if risk 2 first materializes at time y, where the materialization of the risks are independent and the distribution of time at which either materializes is given as a list of hazard probabilities. Compute the expected present value of the insurer’s payout, assuming a 5% interest rate:
if risk 2 first materializes at time y, where the materialization of the risks are independent and the distribution of time at which either materializes is given as a list of hazard probabilities. Compute the expected present value of the insurer’s payout, assuming a 5% interest rate:

![Expectation[0.5^t, t \[Distributed] EmpiricalDistribution[
ResourceFunction["MortalityConvert"][{1, 0.8, 0.48, 0}, "Survival" -> "Probability"] -> {1, 2, 3}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/4ad698836213a830.png)
![Expectation[TimeValue[Cashflow[{{t, 1}}], 1, 0], t \[Distributed] EmpiricalDistribution[
ResourceFunction["MortalityConvert"][{0.2, 0.4, 1}, "Hazard" -> "Probability"] -> {1, 2, 3}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/7cfcede5d534330d.png)
![Expectation[TimeValue[AnnuityDue[1, t], 1, 0], t \[Distributed] EmpiricalDistribution[
ResourceFunction["MortalityConvert"][{0.2, 0.4, 1}, "Hazard" -> "Probability"] -> {1, 2, 3}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/5289a27c9c44c82e.png)
![With[{dist = EmpiricalDistribution[
ResourceFunction["MortalityConvert"][{1, 0.8, 0.48, 0}, "Survival" -> "Probability"] -> {1, 2, 3}]}, Solve[Expectation[0.5^t, t \[Distributed] dist] == Expectation[TimeValue[AnnuityDue[p, payments], 1, 0], payments \[Distributed] dist], p]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/64f29c3e7c87fd59.png)
![prospectiveReserve[dist_, z_] := Module[{timeShiftedDist, premium},
timeShiftedDist = timeShiftedDistribution[z, dist];
premium = p /. First@
Solve[Expectation[TimeValue[Cashflow[{{t, 1}}], 1, 0], t \[Distributed] dist] == Expectation[TimeValue[AnnuityDue[p, payments], 1, 0], payments \[Distributed] dist], p];
Expectation[TimeValue[Cashflow[{{t, 1}}], 1, 0], t \[Distributed] timeShiftedDist] - Expectation[TimeValue[AnnuityDue[premium, payments], 1, 0], payments \[Distributed] timeShiftedDist]
]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/38b805eb196a876c.png)
![Table[{z, prospectiveReserve[
EmpiricalDistribution[
ResourceFunction["MortalityConvert"][{1, 0.8, 0.48, 0}, "Survival" -> "Probability"] -> {1, 2, 3}], z]}, {z, 0, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/5c2d24c55d3073ed.png)
![]() if risk 1 first materializes at time x and pays
if risk 1 first materializes at time x and pays ![]() if risk 2 first materializes at time y, where the materialization of the risks are independent and the distribution of time at which either materializes is given as a list of hazard probabilities. Compute the expected present value of the insurer’s payout, assuming a 5% interest rate:
if risk 2 first materializes at time y, where the materialization of the risks are independent and the distribution of time at which either materializes is given as a list of hazard probabilities. Compute the expected present value of the insurer’s payout, assuming a 5% interest rate:![probability1 = EmpiricalDistribution[
ResourceFunction["MortalityConvert"][(90^6 - Range[0, 90]^6)/90^6, "Survival" -> "Probability"] -> Range[0, 89]]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/3b22ab0d26b471e5.png)
![NExpectation[
If[x < y, TimeValue[Cashflow[{{x, 1/1.04^x}}], 0.05, 0], TimeValue[Cashflow[{{y, y/(90 (1.04)^y)}}], 0.05, 0]], {x, y} \[Distributed] ProductDistribution[probability1, probability2]]](https://www.wolframcloud.com/obj/resourcesystem/images/d6a/d6a8caca-d1fc-4ed8-95d8-053c0bd6fc6a/2b2aae2cfdecb158.png)