Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ConfusionMatrixFlip

Source Notebook

Alter a confusion matrix by stochastically flipping classification results

Contributed by: Seth J. Chandler

ResourceFunction["ConfusionMatrixFlip"][m,r]

flips a matrix m using a matrix r in which rij represents the fraction of instances for which an instance in column i will flip into column j.

ResourceFunction["ConfusionMatrixFlip"][m,flips]

flips a 2×2 matrix using a vector to give the proportions of flips between columns.

Details and Options

In typical usage, m will be a confusion matrix.
Entries in the confusion matrix or flip must be non-negative.
Since they represent probabilities, rows of the flip matrix must total to 1.

Examples

Basic Examples (2) 

Flip a 2×2 confusion matrix by randomly reversing 20% of the instances classified as negative and 40% of the instances classified as positive:

In[1]:=
ResourceFunction[ "ConfusionMatrixFlip"][{{40, 30}, {10, 20}}, {{0.8, 0.2}, {0.4, 0.6}}]
Out[1]=

Use a simplified syntax to accomplish the same flip :

In[2]:=
ResourceFunction[ "ConfusionMatrixFlip"][{{40, 30}, {10, 20}}, {0.2, 0.4}]
Out[2]=

Flip a 3 ×3 matrix by moving 30% of those classified as 1 to 2 and 10% of those classified as 1 to 3; by moving 0% of those classified as 2 to 1 and 40% of those classified as 2 to 3; and by moving 50% of those classified as 3 to 2 and 10% of those classified as 3 to 1:

In[3]:=
ResourceFunction[ "ConfusionMatrixFlip"][{{20, 40, 10}, {5, 10, 5}, {8, 1, 1}}, {{0.6, 0.3, 0.1}, {0, 0.6, 0.4}, {0.1, 0.5, 0.4}}]
Out[3]=

Scope (1) 

Both the confusion matrix and the flip matrix can be symbolic:

In[4]:=
ResourceFunction["ConfusionMatrixFlip"][ Array[Subscript[cm, ##] &, {3, 3}], Map[#/Total[#] &, Array[Subscript[flip, ##] &, {3, 3}]]]
Out[4]=

Applications (3) 

Find out how much the accuracy of a classifier declines using a symbolic confusion matrix and symbolic set of flips:

In[5]:=
Collect[Simplify@ Module[{m = Array[Subscript[cm, ##] &, {2, 2}], originalAccuracy, flippedAccuracy}, originalAccuracy = Total@Diagonal[m]/Total[m, 2]; flippedAccuracy = 1/Total[m, 2] Total@ Diagonal[ ResourceFunction["ConfusionMatrixFlip"][m, {flipneg, flippos}]]; 1 - flippedAccuracy/originalAccuracy], {flipneg, flippos}]
Out[5]=

Given an original 2×2 confusion matrix, find the set of flips such that the false positive rate and true positive rate equal some pair {fpr,tpr}:

In[6]:=
With[{flipped = ResourceFunction["ConfusionMatrixFlip"][ Array[Subscript[cm, ##] &, {2, 2}], {flipneg, flippos}]}, Solve[{flipped[[1, 2]]/Total[flipped[[1]]] == fpr, flipped[[2, 2]]/Total[flipped[[2]]] == tpr}, {flipneg, flippos}]] // FullSimplify
Out[6]=

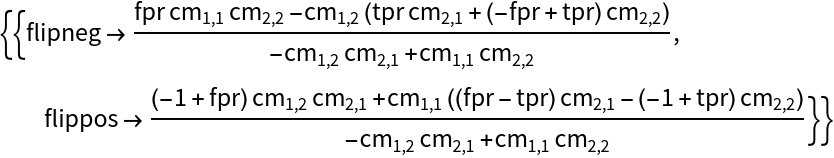
Given an original 2×2 confusion matrix, find the set of flips such that the positive classification rate equals some value pcr:

In[7]:=
With[{flipped = ResourceFunction["ConfusionMatrixFlip"][ Array[Subscript[cm, ##] &, {2, 2}], {flipneg, flippos}]}, Quiet[Solve[{(flipped[[1, 2]] + flipped[[2, 2]])/ Total[flipped, 2] == pcr}, {flipneg, flippos}]]] // FullSimplify
Out[7]=

Neat Examples (2) 

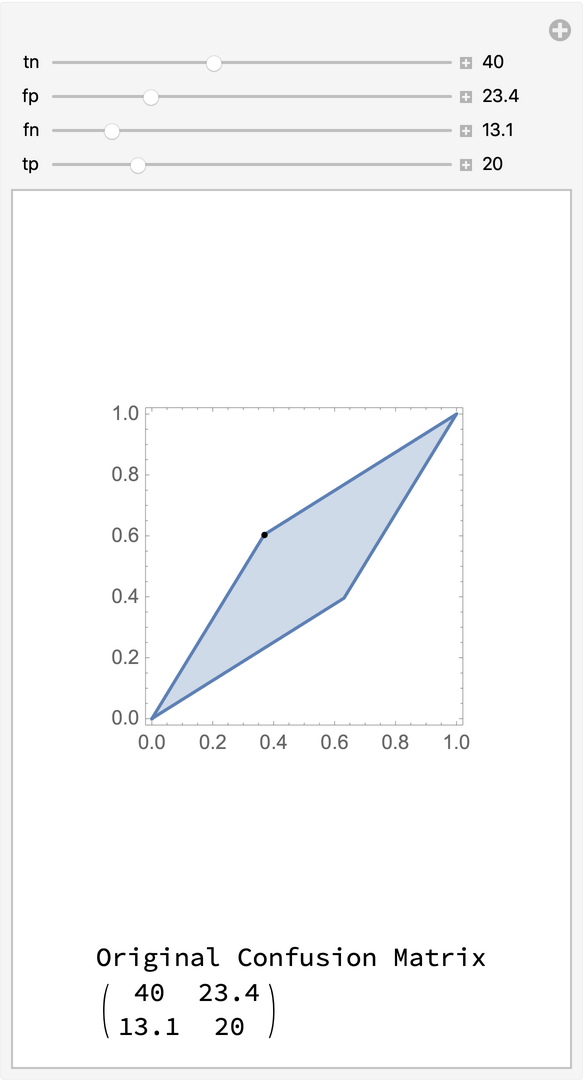
Show the set of possible false positive rates and true positive rates attainable by flipping a confusion matrix derived from a classifier:

In[8]:=
Manipulate[Module[{cm = {{tn, fp}, {fn, tp}}, flipped, fpr, tpr}, Labeled[ RegionPlot[ 0 <= (fpr (cm[[1, 1]] + cm[[1, 2]]) cm[[2, 2]] - tpr cm[[1, 2]] (cm[[2, 1]] + cm[[2, 2]]))/(-cm[[1, 2]] cm[[2, 1]] + cm[[1, 1]] cm[[2, 2]]) <= 1 && 0 <= ((tpr cm[[1, 1]] + cm[[1, 2]] - fpr (cm[[1, 1]] + cm[[1, 2]])) cm[[2, 1]] + (-1 + tpr) cm[[1, 1]] cm[[2, 2]])/(cm[[1, 2]] cm[[2, 1]] - cm[[1, 1]] cm[[2, 2]]) <= 1, {fpr, 0, 1}, {tpr, 0, 1}, Epilog -> {PointSize[0.02], Point[{fp/(fp + tn), tp/(tp + fn)}]}], Column[{"Original Confusion Matrix", MatrixForm[{{tn, fp}, {fn, tp}}]}]] ], {{tn, 40}, 0.1, 100, Appearance -> "Labeled"}, {{fp, 30}, 0.1, 100, Appearance -> "Labeled"}, {{fn, 10}, 0.1, 100, Appearance -> "Labeled"}, {{tp, 20}, 0.1, 100, Appearance -> "Labeled"}]
Out[8]=

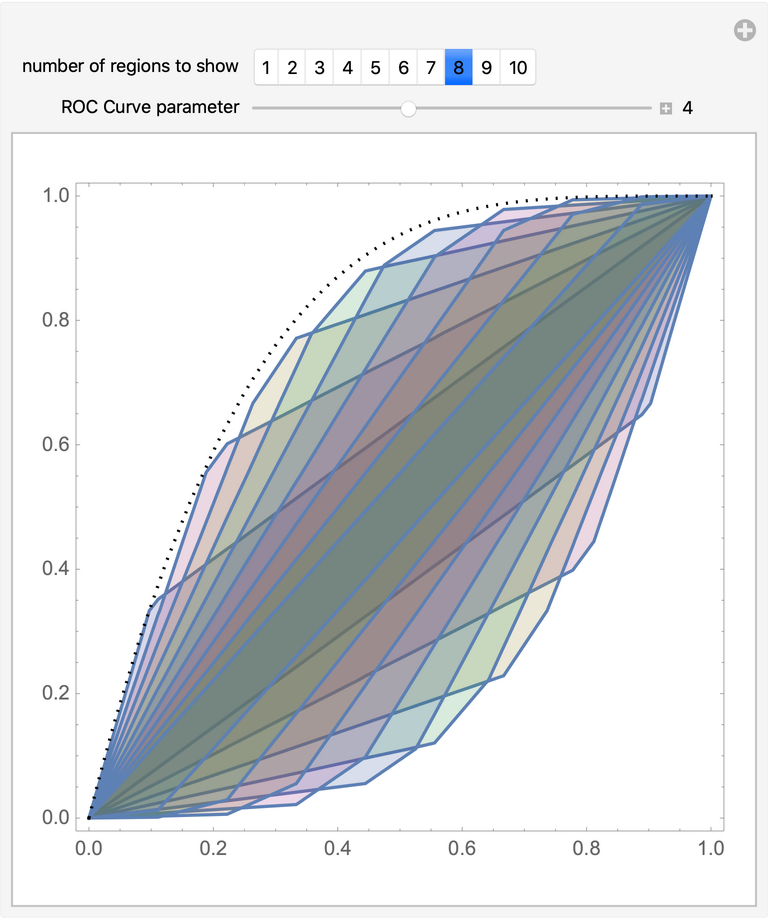
Approximate the region of attainable false positive and true positive rates given a receiver operating characteristic curve (shown as a dotted line) and a set of flips:

In[9]:=
Manipulate[ Show @@ Append[ MapIndexed[{f, index} |-> With[{att = attainable[f, CDF[BetaDistribution[1, rocvalue]], 0.5]}, RegionPlot[att[fpr, tpr], {fpr, 0, 1}, {tpr, 0, 1}, PlotStyle -> {Opacity[0.2], ColorData[1][index[[1]]]}] ], Subdivide[0.1, 0.9, n]], Plot[CDF[BetaDistribution[1, rocvalue], f], {f, 0, 1}, PlotStyle -> Directive[{Dotted, Black}]]], {{n, 8, "number of regions to show"}, Range[10], ControlType -> SetterBar}, {{rocvalue, 4, "ROC Curve parameter"}, 1.5, 8, 0.1, Appearance -> "Labeled"}, Initialization :> (attainable[cm_] = Function[{fpr, tpr}, 0 <= (fpr (cm[[1, 1]] + cm[[1, 2]]) cm[[2, 2]] - tpr cm[[1, 2]] (cm[[2, 1]] + cm[[2, 2]]))/(-cm[[1, 2]] cm[[ 2, 1]] + cm[[1, 1]] cm[[2, 2]]) <= 1 && 0 <= ((tpr cm[[1, 1]] + cm[[1, 2]] - fpr (cm[[1, 1]] + cm[[1, 2]])) cm[[2, 1]] + (-1 + tpr) cm[[1, 1]] cm[[2, 2]])/(cm[[1, 2]] cm[[2, 1]] - cm[[1, 1]] cm[[2, 2]]) <= 1]; attainable[fpr_, tprfunc_, i_] := attainable[{{1 - fpr - i + fpr i, fpr - fpr i}, {i - i tprfunc[fpr], i tprfunc[fpr]}}])]
Out[9]=

Publisher

Seth J. Chandler

Version History

  • 1.0.0 – 23 October 2020

Related Resources

License Information