Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CongruentIncirclePartition

Source Notebook

Find the partition of a triangle into cevian triangles with congruent incircles

Contributed by: Shenghui Yang and Xianwen Wang

ResourceFunction["CongruentIncirclePartition"][{p1,p2,p3},n]

partition a triangle defined by vertices p1,p2 and p3 into cevian triangles that share vertex p1 and the same inradius.

Details

CongruentIncirclePartition returns an Association containing the following items:
"Partitions"The number n of cevian triangles
"Inradius"The radius of the incircle in each cevian triangle
"Incircles"The congruent incircles
"CevianEndpoints"The vertices of each cevian triangle other than p1 on segment p2p3
"CevianTriangles"Cevian triangles from by p1and two adjacent in "CevianEndpoints"
ResourceFunction["CongruentIncirclePartition"][Triangle[vert],n] is equivalent to ResourceFunction["CongruentIncirclePartition"][vert,n]

Examples

Basic Examples (1) 

Return an association containing the information of a partition of a given triangle into subtriangles sharing incircles of same size:

In[1]:=
v = {{0.974, 1.4}, {0.4, 0.46}, {1.6, 0.54}}; res = ResourceFunction["CongruentIncirclePartition"][v, 3]
Out[2]=

Scope (3) 

Find a cevian partition of a given triangle into 7 triangle with incircles of same size:

In[3]:=
v = {{1.3, 1.2}, {0.4, 0.46}, {1.6, 0.54}};
In[4]:=
label[sym_, Point[pos_]] := {PointSize[Scaled[0.063]], RGBColor["#000814"], Point[pos], Text[Style[sym, White, FontSize -> Scaled[0.035]], pos]};
In[5]:=
res = ResourceFunction["CongruentIncirclePartition"][v, 7]; Graphics[{ {Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], res["CevianTriangles"]}, {Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[v]}, {Thick, RGBColor["#003566"], res["Incircles"]}, MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ v}] }, ImageSize -> 400]
Out[6]=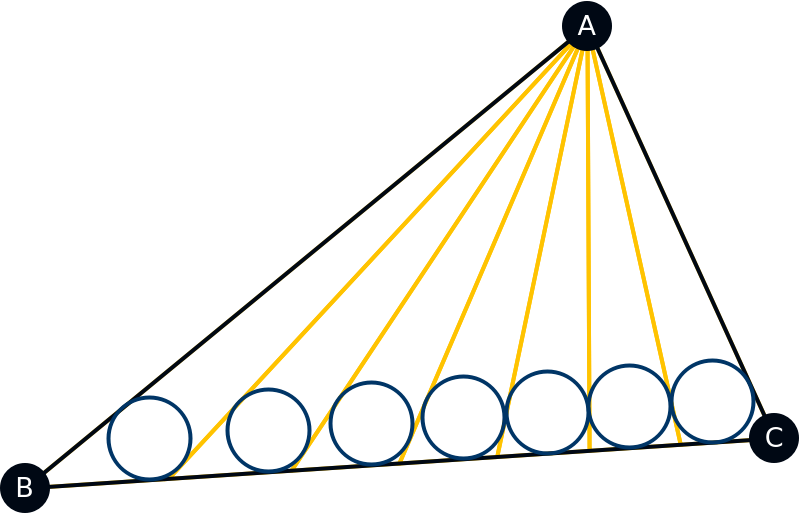

For each orientation, find a 4-part cevian partition:

In[7]:=
v = {{1.3, 1.2}, {0.4, 0.46}, {1.6, 0.54}}; rv = RotateRight[v, #] & /@ {0, 1, 2};
In[8]:=
label[sym_, Point[pos_]] := {PointSize[Scaled[0.066]], RGBColor["#000814"], Point[pos], Text[Style[sym, White, FontSize -> Scaled[0.04]], pos]};
In[9]:=
GraphicsRow[Table[ res = ResourceFunction["CongruentIncirclePartition"][ele, 4]; Graphics[{ {Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], res["CevianTriangles"]}, {Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[v]}, {Thick, RGBColor["#003566"], res["Incircles"]}, MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ v}] }], {ele, rv}], ImageSize -> 870, Dividers -> All, ImagePadding -> 4]
Out[9]=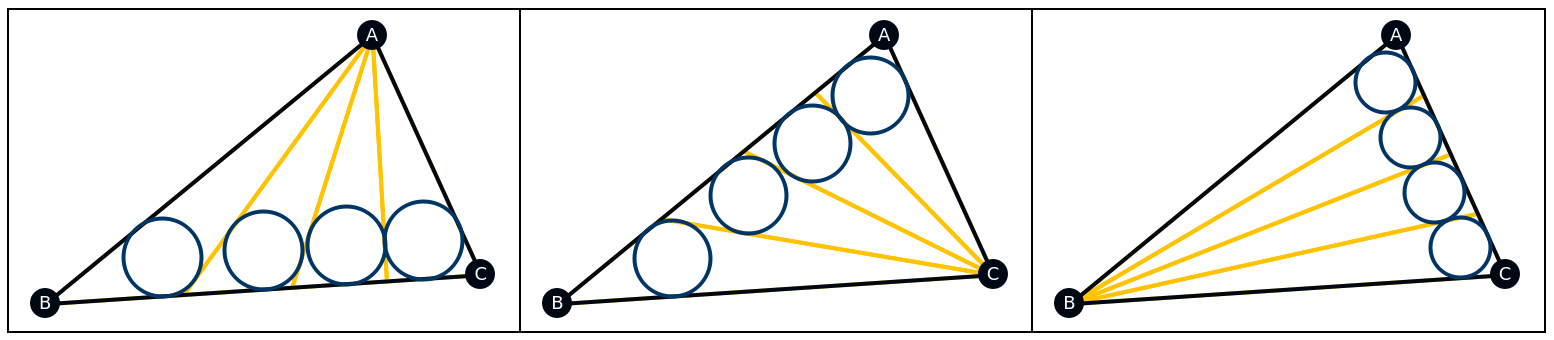

Certain triangles with integral sides also have integral inradii in a cevian triangle partition:

In[10]:=
res = ResourceFunction["CongruentIncirclePartition"][ SSSTriangle[75, 65, 20], 4];
In[11]:=
res["Inradius"]
Out[11]=
In[12]:=
res = ResourceFunction["CongruentIncirclePartition"][ SSSTriangle[27744, 11475, 24531], 4];
In[13]:=
res["Inradius"]
Out[13]=

Possible Issues (3) 

The number of partition must be at least 2. Otherwise the function returns unevaluated:

In[14]:=
ResourceFunction[ "CongruentIncirclePartition"][{{1.3, 1.2}, {0.4, 0.46}, {1.6, 0.54}}, 1]
Out[14]=
In[15]:=
ResourceFunction[ "CongruentIncirclePartition"][{{1.3, 1.2}, {0.4, 0.46}, {1.6, 0.54}}, 2]
Out[15]=

Degenerate triangles are not supported. The function returns unevaluated:

In[16]:=
ResourceFunction["CongruentIncirclePartition"][{{1, 1}, {2, 2}, {3, 3}}, 6]
Out[16]=

Perturb one vertex to create a non-degenerate case:

In[17]:=
ResourceFunction[ "CongruentIncirclePartition"][{{1, 1}, {2, 2.01}, {3, 3}}, 3]
Out[17]=

Coordinates must be real numeric values. Otherwise the function returns unevaluated:

In[18]:=
ResourceFunction["CongruentIncirclePartition"][{{1, y}, {2, x}, {3, 3}}, 3]
Out[18]=

Neat Examples (6) 

Given an arbitrary triangle, let n-1 cevians be drawn from one of its vertices so all of the n triangles so determined have equal incircles. Then the incircles determined by spanning 2, 3,…, n-1 adjacent triangles are also equal (Wells 1991, p. 67). For instance, a spanning set of size 2:

In[19]:=
vert = {{1.3, 1.2}, {0.4, 0.46}, {1.6, 0.54}}; eps = {vert[[2]]}~Join~ ResourceFunction["CongruentIncirclePartition"][vert, 7][ "CevianEndpoints"]~Join~{vert[[3]]};

Check the inradii:

In[20]:=
gapTri = Triangle[{vert[[1]], #1, #2}] & @@@ Table[eps[[{k, k + 2}]], {k, 1, 6}]; TriangleMeasurement[#, "Inradius"] & /@ gapTri
Out[21]=

Visualize the cevian triangles and the incircles:

In[22]:=
label[sym_, Point[pos_]] := {PointSize[Scaled[0.066]], RGBColor["#000814"], Point[pos], Text[Style[sym, White, FontSize -> Scaled[0.04]], pos]};
In[23]:=
GraphicsGrid[Partition[#, 3] &@Table[ Graphics[{ {LightGray, Line[{vert[[1]], #}] & /@ eps}, {Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], tri}, {Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[vert]}, {Thick, RGBColor["#003566"], TriangleConstruct[tri, "Incircle"]}, MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ vert}] }], {tri, gapTri}], ImageSize -> 780, Dividers -> All]
Out[23]=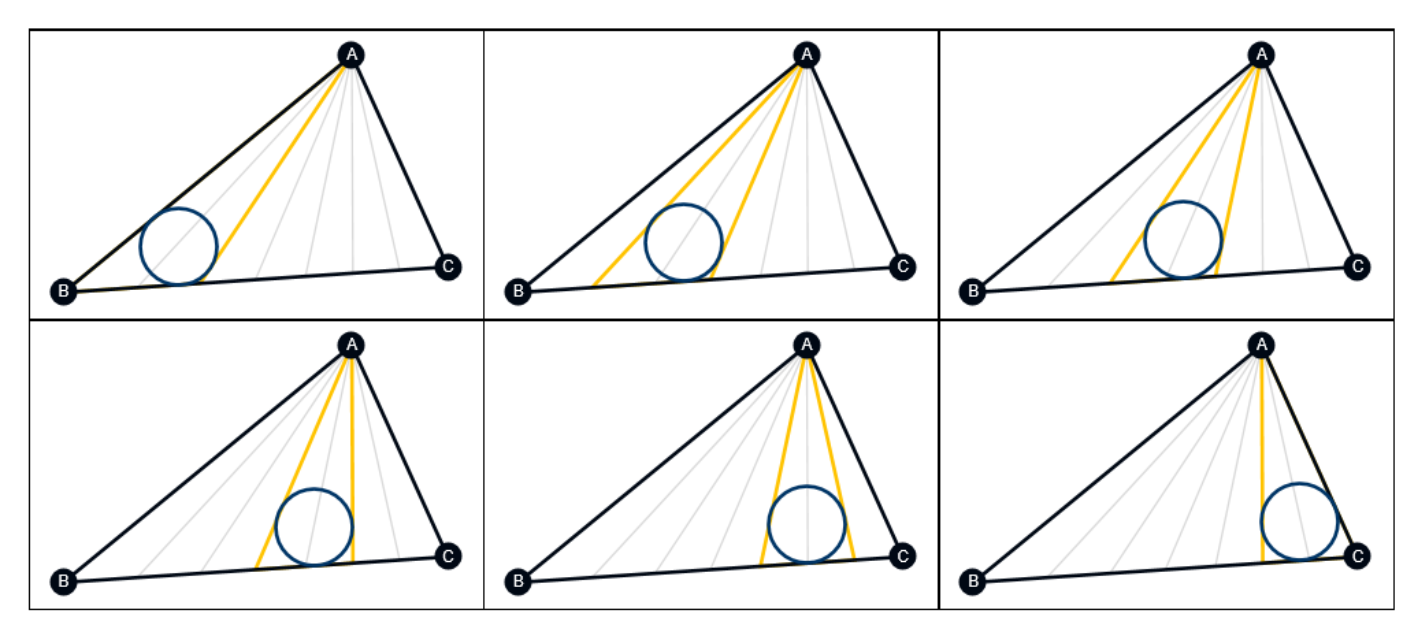

Show the same result for spanning 3 adjacent intervals:

In[24]:=
gapTri = Triangle[{vert[[1]], #1, #2}] & @@@ Table[eps[[{k, k + 3}]], {k, 1, 5}]; TriangleMeasurement[#, "Inradius"] & /@ gapTri
Out[25]=
In[26]:=
GraphicsGrid[Partition[#, UpTo@3] &@Table[ Graphics[{ {LightGray, Line[{vert[[1]], #}] & /@ eps}, {Transparent, EdgeForm[{RGBColor["#ffc300"], Thick}], tri}, {Transparent, EdgeForm[{RGBColor["#000814"], Thick}], Triangle[vert]}, {Thick, RGBColor["#003566"], TriangleConstruct[tri, "Incircle"]}, MapThread[label[#1, #2] &, {{"A", "B", "C"}, Point /@ vert}] }], {tri, gapTri}], ImageSize -> 780, Dividers -> All]
Out[26]=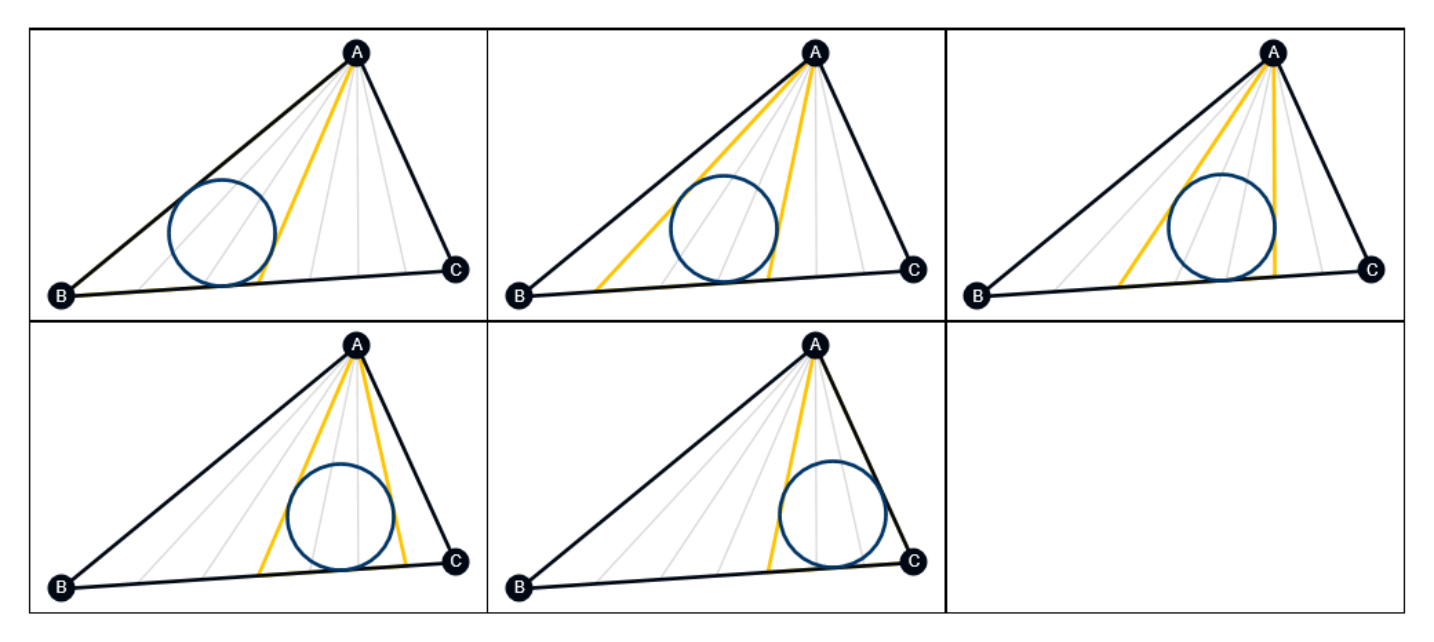

The observation follows this general argument: in triangle TSR if two cevian triangles TSU and TVR have the same inradius, so do triangles TSV and TUR:

In[27]:=
gs = GeometricScene[{\[FormalT] -> {1.3, 1.5}, \[FormalS] -> {0, 0}, \[FormalU], \[FormalV], \[FormalR] -> {2, 0}}, { Line[{\[FormalS], \[FormalU], \[FormalV], \[FormalR]}], Triangle[{\[FormalT], \[FormalS], \[FormalR]}], EuclideanDistance[\[FormalS], \[FormalU]] == 0.7, TriangleMeasurement[Triangle@{\[FormalT], \[FormalS], \[FormalU]}, "Inradius"] == TriangleMeasurement[Triangle@{\[FormalT], \[FormalV], \[FormalR]}, "Inradius"] }]; rs = RandomInstance[gs]
Out[28]=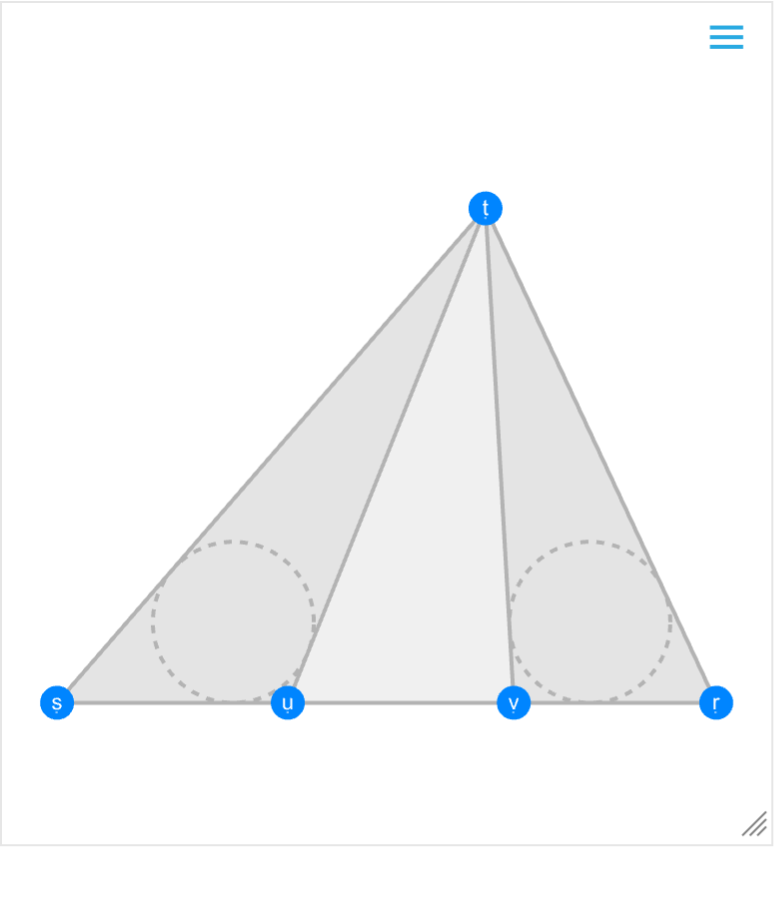

Visually verify the argument:

In[29]:=
vFun[u_?NumericQ] := vLoc /. FindRoot[ TriangleMeasurement[{{1.3, 1.5}, {u, 0}, {0, 0}}, "Inradius"] == TriangleMeasurement[{{1.3, 1.5}, {vLoc, 0}, {2, 0}}, "Inradius"], {vLoc, 2 - u}]
In[30]:=
intr = FunctionInterpolation[vFun[t], {t, 0.1, 1.9}];
In[31]:=
GraphicsRow[{ Plot[TriangleMeasurement[{{1.3, 1.5}, {intr[u], 0}, {0, 0}}, "Inradius"], {u, 0.2, 1.8}, PlotLabel -> "Inradius of TSV vs dist(SU)", AxesLabel -> {"dist(SU)", "Inradius"}], Plot[TriangleMeasurement[{{1.3, 1.5}, {u, 0}, {2, 0}}, "Inradius"], {u, 0.2, 1.8}, PlotLabel -> "Inradius of TUR vs dist(SU)", AxesLabel -> {"dist(SU)", "Inradius"}] }, ImageSize -> 720]
Out[31]=

Publisher

Shenghui Yang

Requirements

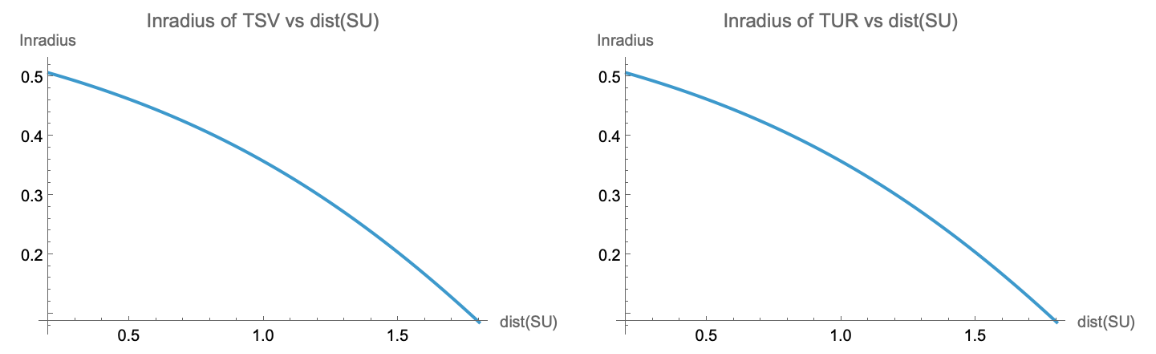Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 03 February 2025

Source Metadata

  • Citation:
    • Weisstein, Eric W. Incircle. From MathWorld--A Wolfram Web Resource.
    • Weisstein, Eric W. Congruent Incircles. From MathWorld--A Wolfram Web Resource.
    • Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, 1991.

Related Resources

License Information