Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GershgorinDisks

Source Notebook

Show the Gershgorin disks of a square matrix

Contributed by: Jan Mangaldan

ResourceFunction["GershgorinDisks"][m]

gives a Region representing the union of the Gershgorin disks of the square matrix m.

ResourceFunction["GershgorinDisks"][m,out]

gives a result of the type specified by out.

Details

"Gershgorin" is sometimes also spelled "Geršgorin" or "Gerschgorin".
The union of the Gershgorin disks encloses all the eigenvalues of the given matrix, and each eigenvalue is in at least one of the disks.
out can be any of the following:
"Region"a Region representing the union of the Gershgorin disks
"List"a list of Disk objects representing the Gershgorin disks
SparseArray objects and structured arrays can be used in ResourceFunction["GershgorinDisks"].

Examples

Basic Examples (2) 

The Gershgorin disks of a machine-precision matrix:

In[1]:=
mat = {{10., -1., 0., 1.}, {0.2, 8., 0.2, 0.2}, {1., 1., 2., 1.}, {-1., -1., -1., 12.}}; ResourceFunction["GershgorinDisks"][mat]
Out[1]=

Show the Gershgorin disks along with the eigenvalues:

In[2]:=
Show[%, ComplexListPlot[Eigenvalues[mat], PlotMarkers -> {"\[Times]", Large}, PlotStyle -> Red], Frame -> True]
Out[2]=

Scope (3) 

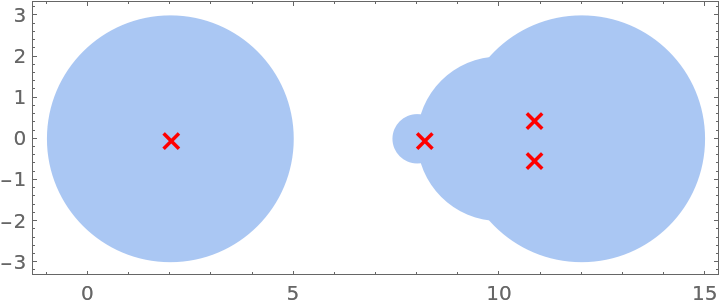Gershgorin disks of an exact matrix:

In[3]:=
ResourceFunction["GershgorinDisks"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}]
Out[3]=

List the individual disks comprising the region:

In[4]:=
ResourceFunction[ "GershgorinDisks"][{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}, "List"]
Out[4]=

Gershgorin disks of a complex matrix:

In[5]:=
ResourceFunction[ "GershgorinDisks"][{{1.2 + I, 3 - 2 I, 3 \[Pi]}, {-0.2, 5 I, 2}, {1, 2.3, E}}]
Out[5]=

List the individual disks comprising the region:

In[6]:=
ResourceFunction[ "GershgorinDisks"][{{1.2 + I, 3 - 2 I, 3 \[Pi]}, {-0.2, 5 I, 2}, {1, 2.3, E}}, "List"]
Out[6]=

Gershgorin disks of a SparseArray:

In[7]:=
ResourceFunction["GershgorinDisks"][ SparseArray[{{1, 3} -> 2., {2, 2} -> 3., {3, 1} -> 1., {4, 2} -> 5.}, {4, 4}]]
Out[7]=

Applications (3) 

Compare the Gershgorin disks of an unsymmetric matrix and its transpose:

In[8]:=
BlockRandom[SeedRandom[54321]; mat = RandomVariate[NormalDistribution[], {12, 12}, WorkingPrecision -> 25]]; {Graphics[{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mat, "List"], Last]}, Frame -> True], Graphics[{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ ResourceFunction["GershgorinDisks"][Transpose[mat], "List"], Last]}, Frame -> True]}
Out[8]=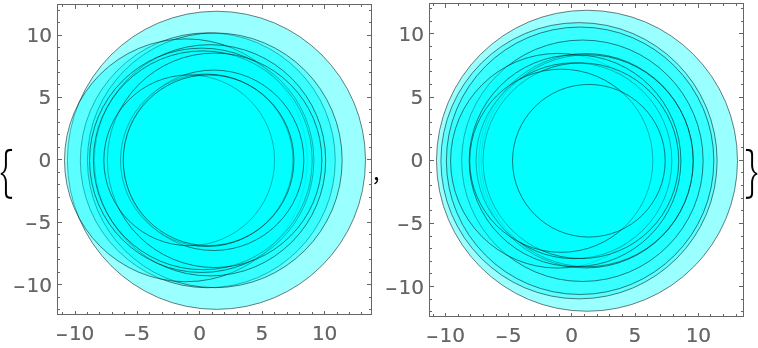

Show the intersection of the two sets of Gershgorin disks along with the eigenvalues:

In[9]:=
Show[Region[ RegionIntersection[ResourceFunction["GershgorinDisks"][mat], ResourceFunction["GershgorinDisks"][Transpose[mat]]]], ComplexListPlot[Eigenvalues[mat], PlotMarkers -> {"\[Times]", Large}, PlotStyle -> Red], Frame -> True]
Out[9]=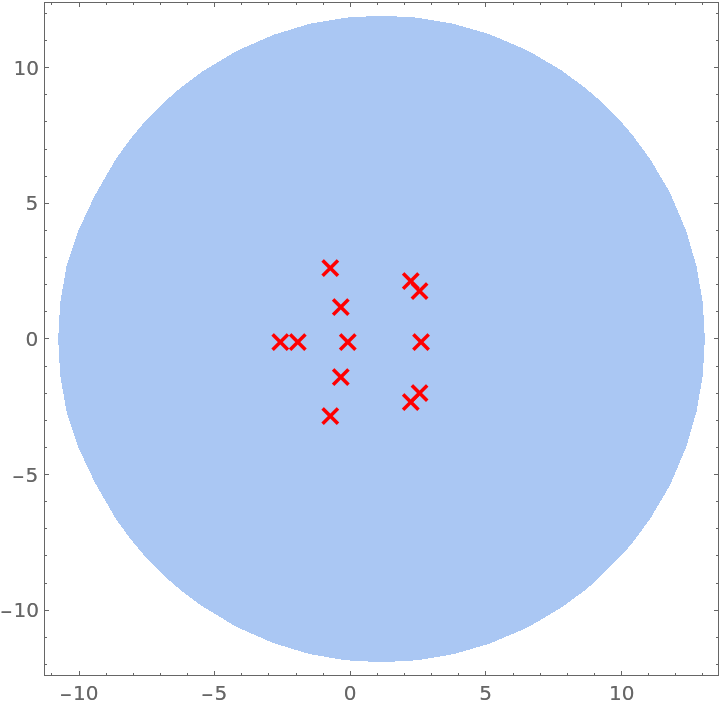

A random matrix:

In[10]:=
BlockRandom[SeedRandom[1337]; mat = RandomReal[{-9, 9}, {7, 7}]] // MatrixForm
Out[10]=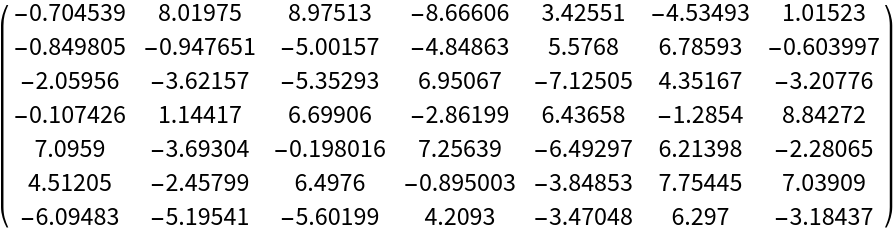

Use HessenbergDecomposition to transform it to a similar upper Hessenberg matrix:

In[11]:=
(hes = Last[HessenbergDecomposition[mat]]) // MatrixForm
Out[11]=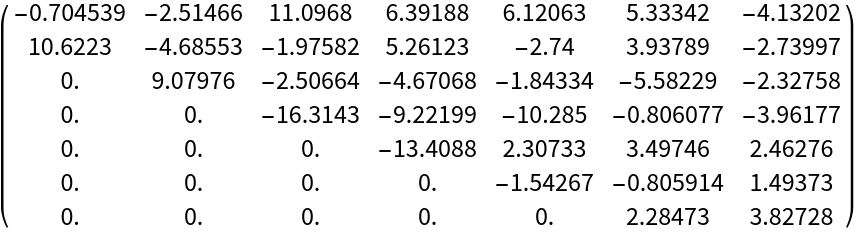

Compare the Gershgorin disks of the original and transformed matrices:

In[12]:=
eigs = Eigenvalues[hes]; {Graphics[{{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mat, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[eigs]]}}, Frame -> True], Graphics[{{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][hes, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[eigs]]}}, Frame -> True]}
Out[12]=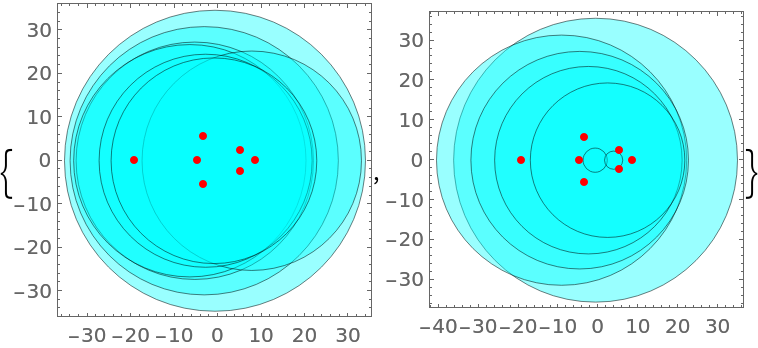

Compare the Gershgorin disks of two different companion matrices of a given polynomial:

In[13]:=
poly = 5 + 4 x + 3 x^2 + 2 x^3 + x^4 + x^5; rts = x /. NSolve[poly, x]; mfro = ResourceFunction["GeneralizedFiedlerMatrix"][Range[5, 1, -1], poly, x]; mfie = ResourceFunction["GeneralizedFiedlerMatrix"][poly, x]; {Graphics[{{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mfro, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[rts]]}}, Frame -> True, PlotLabel -> "Frobenius"], Graphics[{{Directive[ FaceForm[ Opacity[0.4, Hue[0.5]]], EdgeForm[ Directive[ Opacity[ Rational[1, 2], GrayLevel[0]], AbsoluteThickness[ Rational[1, 2]]]]], ReverseSortBy[ResourceFunction["GershgorinDisks"][mfie, "List"], Last]}, {Directive[Red, AbsolutePointSize[4]], Point[ReIm[rts]]}}, Frame -> True, PlotLabel -> "Fiedler"]}
Out[13]=

Properties and Relations (2) 

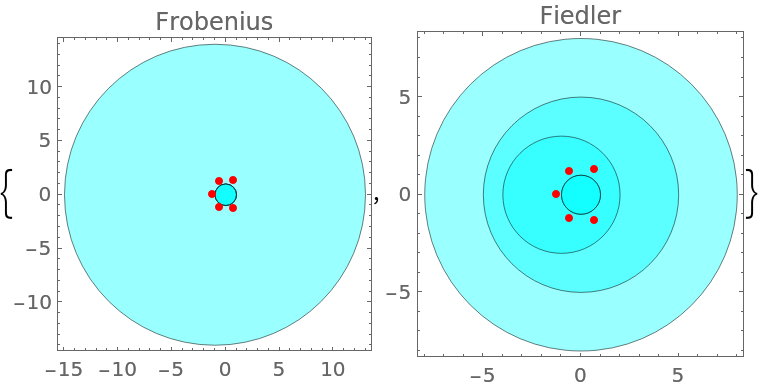The Gershgorin disks of a matrix enclose all of the matrix's eigenvalues:

In[14]:=
BlockRandom[SeedRandom[14344]; mat = RandomVariate[NormalDistribution[], {5, 5}]]; gd = ResourceFunction["GershgorinDisks"][mat]; eigs = Eigenvalues[mat]; RegionMember[gd][ReIm[eigs]]
Out[14]=

The Gershgorin disks of a diagonal matrix is a set of disks with zero radius:

In[15]:=
ResourceFunction["GershgorinDisks"][ DiagonalMatrix[{-1 - I, 0, 3 + 4 I}], "List"]
Out[15]=
In[16]:=
RegionDimension[ ResourceFunction["GershgorinDisks"][ DiagonalMatrix[{-1 - I, 0, 3 + 4 I}]]]
Out[16]=

Version History

  • 1.0.0 – 10 May 2021

Source Metadata

  • Citation:
    • Varga R.S., Geršgorin and His Circles. Berlin: Springer-Verlag, 2004.

Related Resources

License Information