Function Repository Resource:

CellularAutomataCartogram

Source Notebook

A cellular automata method for creating cartograms

Contributed by: Björn Zimmermann

ResourceFunction["CellularAutomataCartogram"][loc→val]

attempts to equalize the density of val over an area by adjusting the boundaries of loc.

ResourceFunction["CellularAutomataCartogram"][{loc₁→val₁,loc₂→val₂,…}]

attempts to equalize the density of val_i over an area by adjusting the boundaries of loc_i.

Details and Options

The original Graphics of a certain ImageSize is rasterized due to RasterSize, and subsequently the density is equalized with a cellular automata.

The original overall outer boundaries are maintained; only internal boundaries are adjusted.

The locations loc can be coordinate pairs, GeoPosition, Entity or EntityClass objects with geographic coordinates, such as cities or countries etc.

Location value pairs in Association are supported.

Initial rasterization imposes a one-pixel threshold on areas.

Areas that remain after initial rasterization will always maintain at least one pixel, and thus never disappear.

ColorFunction and ColorFunctionScaling are supported options.

The upper limit for the number of iterations can be set with MaxIterations (default 100).

Examples

Basic Examples (2)

Use a small RasterSize to reduce the number of pixels and thus speed up the calculation. Check the initial state:

In[1]:=

ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, RasterSize -> 50, MaxIterations -> 0]

Out[1]=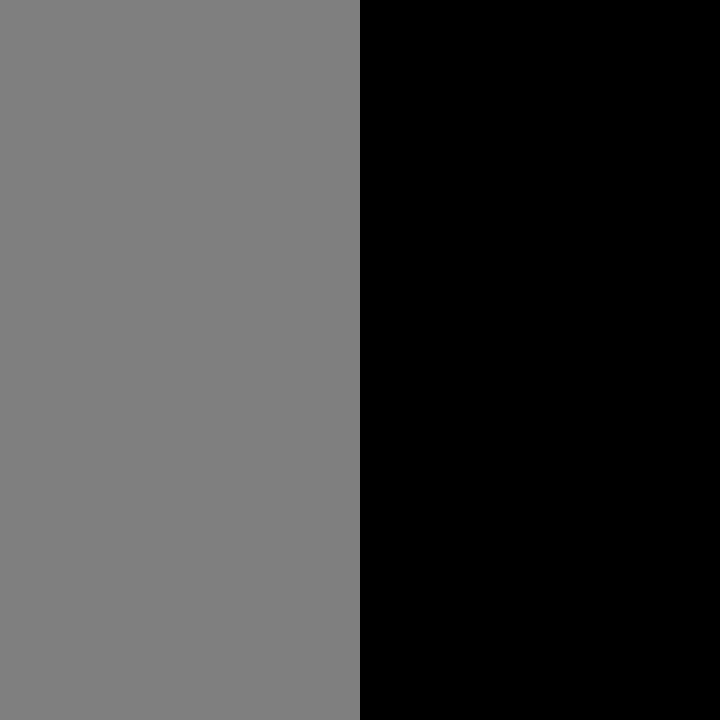

Equalize the density:

In[2]:=

res = ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, RasterSize -> 50]

Out[2]=

Check the result:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Here is the same example in a colorized version:

In[5]:=

res = ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, ColorFunction -> "Rainbow", RasterSize -> 50]

Out[5]=

Adjust the administrative division boundaries of the UK to equalize population density:

In[6]:=

UKadd1 = EntityList[
Entity["AdministrativeDivision", {EntityProperty[
"AdministrativeDivision", "ParentRegion"] -> Entity["Country", "UnitedKingdom"]}]];

In[7]:=

UKadd2 = Flatten[EntityList[
Entity["AdministrativeDivision", {EntityProperty[
"AdministrativeDivision", "ParentRegion"] -> #}]] & /@ UKadd1];

Initial state:

In[8]:=

Out[8]=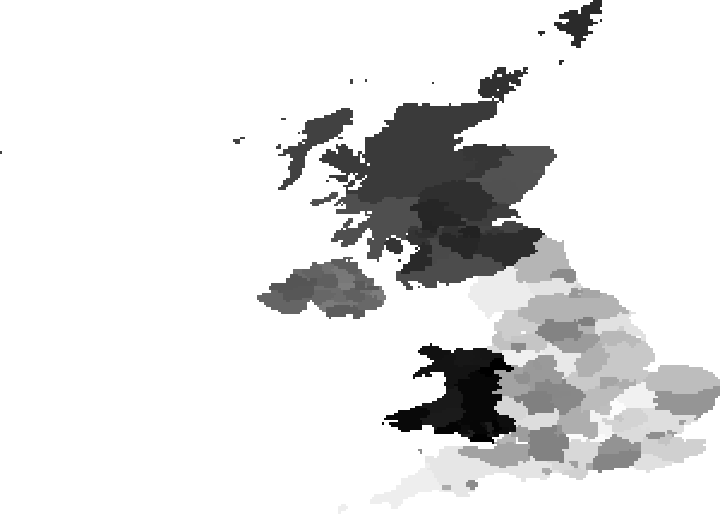

Final state after population density adaptation:

In[9]:=

Out[9]=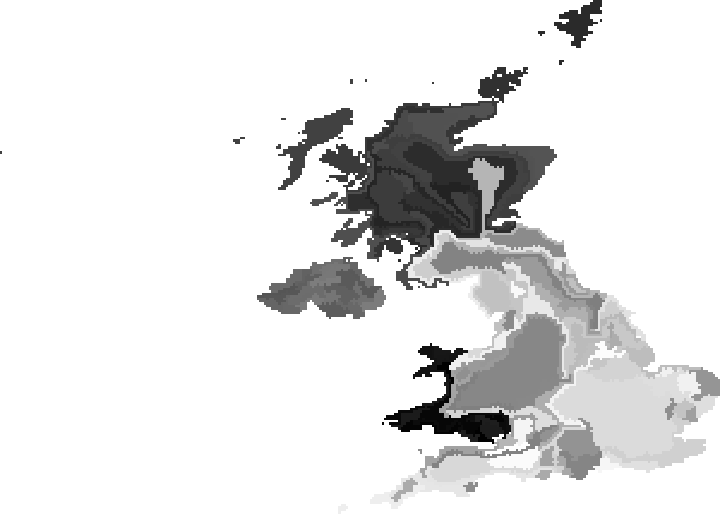

Options (4)

ImageSize (1)

Adjust the size of the image, which affects rasterization and thus the final result:

In[10]:=

ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, ImageSize -> 100]

Out[10]=

RasterSize (1)

Adjust the raster size of the image, which affects the final result:

In[11]:=

ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, RasterSize -> 100]

Out[11]=

MaxIterations (1)

The initial state is the zeroth iteration:

In[12]:=

ResourceFunction[
"CellularAutomataCartogram"][{Polygon[{{-10, -10}, {-10, 10}, {0, 10}, {0, -10}}] -> 1, Polygon[{{0, -10}, {0, 10}, {10, 10}, {10, -10}}] -> 1.1}, MaxIterations -> 0]

Out[12]=

TrackGini (1)

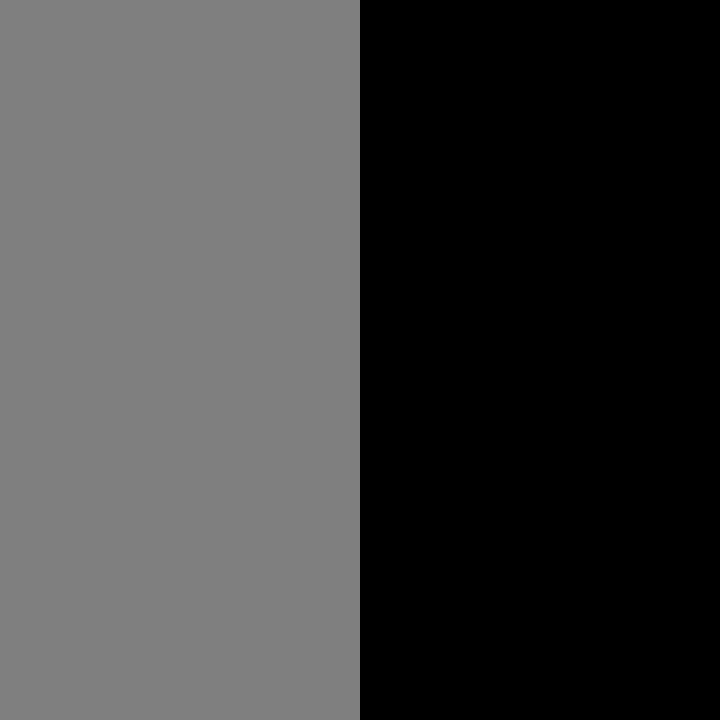The Gini coefficient is a measure of statistical dispersion. A Gini coefficient of zero expresses perfect equality, where all values are the same. A Gini coefficient of 1 expresses maximal inequality among values. The Gini coefficient is calculated each 100th iteration:

In[13]:=