Basic Examples (4) 

Start with a categorical distribution:

In[1]:=

Out[1]=

Condition that distribution on the first dimension taking on a value of "A":

In[2]:=

Out[2]=

Find the probabilities from that categorical distribution conditioned on the second dimension taking on a value of "E":

In[3]:=

Out[3]=

Use a list of patterns instead of rules to impose the same condition as above:

In[4]:=

Out[4]=

Scope (3) 

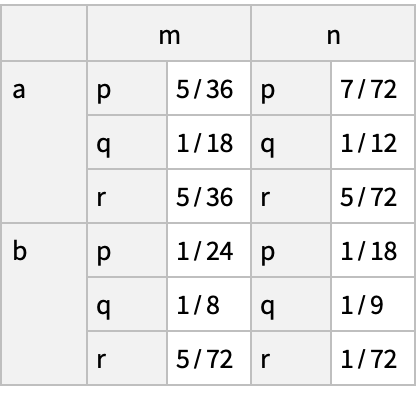
Patterns used in the conditions can be complex:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

The first category must be a letter in the word "ABLE":

In[7]:=

Out[7]=

A CategoricalDistribution of arbitrary dimension works with the function:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

The function works with univariate categorical distributions returning a CategoricalDistribution with potentially fewer categories:

In[10]:=

Out[10]=

Options (2) 

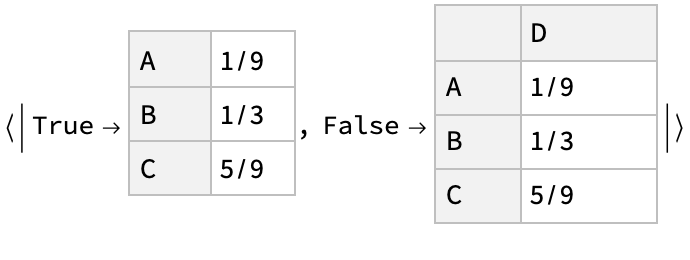
The value of the "FlattenUnivariate" option (True by default) determines whether the result of a univariate ConditionalCategoricalDistribution has its categories described without a List wrapper:

In[11]:=

Out[11]=

In[12]:=

Out[12]=

Setting the "Marginalize" option to False preserves the dimensionality of the original distribution:

In[13]:=

Out[13]=

Applications (2) 

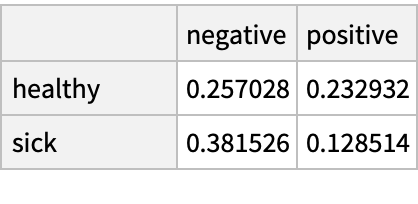
Here is the joint distribution of persons in group A or B who have or do not have some disease, and to whom a test classifies as negative or positive for the disease. Find the joint distribution of persons in group A with respect to disease and test result:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

Find the probability that a person in group A who tests positive is actually sick:

In[16]:=

Out[16]=

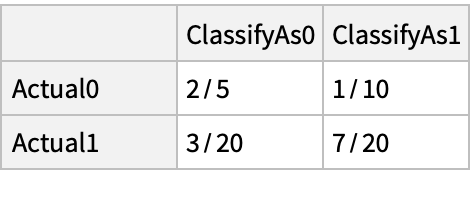
Compute the fractions of true positives (sensitivity), true negatives (specificity) and false positives (1-specificity) for a mixture of categorical distributions:

In[17]:=

In[18]:=

In[19]:=

In[20]:=

Out[20]=

In[21]:=

Out[21]=

Properties and Relations (1) 

The resource function MixtureCategoricalDistribution increases the dimensionality of a CategoricalDistribution, whereas ConditionalCategoricalDistribution reduces the dimensionality:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Neat Examples (4) 

The following application comes from the field of causal inference, which is sometimes referred to as "do-calculus". Assume the joint probability distribution of the size of a kidney stone, the treatment one receives for it and how the outcome of that treatment is distributed as set forth below:

In[24]:=

Compute the probability of a good outcome conditioned on the treatment. It will appear that B has better outcomes than A:

In[25]:=

Out[25]=

Now synthesize a randomized controlled trial and derive the interventional distribution when one forces the treatment to be "A" by computing a MixtureCategoricalDistribution over stone size in which the components are the conditional categorical distributions based on the stone size and the treatment being A:

In[26]:=

Out[26]=

Do exactly the same thing but force the treatment to be "B":

In[27]:=

Out[27]=

Although the observational distribution might suggest treatment B is superior, in fact, treatment A is superior and the observational distribution is distorted by the fact that small kidney stones, which generally have better outcomes, are more frequently treated with treatment B.