Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EvoluteCurve

Source Notebook

Compute the evolute of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["EvoluteCurve"][c,t]

computes the evolute of the curve c.

Details

An evolute is the locus of the centers of curvature of a plane curve, or the envelope of a plane curve's normals.

Examples

Basic Examples (3) 

Define the curve of an ellipse:

In[1]:=
ellipse[a_, b_, t_] := Entity["PlaneCurve", "Ellipse"][ EntityProperty["PlaneCurve", "ParametricEquations"]][a, b][t]

Compute its evolute:

In[2]:=
ResourceFunction["EvoluteCurve"][ellipse[3/2, 1, t], t] // Simplify
Out[2]=

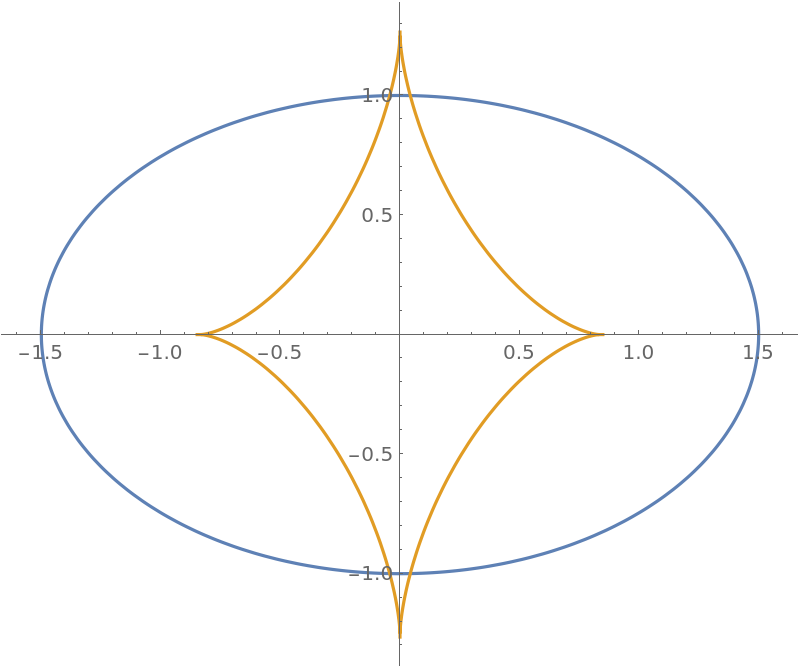
Plot the ellipse and evolute:

In[3]:=
\[Alpha] = ellipse[3/2, 1, t]; \[Epsilon] = ResourceFunction["EvoluteCurve"][\[Alpha], t]; ParametricPlot[Evaluate[{\[Alpha], \[Epsilon]}], {t, 0, 2 \[Pi]}]
Out[3]=

Define a curve known as a tractrix:

In[4]:=
tractrix[a_, t_] := a {Sin[t], Cos[t] + Log[Tan[t/2]]}

Its evolute is a catenary:

In[5]:=
ResourceFunction["EvoluteCurve"][tractrix[a, t], t] // Simplify
Out[5]=

Plot the result:

In[6]:=
\[Alpha] = tractrix[1, t]; \[Epsilon] = ResourceFunction["EvoluteCurve"][\[Alpha], t]; ParametricPlot[{\[Alpha], \[Epsilon]}, {t, 0.01, \[Pi]}, Axes -> None]
Out[6]=

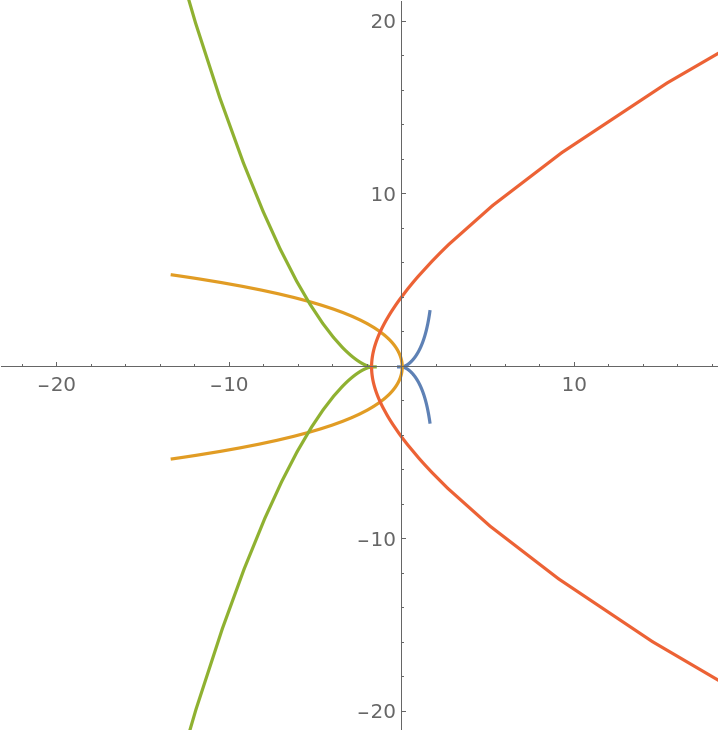
Define a curve called a cissoid:

In[7]:=
cissoid[a_, t_] := 2 a {t^2, t^3}/(1 + t^2)

Plot repeated evolutes of the curve:

In[8]:=
ParametricPlot[ Evaluate[ NestList[Simplify[ResourceFunction["EvoluteCurve"][#, t]] &, cissoid[1, t], 3]], {t, -2, 2}]
Out[8]=

Applications (2) 

Evolute of a cycloid:

In[9]:=
cycloid[a_][t_] := Entity["PlaneCurve", "Cycloid"][ EntityProperty["PlaneCurve", "ParametricEquations"]][a][t]
In[10]:=
ResourceFunction["EvoluteCurve"][cycloid[-1][t], t] // Simplify
Out[10]=

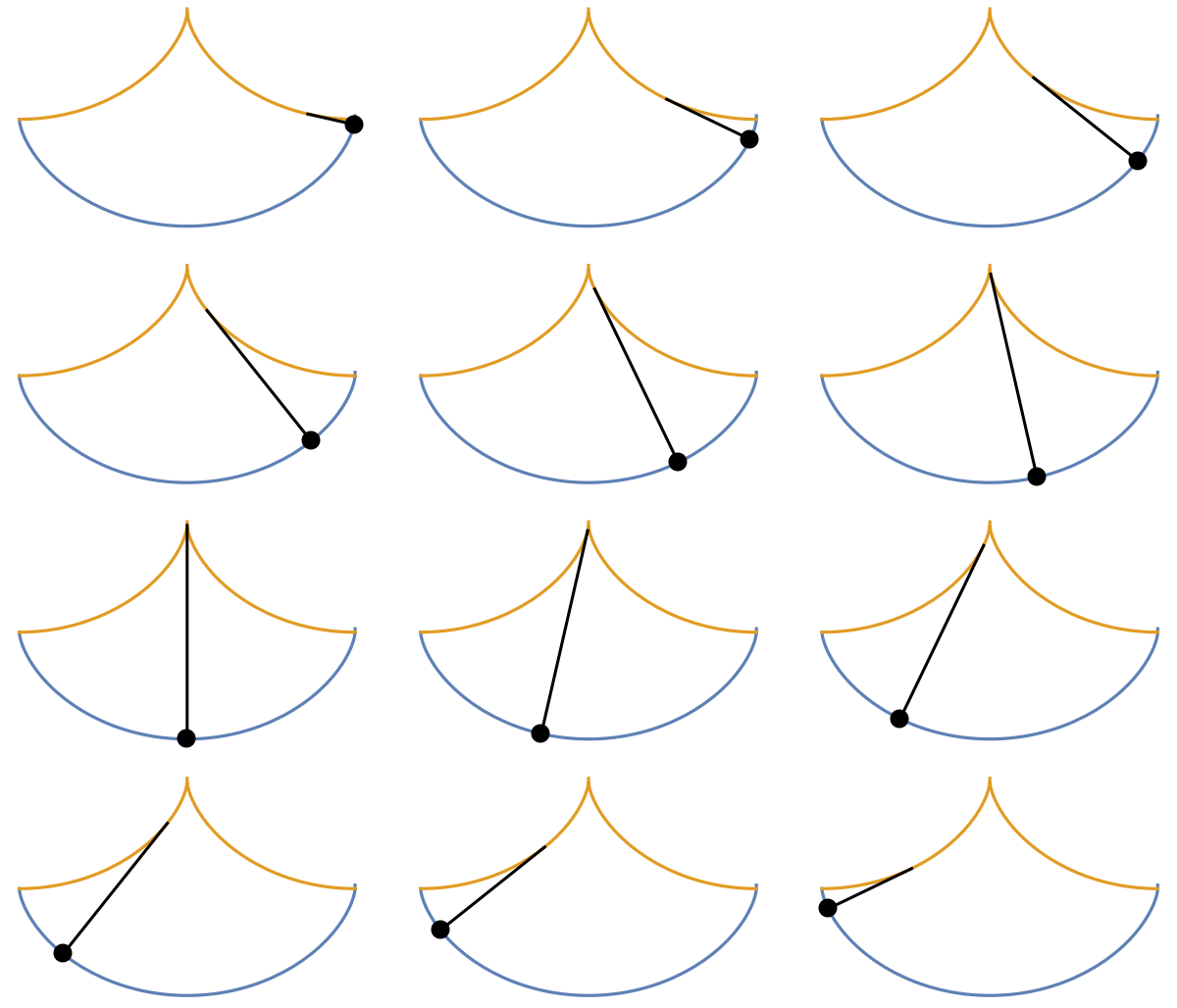
A cycloidal pendulum, which exhibits the tautochrone property:

In[11]:=
Module[{y, z}, \[Delta] = cycloid[-1]; y[a_] = {Thickness[.008], Line[{\[Delta][a], ResourceFunction["EvoluteCurve"][\[Delta][a], a]}], PointSize[.05], Point[\[Delta][a]]}; z[a_] := ParametricPlot[ Evaluate[{\[Delta][t], ResourceFunction["EvoluteCurve"][\[Delta][t], t]}], {t, -.001, 2 \[Pi] + .001}, Epilog -> y[a], Axes -> None]; GraphicsGrid[Table[z[(3 a + b) \[Pi]/7], {a, 0, 3}, {b, 3}]]]
Out[11]=

Properties and Relations (1) 

The evolute of a curve can be expressed in terms of the curvature and the normal vector:

In[12]:=
ResourceFunction["EvoluteCurve"][{f[t], g[t]}, t] == {f[t], g[t]} + ResourceFunction["NormalVector"][{f[t], g[t]}, t]/ ResourceFunction["Curvature"][{f[t], g[t]}, t] // Simplify
Out[12]=

Neat Examples (1) 

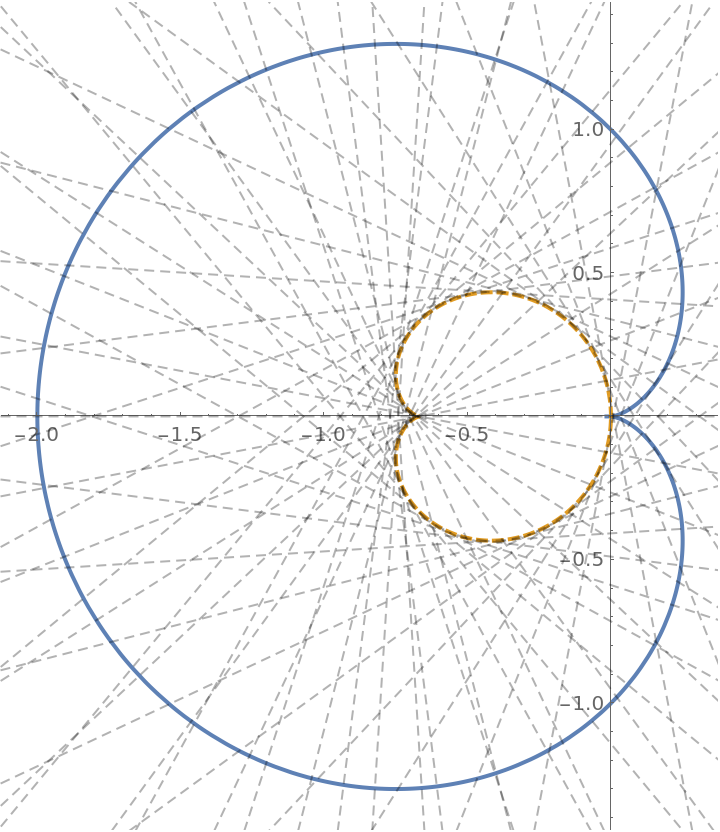
Show the evolute as an envelope of normals:

In[13]:=
cardioid[a_][t_] = Entity["PlaneCurve", "Cardioid"][ EntityProperty["PlaneCurve", "ParametricEquations"]][a][t]; cev[a_][t_] = ResourceFunction["EvoluteCurve"][cardioid[a][t], t] // Simplify; nv[a_][t_] = ResourceFunction["NormalVector"][cardioid[a][t], t] // Simplify;
In[14]:=
With[{a = 1}, ParametricPlot[{cardioid[a][t], cev[a][t]}, {t, 0, 2 \[Pi]}, PlotStyle -> {Thick, Directive[Thick, Dashed]}, Epilog -> {Directive[Opacity[0.3], Dashed], Table[InfiniteLine[cardioid[a][t], nv[a][t]], {t, \[Pi]/25, 2 \[Pi] - \[Pi]/25, \[Pi]/25}]}]]
Out[14]=

Publisher

Enrique Zeleny

Version History

  • 1.0.1 – 08 March 2021
  • 1.0.0 – 03 March 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information