Basic Examples (5)
Create a Hankel matrix:
Check that it is Hermitian:
Compute the LDL decomposition:
Check that these matrices are lower triangular with ones on the main diagonal, and diagonal respectively:
Check that we recover the original hmat from the LDL product:
Scope (3)
LDLDecomposition works with complex Hermitian matrices:
Compute the LDL decomposition:
Check that these matrices have the required properties:
Check that we recover the original matrix:
LDLDecomposition works with exact numeric matrices:
Compute the LDL decomposition:
Check that these matrices have the required properties:
Check that we recover the original matrix:
LDLDecomposition works with symbolic matrices provided it can determine that they are Hermitian:
Check that mat is Hermitian:
Compute the LDL decomposition:
Check that we recover the original matrix:
Properties and Relations (2)
Create a Hilbert matrix of dimension 5:
Check that it is positive definite:
Compute the LDL decomposition:
Check that this agrees with the rational Cholesky decomposition up to numeric machine precision error:
For positive definite matrices one can obtain the LDL decomposition from the LU decomposition (when no pivoting was performed) and also from the Cholesky decomposition. Form a positive definite matrix:
Check that the LUDecomposition did not permute any rows:
Extract the diagonal and use it to form a lower triangular matrix with ones on the main diagonal:
Check that this recovers the LDL decomposition:
Compute the CholeskyDecomposition:
Extract the diagonal and modify the Cholesky upper triangular matrix to recover the LDL decomposition:


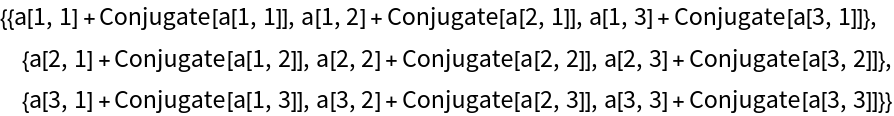


![{l2, d2} = ResourceFunction["RationalCholeskyDecomposition"][hilb];
d2 = DiagonalMatrix[d2];
Chop[{l1 - l2, d1 - d2}]](https://www.wolframcloud.com/obj/resourcesystem/images/3eb/3ebcd2b1-f522-4d6c-b7f3-68c4dac8785a/389f044f3e47a7f1.png)
![uu = UpperTriangularize[lud[[1]]];
dd = Diagonal[uu];
{ll, dd} = {Transpose[DiagonalMatrix[1/dd] . uu], DiagonalMatrix[dd]}](https://www.wolframcloud.com/obj/resourcesystem/images/3eb/3ebcd2b1-f522-4d6c-b7f3-68c4dac8785a/63f2bdf59d1cc104.png)
![diag = Diagonal[chmat];
lower = ConjugateTranspose[chmat/diag];
{ll, dd} == {lower, DiagonalMatrix[diag^2]}](https://www.wolframcloud.com/obj/resourcesystem/images/3eb/3ebcd2b1-f522-4d6c-b7f3-68c4dac8785a/46f5ffecca5b4af2.png)