Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Incrementally select elements in parallel from a list or infinite range that satisfy a predicate
ResourceFunction["IncrementalParallelSelect"][list,crit] computes Select[list,crit] in parallel and returns partial results when aborted. | |
Search for Mersenne primes in the range 1 to 1200:
| In[1]:= |
| Out[1]= |
Search for Mersenne primes with no upper limit, until aborted:
| In[2]:= |
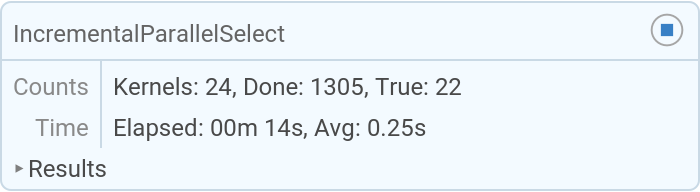
| Out[2]= |
The "Results" opener in the temporary progress display allows one to see the results as they are found:
| In[3]:= |
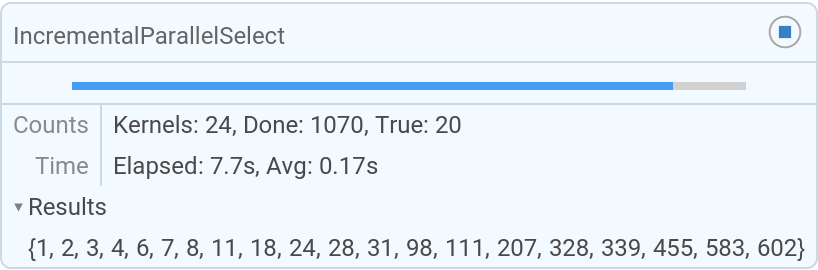
| Out[3]= |
When aborting a computation with the stop button, the number of evaluations that are still running is displayed:
| In[4]:= |

| Out[4]= |
Aborting with Evalutation ▶ AbortEvaluation terminates more quickly:
| In[5]:= |
| Out[5]= |
By default, definitions in the current context are distributed automatically:
| In[6]:= |
| In[7]:= |
| Out[7]= |
Do not distribute any definitions of functions. In this case, the definition of local is applied only after the results are returned to the local kernel:
| In[8]:= |
| In[9]:= |
| Out[9]= |
IncrementalParallelSelect returns the same result as Select, or its parallelized, non-incremental version:
| In[10]:= |
| Out[10]= |
The standard parallel version cannot return partial results when aborted:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License