Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the shape operator on a surface
ResourceFunction["ShapeOperator"][s,{u,v}] computes the shape operator of surface s with respect to variables u and v. |
Shape operator on the sphere:
| In[1]:= |
|
| In[2]:= |
|
| Out[2]= |
|
The monkey saddle:
| In[3]:= |
|
| In[4]:= |
|
| Out[4]= |
|
The shape operator:
| In[5]:= |
|
| Out[5]= |
|
A paraboloid:
| In[6]:= |
|
| In[7]:= |
|
The shape operator:
| In[8]:= |
|
| Out[8]= |
|
Alternatively, the resource function UnitNormal can be used to compute the shape operator:
| In[9]:= |
|
| Out[9]= |
|
The Weingarten matrix can be computed using the shape operator with the metric:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
Check the calculation:
| In[12]:= |
|
| Out[12]= |
|
A Monge patch:
| In[13]:= |
|
Gaussian and mean curvatures:
| In[14]:= |
|
| Out[14]= |
|
| In[15]:= |
|
| Out[15]= |
|
The shape operator:
| In[16]:= |
|
| Out[16]= |
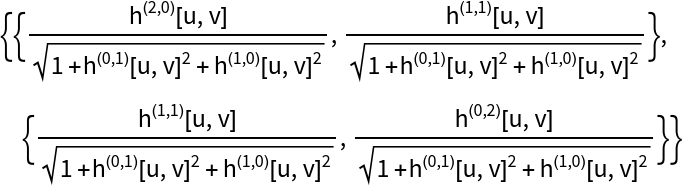
|
This work is licensed under a Creative Commons Attribution 4.0 International License