Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the Prüfer code associated with a labeled tree
ResourceFunction["LabeledTreeToPruferCode"][g] gives the Prüfer code associated with the labeled tree g. |
The Prüfer code of a labeled tree:
| In[1]:= | ![ResourceFunction["LabeledTreeToPruferCode"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 4, 3, 5, 6}, {Null, {{1, 2}, {2, 3}, {2, 4}, {4, 5}, {4, 6}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{0., 0.8164965809277261}, {
0.8164965809277261, 1.6329931618554523`}, {
0.8164965809277261, 0.8164965809277261}, {
1.6329931618554523`, 0.8164965809277261}, {
1.2247448713915892`, 0.}, {2.041241452319315, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {2, 3}, {2, 4}, {4, 5}, {4, 6}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.022945218072026957], DiskBox[2, 0.022945218072026957], DiskBox[3, 0.022945218072026957], DiskBox[4, 0.022945218072026957], DiskBox[5, 0.022945218072026957], DiskBox[6, 0.022945218072026957]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/324/324dcb1e-bf92-4b24-b6c3-3d6564201eb3/4488999ad20ea367.png) |
| Out[1]= |
Use FromDigits to obtain an integer-valued Prüfer code:
| In[2]:= |
| Out[2]= | 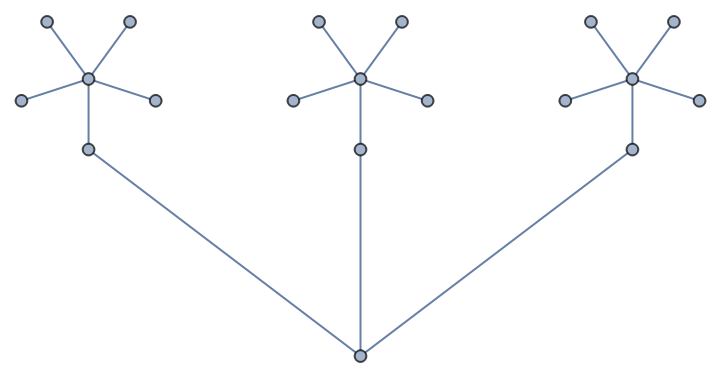 |
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
For a tree with n vertices, the length of the Prüfer code is n-2:
| In[5]:= |
| Out[5]= | 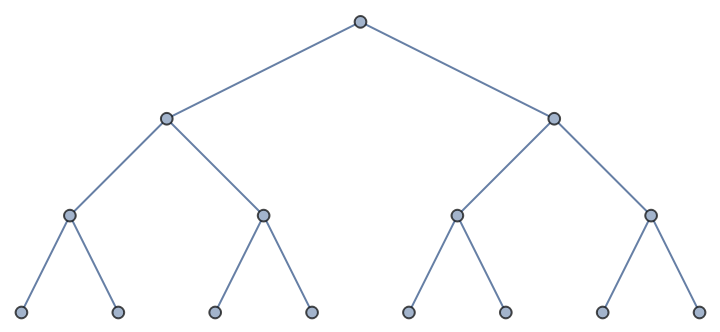 |
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
Empty Prüfer code corresponds to a tree with only two leaves:
| In[8]:= |
| Out[8]= |
The resource function PruferCodeToLabeledTree can be used to reconstruct the tree from its Prüfer code:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |  |
The Prüfer code of a path is a sequence of n-2 distinct integers:
| In[11]:= |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
The Prüfer code for an n-pointed star with the center vertex k is a sequence of n-1 copies of k:
| In[14]:= |
| Out[14]= | 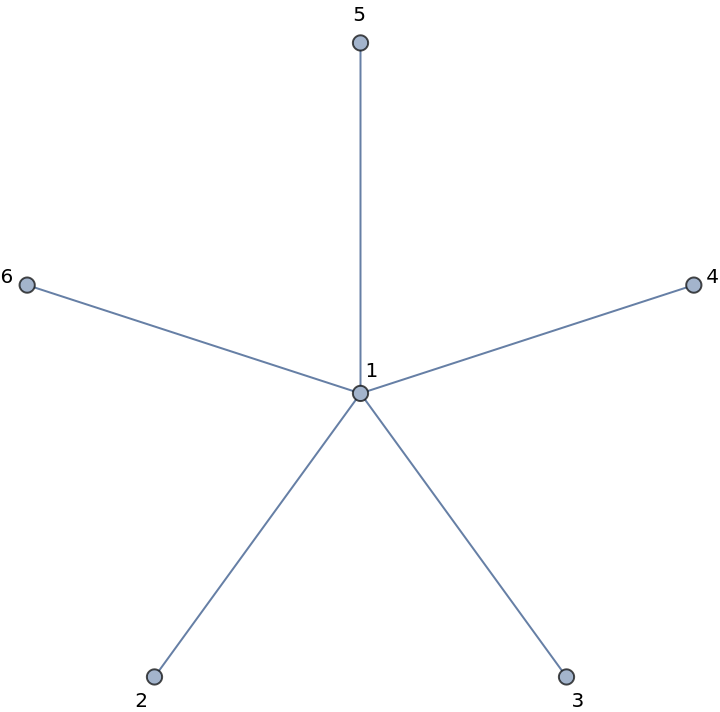 |
| In[15]:= |
| Out[15]= |
LabeledTreeToPruferCode does not work on non-explicit trees:
| In[16]:= |
| Out[16]= |
Substitute numbers for symbolic values to find the Prüfer code:
| In[17]:= |
| Out[17]= | 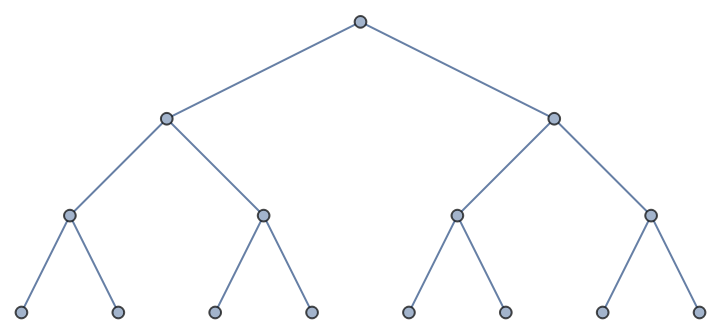 |
| In[18]:= |
| Out[18]= |
LabeledTreeToPruferCode accepts only trees with vertices numbered sequentially, starting from 1:
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
Normalize labeling:
| In[21]:= |
| Out[21]= |
| In[22]:= |
| Out[22]= |
This work is licensed under a Creative Commons Attribution 4.0 International License