Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct a labeled tree given its Prüfer code
ResourceFunction["PruferCodeToLabeledTree"][{i1,…,in-2}] gives the labeled tree on n vertices associated with the Prüfer code {i1,…,in-2}. |
The labeled tree associated with a Prüfer code:
| In[1]:= |
| Out[1]= | 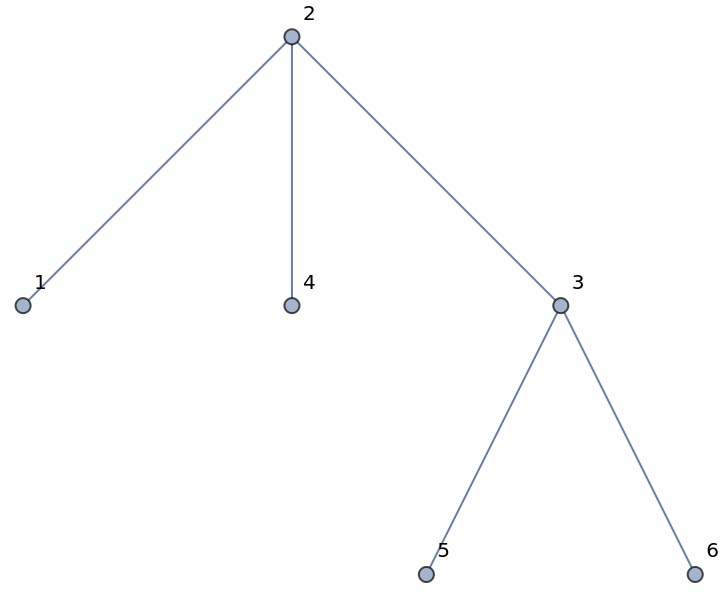 |
Do not show labels:
| In[2]:= |
| Out[2]= | 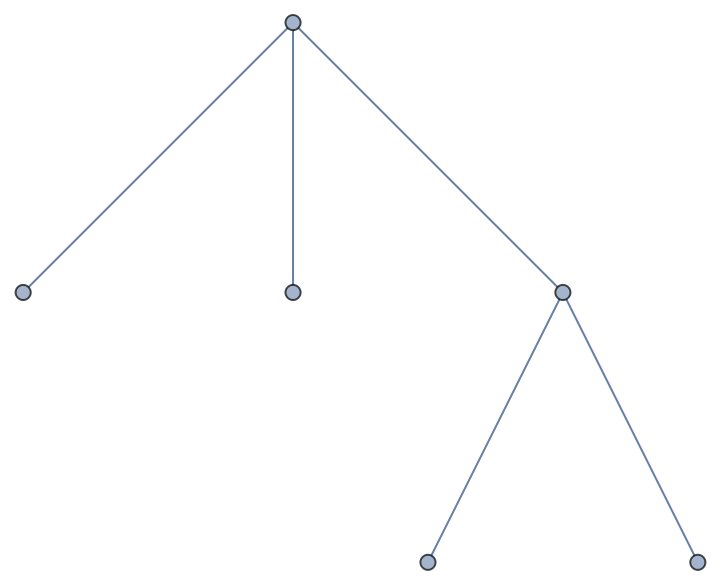 |
Generate a random tree on n vertices:
| In[3]:= |
| In[4]:= |
| Out[4]= | 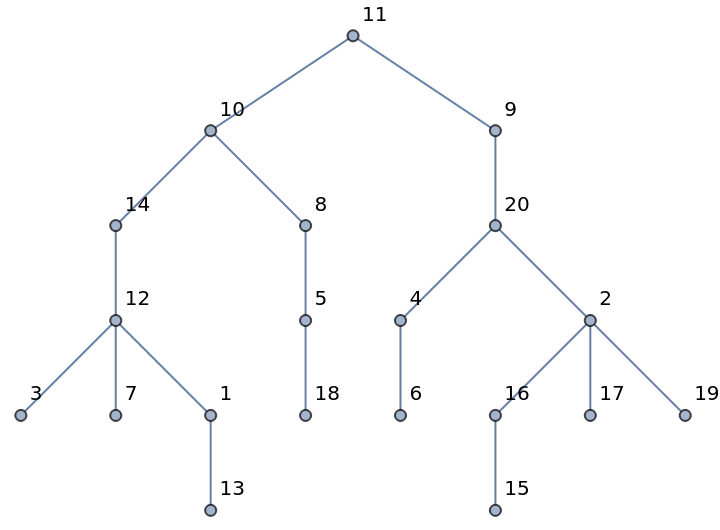 |
Count distinct unlabeled trees on n vertices:
| In[5]:= |
| In[6]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |
The tree associated with a Prüfer code of length n has n+2 vertices:
| In[8]:= |
| Out[8]= | 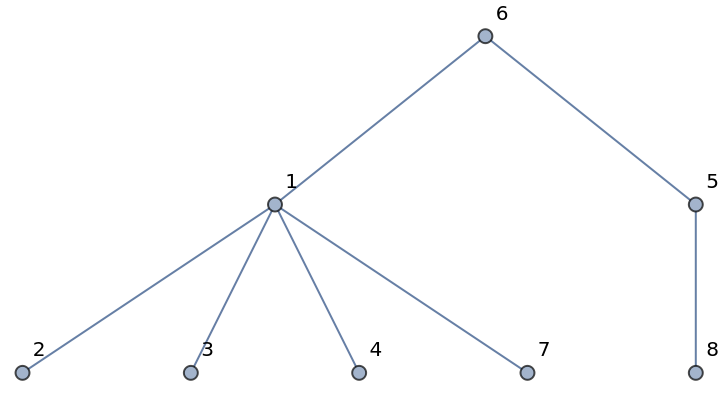 |
There are nn-2 tuples of length n−2 on the labels 1 to n and, correspondingly, the same number of different labeled trees:
| In[9]:= |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= | 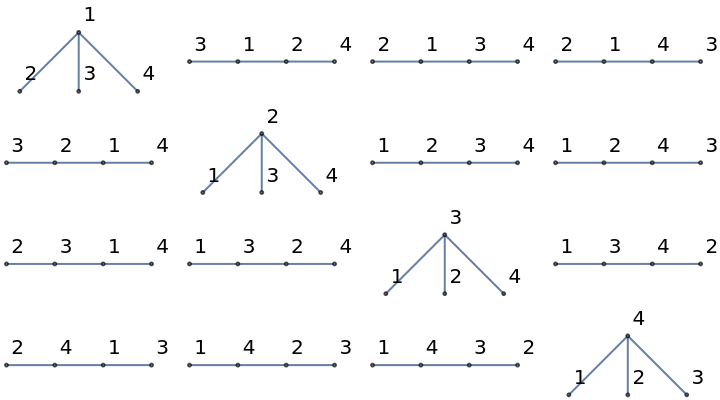 |
Empty Prüfer code corresponds to a tree with only two leaves:
| In[13]:= |
| Out[13]= |
The resource function LabeledTreeToPruferCode can be used to get the Prüfer code of a labeled tree:
| In[14]:= |
| Out[14]= | 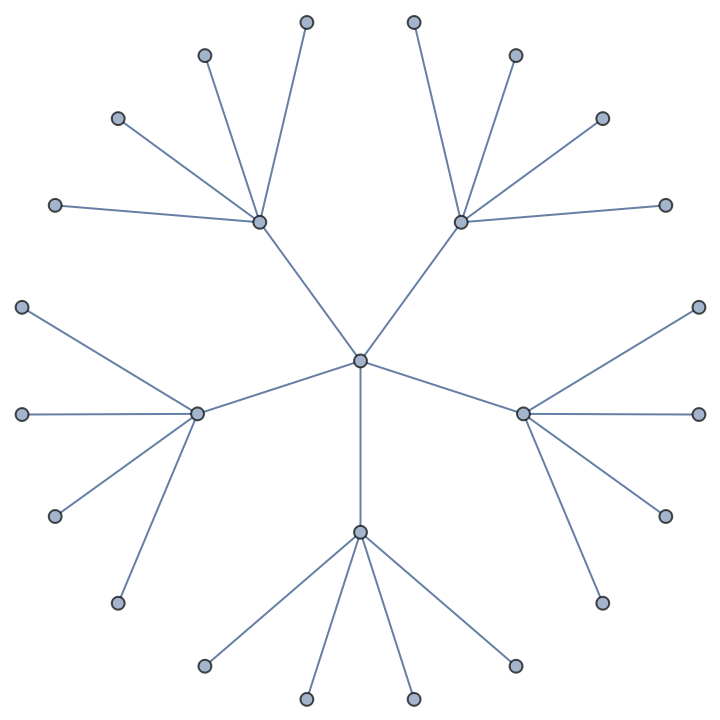 |
| In[15]:= |
| Out[15]= |
PruferCodeToLabeledTree reconstructs the tree:
| In[16]:= |
| Out[16]= | 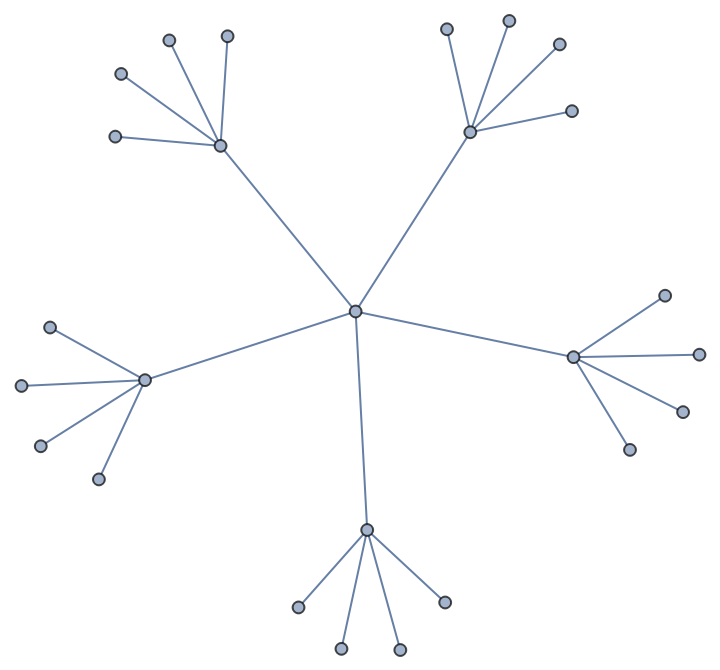 |
Composition of the resource function LabeledTreeToPruferCode and PruferCodeToLabeledTree is an identity operation for any valid value of Prüfer's code:
| In[17]:= |
| In[18]:= |
| Out[18]= | 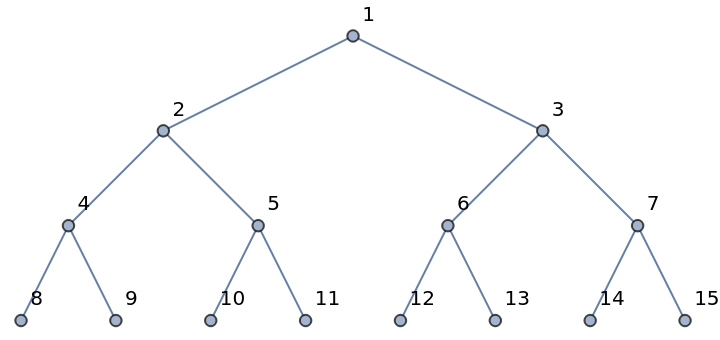 |
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
The Prüfer code of a path is a sequence of n-2 distinct integers:
| In[21]:= |
| In[22]:= |
| Out[22]= |
A sequence of n-1 copies of k is the Prüfer code for an n-pointed star with the center vertex k:
| In[23]:= |
| Out[23]= | 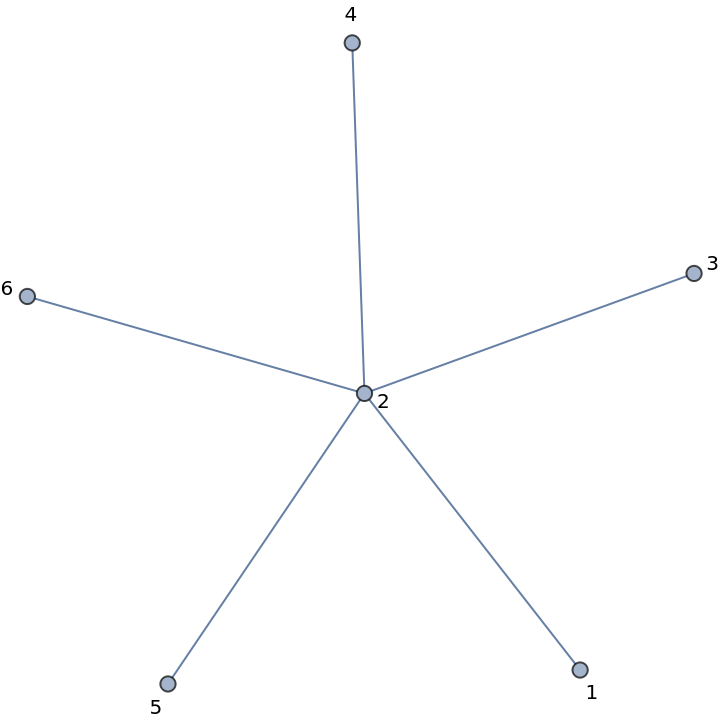 |
Integer inputs are also accepted:
| In[24]:= |
| Out[24]= | 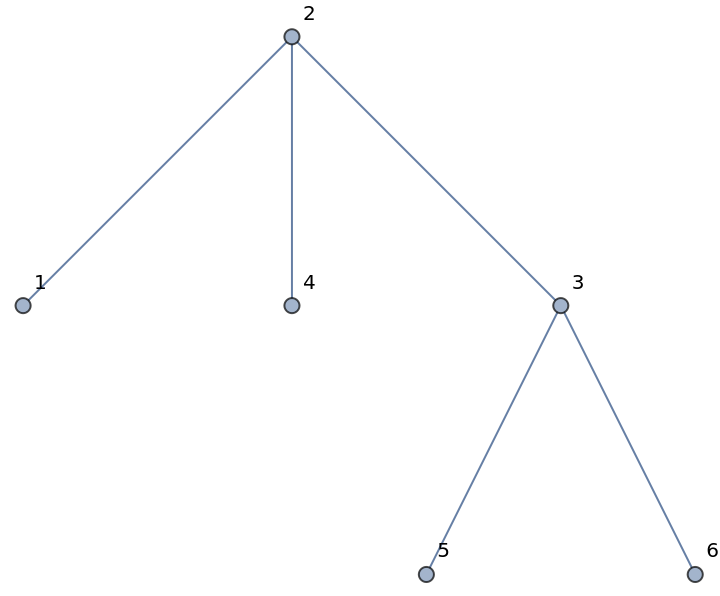 |
The result is equivalent to using the digits of the integer:
| In[25]:= |
| Out[25]= | 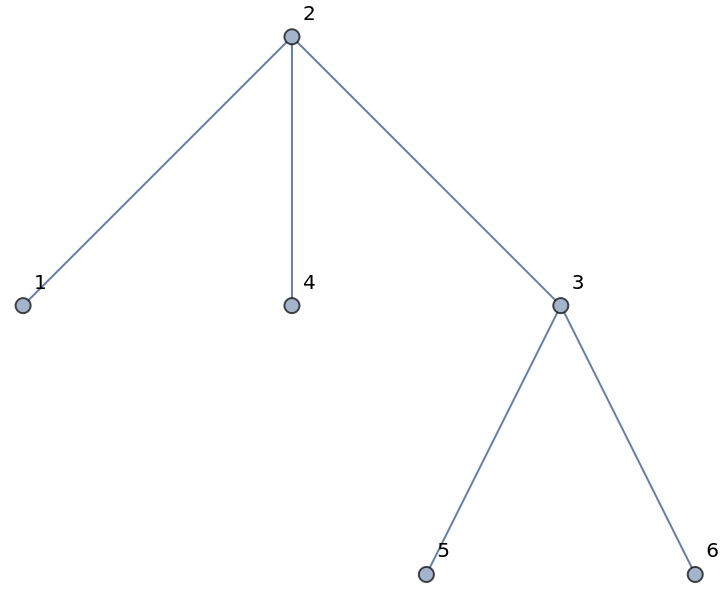 |
This work is licensed under a Creative Commons Attribution 4.0 International License