Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the Hurwitz matrix of a univariate polynomial
ResourceFunction["HurwitzMatrix"][poly,x] gives the Hurwitz matrix of poly, treated as a polynomial in x. |
Generate the Hurwitz matrix of a polynomial:
| In[1]:= |
| Out[1]= | 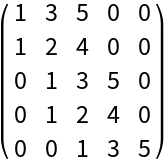 |
Generate the Hurwitz matrix from a polynomial with numeric coefficients:
| In[2]:= |
| Out[2]= |  |
Generate the Hurwitz matrix from a polynomial with symbolic coefficients:
| In[3]:= |
| Out[3]= |  |
Use HurwitzMatrix to check the stability of a polynomial:
| In[4]:= | ![poly = 1 + x/2 + x^2/9 + x^3/72 + x^4/1008 + x^5/30240;
MatrixForm[ma = ResourceFunction["HurwitzMatrix"][poly, x]]](https://www.wolframcloud.com/obj/resourcesystem/images/2e4/2e4af227-d008-4d84-8a32-f8f8f3dee90f/0d9739d65dd12b8a.png) |
| Out[4]= |  |
| In[5]:= |
| Out[5]= |
Verify stability by computing the roots of the polynomial:
| In[6]:= |
| Out[6]= |
A polynomial whose roots all have negative real parts:
| In[7]:= |
The corresponding Hurwitz matrix has principal minors that are all positive:
| In[8]:= |
| Out[9]= |
Apply a Möbius transformation to the polynomial:
| In[10]:= |
| Out[10]= |
The transformed polynomial has a Schur matrix that is positive definite. That is, all of the roots of the transformed polynomial are within the unit disk:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License