Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 OsculatingConic

Source Notebook

Get the osculating conic of a plane curve

Contributed by: Jan Mangaldan

ResourceFunction["OsculatingConic"][c,{t,t0},{x,y}]

gives the implicit equation with variables x and y for the osculating conic of a plane curve c depending on parameter t at t=t0.

Details

The osculating conic of a plane curve at a given point is the unique conic that has fourth-order contact with the curve at that point.

Examples

Basic Examples (2) 

The implicit Cartesian equation for the osculating conic of a deltoid:

In[1]:=
conic = ResourceFunction["OsculatingConic"][ Entity["PlaneCurve", "Deltoid"]["ParametricEquations"][1][ t], {t, \[Pi]/6}, {x, y}] // Simplify
Out[1]=

Plot the deltoid and its osculating conic along with their point of contact:

In[2]:=
Show[ParametricPlot[ Evaluate[ Entity["PlaneCurve", "Deltoid"]["ParametricEquations"][1][t]], {t, 0, 2 \[Pi]}, PlotStyle -> Thick], ContourPlot[Evaluate[conic], {x, -3/2, 3/2}, {y, -3/2, 3/2}, ContourStyle -> ColorData[97, 2], PlotPoints -> 105], Epilog -> {Red, AbsolutePointSize[4], Point[Entity["PlaneCurve", "Deltoid"]["ParametricEquations"][ 1][\[Pi]/6]]}, PlotRange -> All]
Out[2]=

Scope (2) 

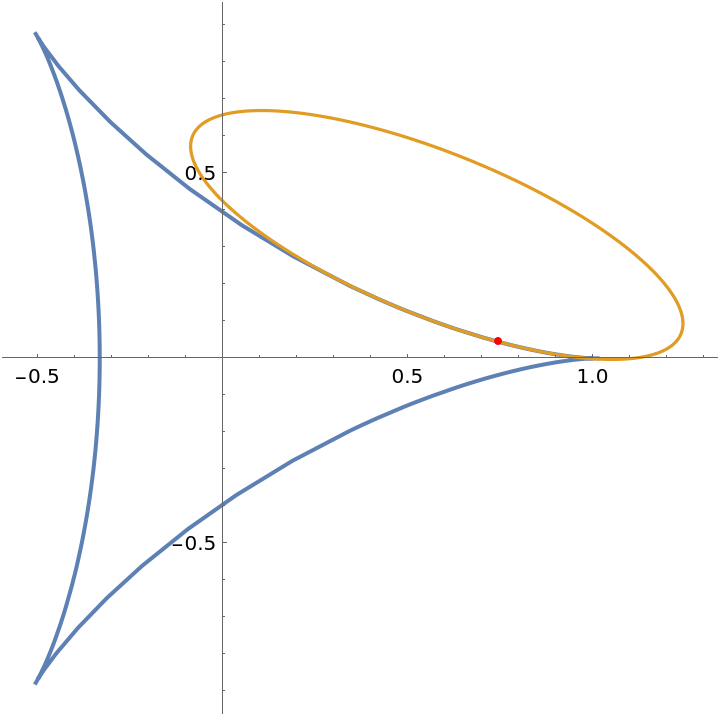The osculating conic for a catenary:

In[3]:=
conic = FullSimplify[ ResourceFunction["OsculatingConic"][{t, Cosh[t]}, {t, t0}, {x, y}], t0 \[Element] Reals]
Out[3]=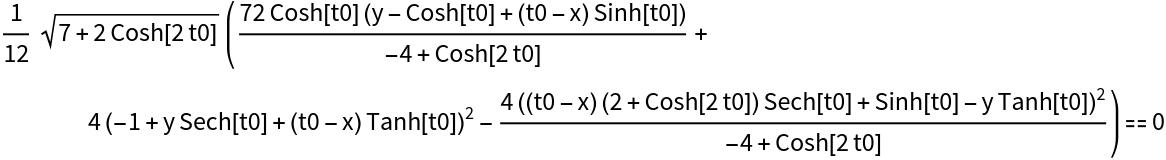

Show three of the osculating conics along with the catenary:

In[4]:=
Legended[ Show[Plot[Cosh[x], {x, -7, 7}, PlotStyle -> Directive[AbsoluteThickness[4], ColorData[97, 4]]], ContourPlot[{conic /. t0 -> -1/2, conic /. t0 -> Log[(Sqrt[10] - Sqrt[6])/2], conic /. t0 -> 2} // Evaluate, {x, -25, 25}, {y, -25, 25}, ContourStyle -> Directive[AbsoluteThickness[2], Dashed]], AspectRatio -> Automatic, PlotRange -> 25], LineLegend[ Array[Directive[ColorData[97, #], AbsoluteThickness[2], Dashed] &, 3], {"ellipse", "parabola", "hyperbola"}]]
Out[4]=

Properties and Relations (1) 

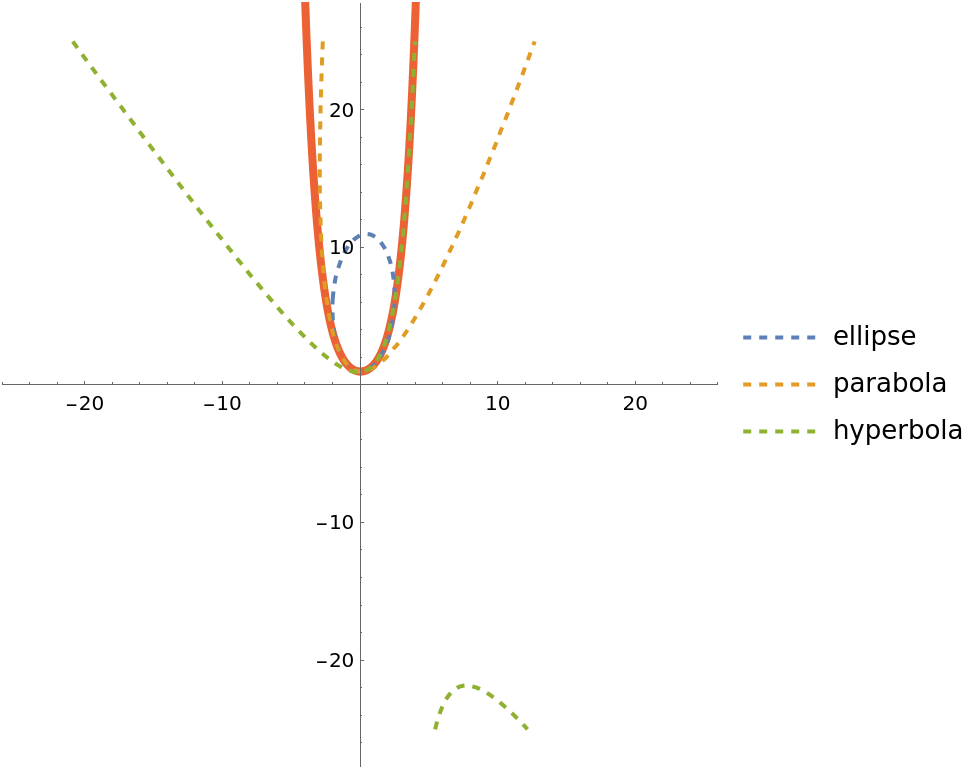Use the resource function ConicProperties to get further information on an osculating conic:

In[5]:=
conic = ResourceFunction["OsculatingConic"][ Entity["PlaneCurve", "Lemniscate"]["ParametricEquations"][1][ t], {t, 0}, {x, y}] // Simplify
Out[5]=
In[6]:=
ResourceFunction["ConicProperties"][conic, {x, y}]
Out[6]=

Version History

  • 1.0.0 – 08 March 2021

Source Metadata

  • Citation:
    • Gordon, R. A., "The Aberrancy of Plane Curves." The Mathematical Gazette, vol. 89, no. 516, 424–436, 2005 DOI: 10.1017/S0025557200178271
    • Schot, S. H., "Aberrancy: Geometry of the Third Derivative." Mathematics Magazine, vol. 51, no. 5, 259–275, 1978. DOI: 10.1080/0025570X.1978.11976728
    • Walker, A., "The differential equation of a conic and its relation to aberrancy." American Mathematical Monthly, vol. 59, 531–539, 1952. DOI: 10.1080/00029890.1952.11988184

Related Resources

License Information