Function Repository Resource:

ConicProperties

Get an association of the properties of a conic section

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["ConicProperties"][expr,{x,y}]

returns an association of properties of expr, if expr defines a conic section, with respect to variables x and y.

Details

The input expr can be an equation or an Association of properties of a conic section with respect to the variables x and y.

The three distinct, non-degenerate conic sections are parabolas, hyperbolas and ellipses, with circles as a special case of an ellipse.

Parabola properties returned are: "Equation", "Focus ", "Vertex", "Directrix", "FocalParameter", "SemiAxisLength", "AxisOfSymmetry", "SemiLatusRectum", "RotationAngle" and "BaseConic".

Ellipse properties returned are: "Equation", "Foci", "Vertices", "Covertices", "Eccentricity", "Center", "SemimajorAxisLength", "SemiminorAxisLength", "AreaEnclosed", "SemiLatusRectum", "Directrices", "AxesOfSymmetry", "Circumference", "RotationAngle" and "BaseConic".

Circle properties returned are: "Equation", "Radius", "Circumference", "Center" and "AreaEnclosed".

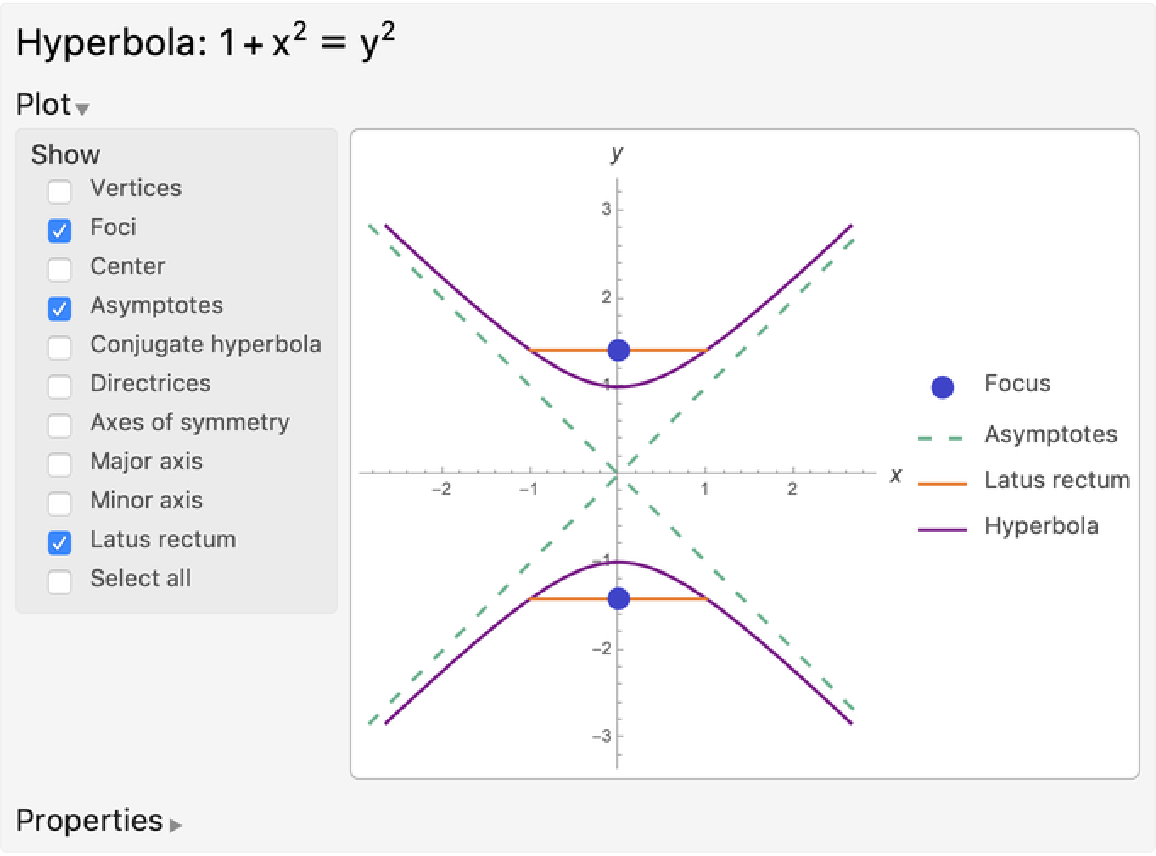
Hyperbola properties returned are: "Equation", "Foci", "Vertices", "Eccentricity", "Asymptotes", "Center", "SemimajorAxisLength", "SemiminorAxisLength", "Directrices", "AxesOfSymmetry", "SemiLatusRectum", "RotationAngle", "ConjugateHyperbola" and "BaseConic".

For parabolas, ellipses and hyperbolas, the "BaseConic" property is an association of the properties "Equation", "RotationAngle" and "DisplacementFromOrigin" where "Equation" represents an isomorphic conic section based at the origin and aligned with the x axis.

Examples

Basic Examples (1)

Compute the properties of a conic section from its equation:

In[1]:=

$ResourceFunction["ConicProperties"][1 + x^2 == y^2, {x, y}]$

Out[1]=

Scope (2)

Provide an association of properties for an unknown conic section and compute the full association of properties, including the type of conic section:

In[2]:=

Out[2]=

In[3]:=

Out[3]=

The equation of the conic section may contain symbolic parameters; the properties of a general conic section centered at {h, k} with semi-axis lengths a and b:

In[4]:=

$Assuming[a > 0 && b > 0, ResourceFunction[ "ConicProperties"][(x - h)^2/a^2 - (y - k)^2/b^2 == 1, {x, y}]]$

Out[4]=

Properties and Relations (2)

Compute some properties of a hyperbola:

In[5]:=

$ResourceFunction["ConicProperties"][ 1 + x^2 == y^2, {x, y}] /@ {"Foci", "Asymptotes", "SemiLatusRectum"}$

Out[5]=

Use the resource function InteractiveConicPlot to visualize the results of ConicProperties:

In[6]:=

$ResourceFunction["InteractiveConicPlot"][1 + x^2 == y^2, {x, y}]$

Out[7]=

Possible Issues (4)

Each property has specific syntax that is expected. If incorrect data is given, a conic section may not be found:

In[8]:=

Out[8]=

ConicProperties may not be able to resolve some properties into a unique conic section unless you specify additional properties:

In[9]:=

Out[9]=

Adding additional information specifies a unique conic section:

In[10]:=

Out[10]=

Specifying the type of conic you are looking for can sometimes help to return some properties, but may still be insufficient to uniquely determine a full conic section. In this case, ConicProperties will return the properties found:

In[11]:=