Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine how many shuffles restore the list of specified size to its original order
ResourceFunction["ShuffleOrder"][shuffle,n] gives the shuffle order for a size-n list. |
| "type" | string type, as defined in the resource function Shuffle |
| ResourceFunction["Shuffle"][…] | operator form of ResourceFunction["Shuffle"] |
| fun | a pure function that acts on a list |
The shuffle order of a perfect out shuffle of a list of the specified size:
| In[1]:= |
|
| Out[1]= |
|
Same as:
| In[2]:= |
|
| Out[2]= |
|
ShuffleOrder is determined by the PermutationOrder of a shuffle:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
Or, alternatively, by the least common multiple of the lengths of its cycles:
| In[5]:= |
|
| Out[5]= |
|
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
|
The shuffle order can also be determined, possibly less efficiently, using its definition:
| In[8]:= |
![ShuffleOrder2[type_String, n_] := Module[{list = Range[n], order = 0}, NestWhile[ResourceFunction["Shuffle"][type], ResourceFunction["Shuffle"][list, type], (order++; # =!= list) &]; order]](https://www.wolframcloud.com/obj/resourcesystem/images/247/247a2732-bd80-4aa7-8a69-aa9a31d003f6/27ae875189c41146.png)
|
For a milk shuffle:
| In[9]:= |
|
| Out[9]= |
|
| In[10]:= |
|
| Out[10]= |
|
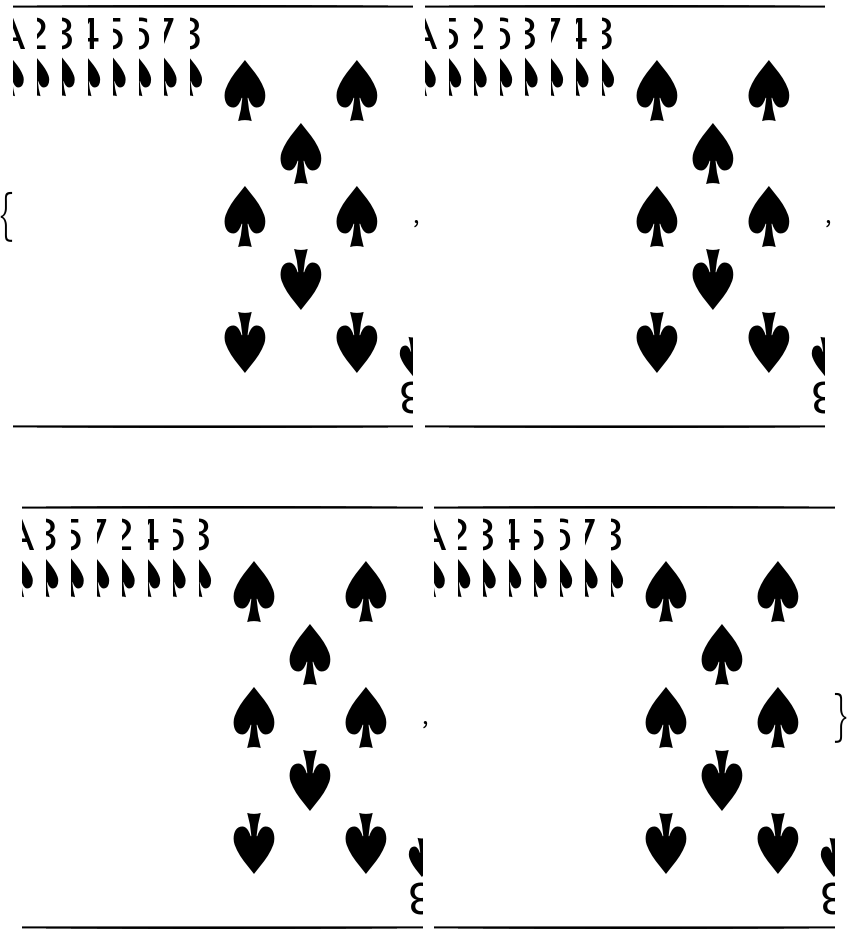
Restore a shuffled deck of cards to its original order:
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License