Applications (4)
Use SolutionRulesToFunctions with the results of DSolve:
Verify the solution:
Solve an initial value problem for an inhomogeneous linear hyperbolic system with constant coefficients:
Use SolutionRulesToFunctions on the solution:
Verify the solutions:
Use SolutionRulesToFunctions with an initial value problem for the heat equation:
Verify the solution:
Use SolutionRulesToFunctions on the Euler-Lagrange equations for a rolling wheel on an inclined plane. In this problem, the translational coordinate y and rotational coordinate θ are assumed to be independent, and constraints are used to determine the Lagrange multiplier for obtaining the equations of motion in terms of the independent coordinates.
The equation of motion for the translational coordinate and its initial conditions:
The solution for equation of motion using DSolve:
Apply SolutionRulesToFunctions:
Verify the solution:
Use the resource function SymbolToSubscript to format some parts of the solution as subscripts:
The equation of motion for the rotational coordinate and its initial conditions:
The solution for this equation of motion using DSolve:
Verify the solution:
Use SymbolToSubscript to format some parts of the solution as subscripts:
![pdes = {D[u[x, t], t] == D[v[x, t], x] + 1, D[v[x, t], t] == -D[u[x, t], x] - 1};
ic = {u[x, 0] == Cos[x]^2, v[x, 0] == Sin[x]};
DSolve[{pdes, ic}, {u[x, t], v[x, t]}, {x, t}] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/2b79f1e3fa90d306.png)
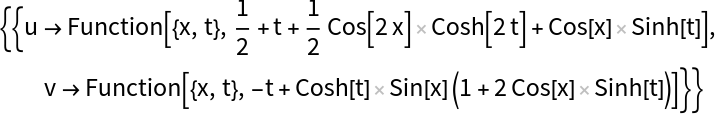
![heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];
hic = u[x, 0] == E^(-x^2);
DSolve[{heqn, hic }, u[x, t], {x, t}]](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/6b8c81041e7a6024.png)
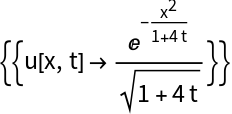
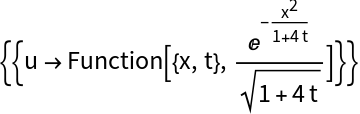
![eqny = {2/3 m g Sin[\[Alpha]] - m y''[t] == 0};
icvy = {y[0] == y0, y'[0] == v0};](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/2370fa3cf60b8124.png)
![ResourceFunction["SymbolToSubscript"][
ResourceFunction[
"SolutionRulesToFunctions", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Simplify@DSolve[Join[eqny, icvy], y[t], t]]]](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/6fc96bf327c2c2d8.png)
![eqn\[Theta] = {1/3 m R g Sin[\[Alpha]] - 1/2 m R^2 \[Theta]''[t] == 0};
icv\[Theta] = {\[Theta][0] == \[Theta]0, \[Theta]'[0] == \[Omega]0};](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/4b14df65eeccc60d.png)
![ResourceFunction["SymbolToSubscript"][
ResourceFunction[
"SolutionRulesToFunctions", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][
Simplify@DSolve[Join[eqn\[Theta], icv\[Theta]], \[Theta][t], t]]]](https://www.wolframcloud.com/obj/resourcesystem/images/1a2/1a263288-a34b-45d8-9883-4278af564273/48255864892fb7b8.png)