Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the irreducible group representation of SU(2) for a given angular momentum
ResourceFunction["WignerMatrix"][j,a] computes the Wigner matrix corresponding to the matrix a representing the irreducible Lie group representation corresponding to angular momentum j. |
For j=1/2, WignerMatrix yields the fundamental representation (i.e. the identity function):
| In[1]:= |
| Out[1]= |
The matrix entries are homogeneous polynomial functions of the elements of the argument matrix ![]() :
:
| In[2]:= |
| Out[2]= | 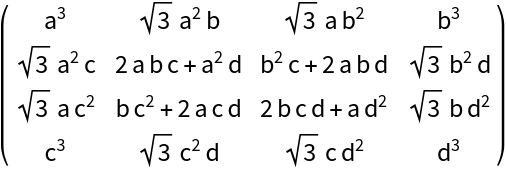 |
Obtain the images of the infinitesimal generators using PauliMatrix:
| In[3]:= | ![jtest = 3/2;
MatrixForm[
Subscript[L, 1] = -(I/2) D[
ResourceFunction["WignerMatrix"][jtest, IdentityMatrix[2] + t I PauliMatrix[1]], t] /. t -> 0]](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/3ce6d1a8a854f732.png) |
| Out[3]= |  |
| In[4]:= |
| Out[4]= | 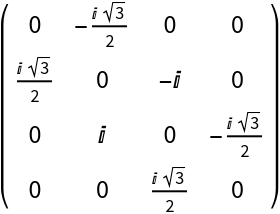 |
| In[5]:= |
| Out[5]= | 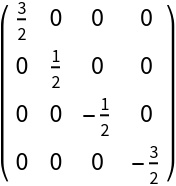 |
Verify an identity:
| In[6]:= |
| Out[6]= |
For j=1 and argument matrices expressed in terms of Euler angles, the result of WignerMatrix is related to EulerMatrix through a similarity transformation:
| In[7]:= | ![arg = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{
SuperscriptBox["E",
RowBox[{"-",
FractionBox[
RowBox[{"I", " ",
RowBox[{"(",
RowBox[{"\[Alpha]", "+", "\[Gamma]"}], ")"}]}], "2"]}]], " ",
RowBox[{"Cos", "[",
FractionBox["\[Beta]", "2"], "]"}]}],
RowBox[{
RowBox[{"-",
SuperscriptBox["E",
RowBox[{"-",
FractionBox[
RowBox[{"I", " ",
RowBox[{"(",
RowBox[{"\[Alpha]", "-", "\[Gamma]"}], ")"}]}], "2"]}]]}], " ",
RowBox[{"Sin", "[",
FractionBox["\[Beta]", "2"], "]"}]}]},
{
RowBox[{
SuperscriptBox["E",
FractionBox[
RowBox[{"I", " ",
RowBox[{"(",
RowBox[{"\[Alpha]", "-", "\[Gamma]"}], ")"}]}], "2"]], " ",
RowBox[{"Sin", "[",
FractionBox["\[Beta]", "2"], "]"}]}],
RowBox[{
SuperscriptBox["E",
FractionBox[
RowBox[{"I", " ",
RowBox[{"(",
RowBox[{"\[Alpha]", "+", "\[Gamma]"}], ")"}]}], "2"]], " ",
RowBox[{"Cos", "[",
FractionBox["\[Beta]", "2"], "]"}]}]}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\); trf = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
RowBox[{"-",
FractionBox["1",
SqrtBox["2"]]}],
FractionBox["I",
SqrtBox["2"]], "0"},
{"0", "0", "1"},
{
FractionBox["1",
SqrtBox["2"]],
FractionBox["I",
SqrtBox["2"]], "0"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\);
ResourceFunction["WignerMatrix"][1, arg] == trf . EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}] . ConjugateTranspose[trf] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/4d8a8ead6d38cdc7.png) |
| Out[7]= |
For general angular momentum j, the entries of WignerMatrix are given by WignerD functions:
| In[8]:= | ![jtest = 3/2;
ResourceFunction["WignerMatrix"][jtest, arg] == Array[WignerD[{jtest, #1 - jtest - 1, #2 - jtest - 1}, \[Alpha], \[Beta], \[Gamma]] &, {2 jtest + 1, 2 jtest + 1}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/19da7b748cac4db7.png) |
| Out[8]= |
Check the multiplicative property of WignerMatrix:
| In[9]:= | ![jtest = 3/2;
Simplify[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)] . ResourceFunction["WignerMatrix"][jtest, ({
{u, v},
{w, x}
})] == ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\) . \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"u", "v"},
{"w", "x"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]]](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/2cf45c1080e317d0.png) |
| Out[9]= |
The determinant of WignerMatrix with angular momentum j is the j(2j+1)th power of the determinant of the argument matrix:
| In[10]:= | ![jtest = 3/2;
Simplify[Det[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]] == Det[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]^(jtest (2 jtest + 1))]](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/4eabcd399157f35f.png) |
| Out[10]= |
The character of the representation, i.e. the trace of WignerMatrix, is given by Tr[WignerMatrix[j,x]]=Det[x]jChebyshevU[2j,Tr[x]/(2Sqrt[Det[x]])]:
| In[11]:= | ![jtest = 3/2; Simplify[Tr[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]] == Det[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]^jtest ChebyshevU[2 jtest, 1/2 Tr[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]/Sqrt[Det[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/0a5dff04a442bdb5.png) |
| Out[11]= |
As a matrix with homogeneous polynomial entries, WignerMatrix must satisfy Euler's homogeneity relation:
| In[12]:= | ![jtest = 3/2; Simplify[
a D[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)], a] + b D[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)], b] + c D[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)], c] + d D[ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)], d] == 2 jtest ResourceFunction["WignerMatrix"][jtest, \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"a", "b"},
{"c", "d"}
},
GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}},
GridBoxSpacings->{"Columns" -> {
Offset[
0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]]](https://www.wolframcloud.com/obj/resourcesystem/images/109/1096e84a-eb9d-47ec-b6bd-1921a27e5a27/06e14ea663d552c5.png) |
| Out[12]= |
This work is licensed under a Creative Commons Attribution 4.0 International License