Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Logit

Source Notebook

The logit function from probability

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["Logit"][p]

computes the logit of p.

Details

The logit function is defined via ResourceFunction["Logit"][x]=Log[x/(1-x)]. It has a zero at x=1/2, is negative for x between 0 and 1/2, and is positive for x between 1/2 and 1. It is odd about x=1/2. For real numbers x outside the range 0<x<1, ResourceFunction["Logit"][x] gives a complex result.
ResourceFunction["Logit"] is a mathematical function, suitable for both symbolic and numerical manipulation.
ResourceFunction["Logit"] gives exact results when possible.
ResourceFunction["Logit"] can be evaluated to arbitrary numerical precision.
ResourceFunction["Logit"] automatically threads over lists.
The logit function is also called log-odds function and is the inverse of the sigmoidal logistic function.

Examples

Basic Examples (3) 

Compute the logit of an exact number:

In[1]:=
ResourceFunction["Logit"][8/10]
Out[1]=

Plot the logit function on the real line:

In[2]:=
Plot[ResourceFunction["Logit"][x], {x, -1.5, 1.5}]
Out[2]=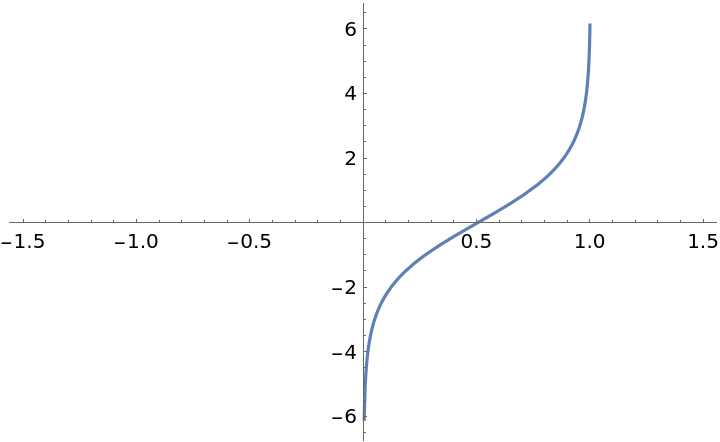

Compute the logit of an approximate number:

In[3]:=
ResourceFunction["Logit"][0.345]
Out[3]=

Logit[x] has a zero at x=1/2:

In[4]:=
ResourceFunction["Logit"][1/2]
Out[4]=

Scope (2) 

Apply Logit to symbolic input:

In[5]:=
ResourceFunction["Logit"][a]
Out[5]=

Logit automatically threads over lists:

In[6]:=
ResourceFunction["Logit"][{8/10, Pi/4}]
Out[6]=

Properties and Relations (3) 

Applying Logit to a real number x outside the range 0<x<1 gives a complex result:

In[7]:=
ResourceFunction["Logit"][-Pi]
Out[7]=

Logit[x] evaluates to -∞ for x=0:

In[8]:=
ResourceFunction["Logit"][0]
Out[8]=

Logit[x] evaluates to ∞ for x=1:

In[9]:=
ResourceFunction["Logit"][1]
Out[9]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 3.0.1 – 27 March 2023
  • 3.0.0 – 24 January 2020
  • 2.0.0 – 06 September 2019
  • 1.0.0 – 26 August 2019

Related Resources

License Information