Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RatioSimplify

Source Notebook

Simplify a list as if it were a ratio

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["RatioSimplify"][list]

returns a simplification of list as a ratio in terms of integers, symbols and symbolic numbers.

ResourceFunction["RatioSimplify"][list,type]

returns the simplification of list as a ratio of the type type.

Details and Options

ResourceFunction["RatioSimplify"] has the attribute HoldFirst.
ResourceFunction["RatioSimplify"] attempts to convert Real valued inputs to symbolic and Integer numbers.
Input type can be any of "SumNormalizedToOne", "EntriesNormalizedToOne", "PieChart", "LowestTerms" or All.
ResourceFunction["RatioSimplify"][list, All] returns an Association of all properties.
The argument type defaults to "LowestTerms".

Examples

Basic Examples (3) 

Simplify a basic ratio:

In[1]:=
ResourceFunction["RatioSimplify"][{2, 4}]
Out[1]=

Simplify a list with more elements according to the elements’ ratios:

In[2]:=
ResourceFunction["RatioSimplify"][{2/3, 5, 15}]
Out[2]=

Return all ratio simplification types as well as a PieChart visualizing the ratio:

In[3]:=
ResourceFunction["RatioSimplify"][{2, 4, 8}, All]
Out[3]=

Scope (3) 

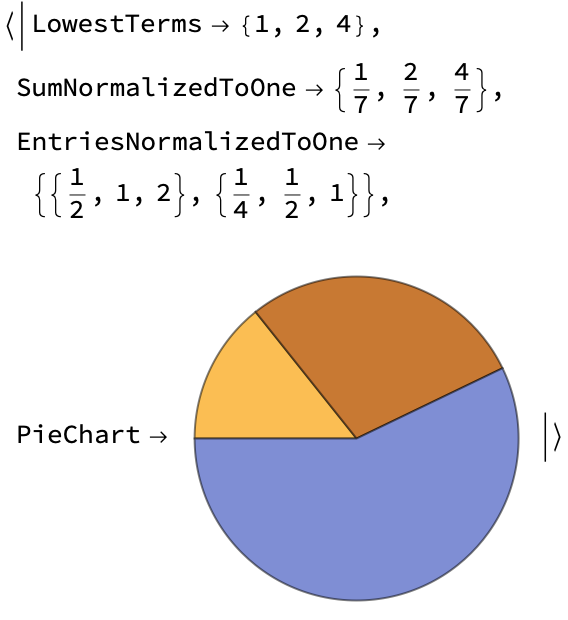Simplify a ratio that combines real-valued and exact-valued inputs:

In[4]:=
ResourceFunction["RatioSimplify"][{2.5 Pi, 4 Sqrt[3] , 8 Pi}]
Out[4]=

Return the ratio with the sum of the entries normalized to 1:

In[5]:=
ResourceFunction[ "RatioSimplify"][{2.5 Pi, 4 Sqrt[3] , 8 Pi}, "SumNormalizedToOne"]
Out[5]=
In[6]:=
Simplify@Total[%]
Out[6]=

RatioSimplify works with symbolic inputs as well as numeric:

In[7]:=
ResourceFunction["RatioSimplify"][{2 Pi^2, .5 Pi}]
Out[7]=
In[8]:=
ResourceFunction["RatioSimplify"][{2 a^2, .5 a}]
Out[8]=

Possible Issues (2) 

RatioSimplify returns unevaluated if it is unable to produce the specified result type:

In[9]:=
ResourceFunction[ "RatioSimplify"][{1/x, 2 x, 3 x}, "SumNormalizedToOne"]
Out[9]=

Because RatioSimplify has the HoldFirst attribute, it may not evaluate to an expected result:

In[10]:=
x = {2, 4, 6}; ResourceFunction["RatioSimplify"][x]
Out[11]=

In cases such as this, Evaluate can be used:

In[12]:=
ResourceFunction["RatioSimplify"][Evaluate[x]]
Out[12]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 01 May 2020

Related Resources

License Information