Details and Options
A Szeged matrix S is a matrix whose entries S〚i,j〛 depend on the number of vertices that are closer to vertex νi or vertex νj of the given graph.
ResourceFunction["SzegedMatrix"] assumes that the graph g is undirected and connected.
ResourceFunction["SzegedMatrix"][g] is equivalent to ResourceFunction["SzegedMatrix"][g,"Edge"].
ResourceFunction["SzegedMatrix"][g,"Edge"] gives an edge-Szeged matrix (sometimes referred to as "the" Szeged matrix), where the nonzero off-diagonal S〚i,j〛 entries correspond to edges connecting vertex νi and vertex νj in the graph.
ResourceFunction["SzegedMatrix"][g,"Path"] gives an path-Szeged matrix, where the off-diagonal S〚i,j〛 entries correspond to paths connecting vertex νi and vertex νj in the graph.
The diagonal entries of a Szeged matrix are taken to be 0.
ResourceFunction["SzegedMatrix"][g,"Edge"] gives a
SparseArray object.
With the option setting
"Symmetric"→False,
ResourceFunction["SzegedMatrix"] gives an unsymmetric matrix whose entries
S〚i,j〛 count the number of vertices that are closer to vertex
νi than to vertex
νj. Vertices equidistant from the two are not counted.
With the default option setting
"Symmetric"→True,
ResourceFunction["SzegedMatrix"] produces a symmetric matrix equivalent to the Hadamard product of an unsymmetric Szeged matrix with its transpose.
ResourceFunction["SzegedMatrix"][mol,"type"] computes the Szeged matrix of a molecule
mol, where the hydrogens are ignored by default. Use the option setting
IncludeHydrogens→All to account for hydrogens.
ResourceFunction["SzegedMatrix"][entity,"type"] computes the Szeged matrix of an entity of type
"Chemical" or
"Graph".

![ResourceFunction["SzegedMatrix"][
Molecule[{"C", "C", "C", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 7}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{7, 3}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{1, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{2, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{7, 18}, "Single"],
Bond[{7, 19}, "Single"]}, {}]]](https://www.wolframcloud.com/obj/resourcesystem/images/02f/02f314c9-fa18-47a2-8a63-dcae626481bb/5f016797877ce898.png)
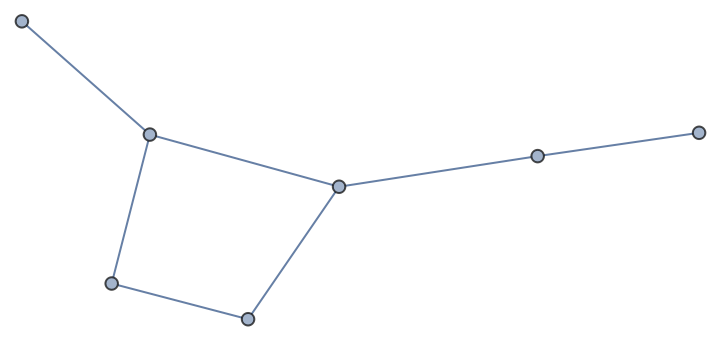
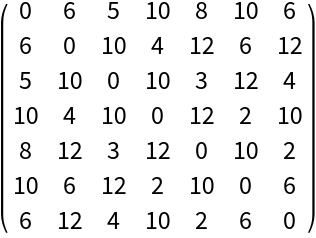
![MatrixForm /@ {ResourceFunction["SzegedMatrix"][g, "Edge", "Symmetric" -> True], ResourceFunction["SzegedMatrix"][g, "Edge", "Symmetric" -> False]}](https://www.wolframcloud.com/obj/resourcesystem/images/02f/02f314c9-fa18-47a2-8a63-dcae626481bb/7ee4f117929b0c24.png)

![MatrixForm /@ {ResourceFunction["SzegedMatrix"][g, "Path", "Symmetric" -> True], ResourceFunction["SzegedMatrix"][g, "Path", "Symmetric" -> False]}](https://www.wolframcloud.com/obj/resourcesystem/images/02f/02f314c9-fa18-47a2-8a63-dcae626481bb/783f2ee007279ed1.png)

![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null, {{1, 2}, {2, 3}, {3, 4}, {3, 5}, {5, 6}, {5, 7}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{0., 0.}, {0., 0.8401680504168059}, {
0.8401680504168059, 1.6803361008336117`}, {
0.8401680504168059, 0.8401680504168059}, {
1.6803361008336117`, 0.8401680504168059}, {
1.260252075625209, 0.}, {2.100420126042015, 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[{{1, 2}, {2, 3}, {3, 4}, {3, 5}, {5, 6}, {5, 7}},
0.023421087284658304`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.023421087284658304], DiskBox[2, 0.023421087284658304], DiskBox[3, 0.023421087284658304], DiskBox[4, 0.023421087284658304], DiskBox[5, 0.023421087284658304], DiskBox[6, 0.023421087284658304], DiskBox[7, 0.023421087284658304]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\);
ResourceFunction["SzegedMatrix"][g, "Edge"] == ResourceFunction["SzegedMatrix"][g, "Path"]*AdjacencyMatrix[g]](https://www.wolframcloud.com/obj/resourcesystem/images/02f/02f314c9-fa18-47a2-8a63-dcae626481bb/50f85114f2134f20.png)
![um = ResourceFunction["SzegedMatrix"][g, "Edge", "Symmetric" -> False];
sm = ResourceFunction["SzegedMatrix"][g, "Edge", "Symmetric" -> True];
sm == um*Transpose[um]](https://www.wolframcloud.com/obj/resourcesystem/images/02f/02f314c9-fa18-47a2-8a63-dcae626481bb/4314a45db89c00e1.png)