Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Inellipse

Source Notebook

Generate the general inellipse of a 2D triangle with specified contact points

Contributed by: Shenghui Yang

ResourceFunction["Inellipse"][{p1,p2,p3},s,t]

returns a 2D Ellipsoid representing the general inellipse of the triangle defined by vertices p1,p2, and p3 given the location s of contact point on segment {p1,p2} and t on {p1,p3}.

ResourceFunction["Inellipse"][{p1,p2,p3},s,t,prop]

gives the value of the specified property.

Details

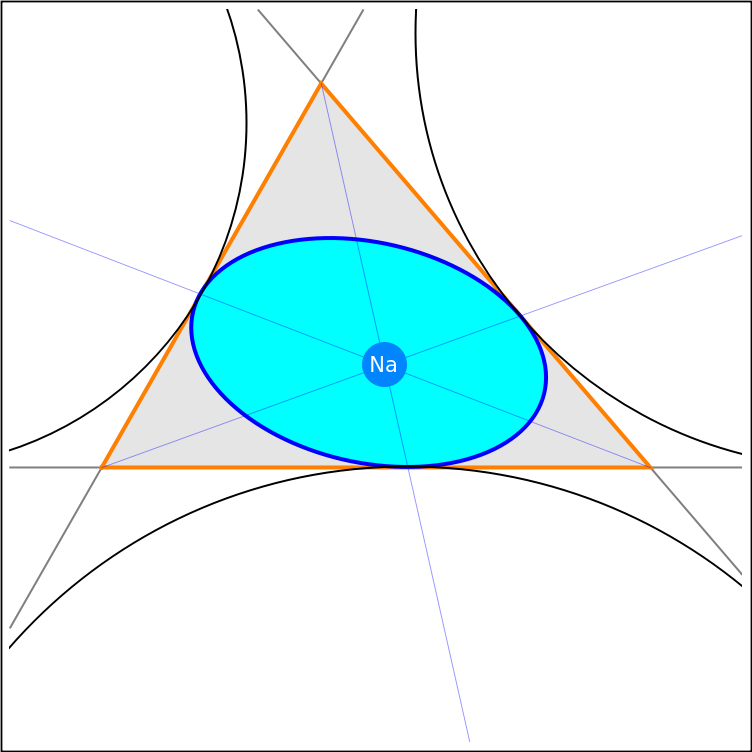
The Steiner inellipse of a triangle is an ellipse inscribed in a triangle with contact points at the midpoints, s=t=1/2. A general inellipse can have different contact points.
The affine location s of the contact point on p1p2 is s·(p2-p1)+p1 and t on p1p3 is t·(p3-p1)+p1.
The following properties are supported:
"Ellipsoid"Ellipsoid representing the inellipse
"Parametric"parametric equation for the inellipse as a pure function
"Implicit"implicit Cartesian equation for the inellipse as a pure function
"All"returns addtional entries to ResourceFunction["EllipseProperties"]
The additional entries included in the full property list include:
"ContactPoints"three contact points on the reference triangle
"ConjugateHalfDiameterVectors"two vectors construct the "Parametric" form
"BrianchonPoint"the concurrence of three lines joining triangle vertices and contacts
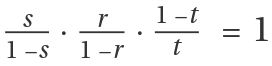
Due to the concurrency at the Brianchon point, by Ceva's theorem, , where s,t and r are the affine location of the three contact points on each side. See "Properties and Relations" for choice of convention following the definition of argument in this function.
ResourceFunction["Inellipse"][{p1,p2,p3},s,t,prop] is equivalent to ResourceFunction["Inellipse"][Triangle[{p1,p2,p3}],s,t,prop]

Examples

Basic Examples (2) 

Create the Steiner inellipse (tangent to midpoints) for a given triangle:

In[1]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 1.8}}; iep = ResourceFunction["Inellipse"][triVtx, 0.5, 0.5]
Out[2]=

Show it:

In[3]:=
Graphics[{ {Opacity[0.4], EdgeForm[{Thick, Blue}], Triangle[triVtx]}, {LightBlue, iep}, {Black, PointSize[0.02], Point[Mean[#]] & /@ Subsets[triVtx, {2}]} }]
Out[3]=

Find the Cartesian equation for a given triangle:

In[4]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 1.8}}; iep = ResourceFunction["Inellipse"][triVtx, 0.5, 0.5, "Implicit"]
Out[5]=

Scope (2) 

Find parametric form for an inellipse:

In[6]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 2}};
In[7]:=
iep = ResourceFunction["Inellipse"][triVtx, 0.5, 0.4]; iepFunc = ResourceFunction["Inellipse"][triVtx, 0.5, 0.4, "Parametric"]
Out[8]=

Lay the points from parametric function over the circumference of in-ellipsoid:

In[9]:=
pts = Point@Map[iepFunc, Subdivide[-Pi, Pi, 24]]; Graphics[{ {Opacity[0.4], EdgeForm[{Thick, Blue}], Triangle[triVtx]}, {LightBlue, iep}, {Black, PointSize[0.015], pts} }]
Out[10]=

Find all documented properties of an inellipse:

In[11]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 1.8}}; iepp = ResourceFunction["Inellipse"][triVtx, 0.3, 0.4, "All"]; Dataset[{iepp}]
Out[12]=

Properties and Relations (1) 

Use Ceva's theorem to find the third contact point r:

In[13]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 1.8}}; iep = ResourceFunction["Inellipse"][triVtx, 0.3, 0.4];
In[14]:=
contact3 = NSolveValues[.3/(1 - .3)*r/(1 - r)*(1 - .4)/.4 == 1, r][[1]];
In[15]:=
contacts = MapThread[#1 /. #2 &, { ListConvolve[{{\[Lambda]}, {1 - \[Lambda]}}, Append[triVtx, triVtx[[1]]]], {\[Lambda] -> .3, \[Lambda] -> contact3, \[Lambda] -> 1 - .4}}];
In[16]:=
Graphics[{ {Opacity[0.4], EdgeForm[{Thick, Blue}], Triangle[triVtx]}, {LightBlue, iep}, {Black, PointSize[0.02], Point[contacts]} }]
Out[16]=

Possible Issues (4) 

Inellipse function returns unevaluated for degenerated triangle:

In[17]:=
ResourceFunction["Inellipse"][{{1, 0}, {2, 0}, {3, 0}}, 0.2, 0.3]
Out[17]=

Inellipse function returns unevaluated for degenerated ellipse:

In[18]:=
ResourceFunction["Inellipse"][{{1, 0}, {2, 0}, {3, 3}}, 0, 0.3]
Out[18]=
In[19]:=
ResourceFunction["Inellipse"][{{1, 0}, {2, 0}, {3, 3}}, 1, 1]
Out[19]=

Inellipse function returns unevaluated for symbolic expression:

In[20]:=
ResourceFunction[ "Inellipse"][{{1, 0}, {\[FormalV], 0}, {3, 3}}, 0, 0.3]
Out[20]=
In[21]:=
ResourceFunction[ "Inellipse"][{{1, 0}, {2, 0}, {3, 3}}, .3, \[FormalV]]
Out[21]=

Inellipse function returns unevaluated for unsupported properties:

In[22]:=
ResourceFunction[ "Inellipse"][{{1, 0}, {2, 0}, {3, 3}}, .3, .5, "InvalidProperty"]
Out[22]=

Neat Examples (2) 

Mutually touching inellipses of a triangle:

In[23]:=
triVtx = {{-1, 0}, {2, 0}, {1.7, 2.5}};
In[24]:=
iep = ResourceFunction["Inellipse"][triVtx, 0.4, #, "Implicit"] & /@ Range[0.2, 0.8, 0.1];
In[25]:=
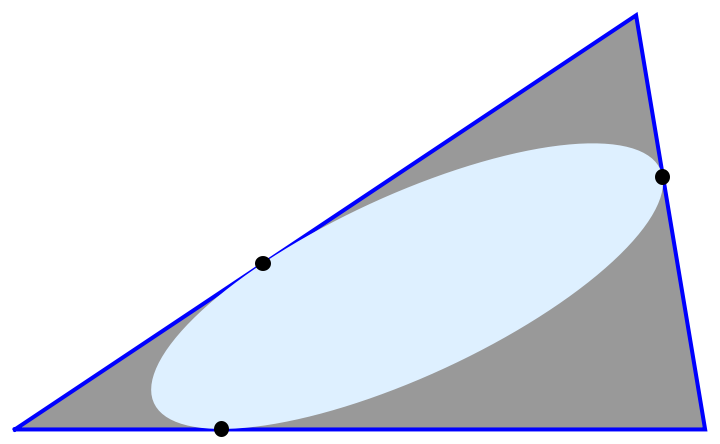
ContourPlot[iep, {\[FormalX], -1, 2}, {\[FormalY], -0.1, 2.5}, Prolog -> {Triangle[triVtx]}, AspectRatio -> 1/1.5, Frame -> False]
Out[25]=

Mandart inellipse and excircles. The Brianchon point K of Mandart inellipse is the Nagel point:

In[26]:=
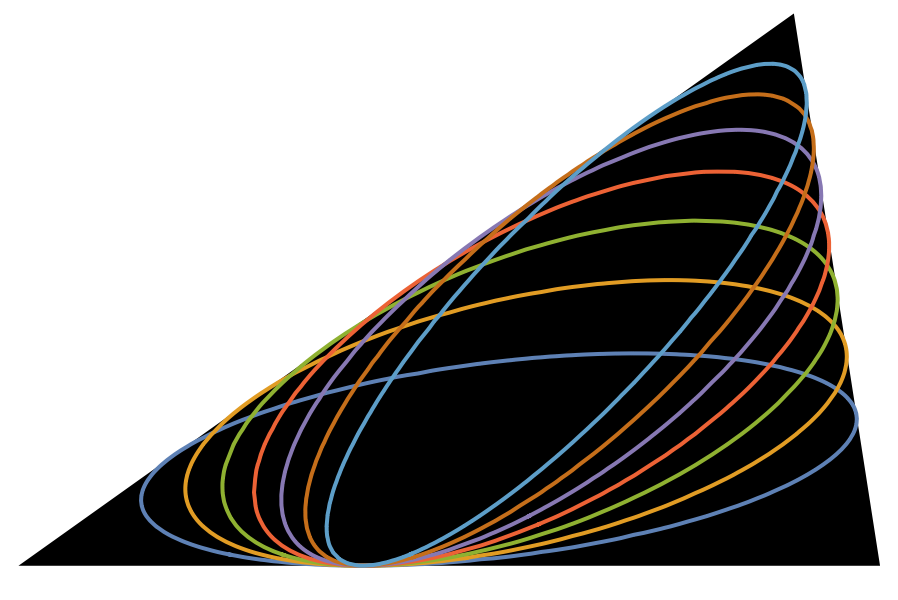
triVtx = {{-1, 0}, {2, 0}, {0.2, 2.1}}; vtxPair = Partition[Append[triVtx, triVtx[[1]]], 2, 1]; sideLen = EuclideanDistance[#1, #2] & @@@ vtxPair; s = (sideLen[[1]] - sideLen[[3]] + sideLen[[2]])/(2*sideLen[[1]]); t = (-sideLen[[1]] + sideLen[[3]] + sideLen[[2]])/(2*sideLen[[3]]);

Compare the coordinate of K and that of Nagel point:

In[27]:=
ResourceFunction["Inellipse"][triVtx, s, t, "All"]["BrianchonPoint"]
Out[27]=
In[28]:=
na = ResourceFunction["NagelPoint"][triVtx]; na[[1]]
Out[29]=

Visualize their positions with Mandart inellipse, the reference triangle and three excircles:

In[30]:=
iep = ResourceFunction["Inellipse"][triVtx, s, t]; Graphics[ {{Gray, InfiniteLine /@ vtxPair}, {EdgeForm[{Thick, Orange}], Opacity[0.1], Triangle[triVtx]}, {EdgeForm[{Thick, Blue}], Cyan, iep}, TriangleConstruct[triVtx, {"Excircle", #}] & /@ triVtx, {Thin, Blue, HalfLine[{triVtx[[#]], na[[1]]}] & /@ {1, 2, 3}}, {PointSize[Scaled[0.06]], Hue[0.58, 1, 1], na, Text[Style["Na", White, FontSize -> Scaled[0.03]], Part[na, 1]]} }, PlotRange -> {{-1.5, 2.5}, {-1.5, 2.5}}] // Framed
Out[31]=

Publisher

Shenghui Yang

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.1 – 25 October 2024
  • 1.0.0 – 23 October 2024

Source Metadata

  • Citation:
    • Imre Juhász: Control point based representation of inellipses of triangles, Annales Mathematicae et Informaticae 40 (2012) pp. 37–46, p.44

Related Resources

Author Notes

This function does not handle degenerated case. To make proper visualization and maintain numeric stability, a hard limit for s and t are imposed: 0.02<=s,t<=0.98.

License Information