Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AbstractCoproduct

Source Notebook

Represent the abstract coproduct of an arbitrary collection of objects in an abstract category

Contributed by: Jonathan Gorard

ResourceFunction["AbstractCoproduct"][ob,coprod,inj,comp,id]

represents the abstract coproduct of the collection of objects ob, with coproduct symbol coprod, injection morphism names inj, composition symbol comp and identity symbol id.

ResourceFunction["AbstractCoproduct"][…,obuniv,morphuniv,morphuniq]

represents an abstract coproduct with a universal property characterized by the universal object obuniv, universal morphisms morphuniv and unique morphism morphuniq.

ResourceFunction["AbstractCoproduct"][assoc]

represents an abstract coproduct using the association of object list, coproduct symbol, injection morphism list, composition symbol, identity symbol, universal object, universal morphism list and unique morphism assoc.

ResourceFunction["AbstractCoproduct"][…][AbstractCategory[…]]

embeds an abstract coproduct into the specified abstract category.

ResourceFunction["AbstractCoproduct"][ResourceFunction["AbstractCoproduct"][…],coprod,comp,id]

makes a new abstract coproduct from an old coproduct by imposing new coproduct symbol coprod, new composition symbol comp and new identity symbol id.

Details and Options

The coproduct of a collection of objects in an abstract category consists of a distinguished object (the coproduct object) together with a family of incoming morphisms to this object (the injection morphisms), one for each element of the collection, in such a way that a certain universal property is satisfied. The universal property essentially indicates that the coproduct object is the most general such object that can exist, by asserting that any other object with injection morphisms from the elements of the collection must also have a unique morphism from the coproduct object.
Abstract coproducts are categorically dual to abstract products.
Abstract coproducts capture many familiar constructions from mathematics such as disjoint unions (in the category of sets or topological spaces), direct sums (in the category of modules or vector spaces), free products (in the category of groups), etc., and generalize them to arbitrary categories.
An abstract coproduct may be characterized formally as a colimit taken over a discrete index category (i.e. an index category in which the only morphisms are identity morphisms on the objects).
An abstract presentation of a coproduct can therefore be given in terms of a collection of objects, a coproduct symbol, a composition symbol, an identity symbol, and a collection of injection morphisms from the objects in the collection to the coproduct object, together with symbols for a universal object, a collection of universal morphisms from the objects in the collection to the universal object, and a unique morphism from the coproduct object to the universal object, in order to characterize the universal property.
ResourceFunction["AbstractCoproduct"] supports the specification of abstract coproducts either by eight lists/symbols (a list of objects ob, a coproduct symbol coprod, a list of injection morphism names inj, a composition symbol comp, an identity symbol id, a universal object symbol obuniv, a list of universal morphism names morphuniv and a unique morphism name morphuniq) or by an explicit association of the form <|"Objects"→ob,"CoproductSymbol"→coprod,"InjectionMorphismNames"→inj,"CompositionSymbol"→comp,"IdentitySymbol"→id,"UniversalObjectName"→obuniv,"UniversalMorphismNames"→morphuniv,"UniqueMorphismName"→morphuniq|>.
Where specified, the coproduct symbol coprod should be an operator of arbitrary arity, the composition symbol comp should be a binary operator and the identity symbol id should be a unary operator.
When specifying an abstract coproduct by a collection of lists/symbols, ResourceFunction["AbstractCoproduct"] allows one to omit the coproduct symbol, the list of injection morphism names, the composition symbol, the identity symbol, the universal object symbol, the list of universal morphism names or the unique morphism name (or certain combinations of the above). When the coproduct symbol, composition symbol or identity symbol is omitted, Times (×), CircleDot (⊙) and OverTilde (∼) are assumed by default. When the list of injection morphisms is omitted, the default naming convention of , ,… is assumed. When the universal object or unique morphism symbols are omitted, Y and f are assumed by default. When the list of universal morphism names is omitted, the default naming convention of f1, f2,… is assumed.
If the function succeeds in constructing the specified abstract coproduct, it will return a ResourceFunction["AbstractCoproduct"] expression.
Objects and morphisms that form part of the defining universal property of the abstract coproduct are indicated using ForAll (∀) and Exists (∃) quantifiers, as appropriate. Unique morphisms are designated using the special-purpose ∃! quantifier, and are indicated in all directed graph representations using dashed (rather than solid) lines.
ResourceFunction["AbstractCoproduct"] expressions can be applied to AbstractCategory expressions in order to embed the corresponding coproduct within the specified category (in such a way that the universal property is satisfied).
In ResourceFunction["AbstractCoproduct"], the following properties are supported:
"Objects"list of objects in the abstract coproduct
"ObjectCount"number of objects in the abstract coproduct
"MorphismAssociation"association of morphisms/edges in the abstract coproduct
"MorphismNames"list of names of morphisms in the abstract coproduct
"MorphismEdges"list of directed edges associated with morphisms in the abstract coproduct
"MorphismCount"number of morphisms in the abstract coproduct
"SimpleMorphismAssociation"association of morphism names/edges in the abstract coproduct with self-loops removed
"SimpleMorphismNames"list of names of morphisms in the abstract coproduct with self-loops removed
"SimpleMorphismEdges"list of directed edges associated with morphisms in the abstract coproduct with self-loops removed
"SimpleMorphismCount"number of morphisms in the abstract coproduct with self-loops removed
"UniversalObjects"list of objects in the abstract coproduct characterizing the universal property
"UniversalObjectCount"number of objects in the abstract coproduct characterizing the universal property
"UniversalMorphismAssociation"association of morphism names/edges in the abstract coproduct characterizing the universal property
"UniversalMorphismNames"list of names of morphisms in the abstract coproduct characterizing the universal property
"UniversalMorphismEdges"list of directed edges associated with morphisms in the abstract coproduct characterizing the universal property
"UniversalMorphismCount"number of morphisms in the abstract coproduct characterizing the universal property
"UniversalReducedMorphismAssociation"association of morphism names/edges the abstract coproduct characterizing the universal property, modulo morphism equivalences
"UniversalReducedMorphismNames"list of names of morphisms in the abstract coproduct characterizing the universal property, modulo morphism equivalences
"UniversalReducedMorphismEdges"list of directed edges associated with morphisms in the abstract coproduct characterizing the universal property, modulo morphism equivalences
"UniversalReducedMorphismCount"number of morphisms in the abstract coproduct characterizing the universal property, modulo morphism equivalences
"UniversalSimpleMorphismAssociation"association of morphism names/edges in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed
"UniversalSimpleMorphismNames"list of names of morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed
"UniversalSimpleMorphismEdges"list of edges associated with morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed
"UniversalSimpleMorphismCount"number of morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed
"UniversalReducedSimpleMorphismAssociation"association of morphism names/edges in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences
"UniversalReducedSimpleMorphismNames"list of names of morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences
"UniversalReducedSimpleMorphismEdges"list of directed edges associated with morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences
"UniversalReducedSimpleMorphismCount"number of morphisms in the abstract coproduct characterizing the universal property, with self-loops and multiedges removed, and modulo morphism equivalences
"CoproductSymbol"symbol used to denote coproducts of objects (should be an operator of arbitrary arity)
"CompositionSymbol"symbol used to denote morphism composition (should be a binary operator)
"IdentitySymbol"symbol used to denote identity morphisms (should be a unary operator)
"CoproductCategory"abstract category with morphisms representing the abstract coproduct
"UniversalCoproductCategory"abstract category with morphisms characterizing the universal property of the abstract coproduct
"UniversalCoproductEquations"list of equations implicitly imposed by the requirement that the universal property of the abstract coproduct is satisfied
"FullLabeledGraph"directed graph form of the abstract coproduct with labels on the morphisms
"FullUnlabeledGraph"directed graph form of the abstract coproduct with no labels on the morphisms
"SimpleLabeledGraph"directed graph form of the abstract coproduct, with self-loops removed, with labels on the morphisms
"SimpleUnlabeledGraph"directed graph form of the abstract coproduct, with self-loops removed, with no labels on the morphisms
"UniversalFullLabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with labels on the morphisms
"UniversalFullUnlabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with no labels on the morphisms
"UniversalReducedLabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, modulo morphism equivalences, with labels on the morphisms
"UniversalReducedUnlabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, modulo morphism equivalences, with no labels on the morphisms
"UniversalSimpleLabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with self-loops and multiedges removed, with labels on the morphisms
"UniversalSimpleUnlabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with self-loops and multiedges removed, with no labels on the morphisms
"UniversalReducedSimpleLabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with self-loops and multiedges removed, modulo morphism equivalences, with labels on the morphisms
"UniversalReducedSimpleUnlabeledGraph"directed graph form characterizing the universal property of the abstract coproduct, with self-loops and multiedges removed, modulo morphism equivalences, with no labels on the morphisms
"AssociationForm"abstract coproduct represented as an association of a list of objects, a coproduct symbol, a list of injection morphism names, a composition symbol, an identity symbol, a universal object name, a list of universal morphism names and a unique morphism name
"Properties"list of properties

Examples

Basic Examples (3) 

Construct a simple abstract coproduct of objects A and B:

In[1]:=
coproduct = ResourceFunction["AbstractCoproduct"][{A, B}]
Out[1]=

Show the full directed graph with labels on the morphisms:

In[2]:=
coproduct["FullLabeledGraph"]
Out[2]=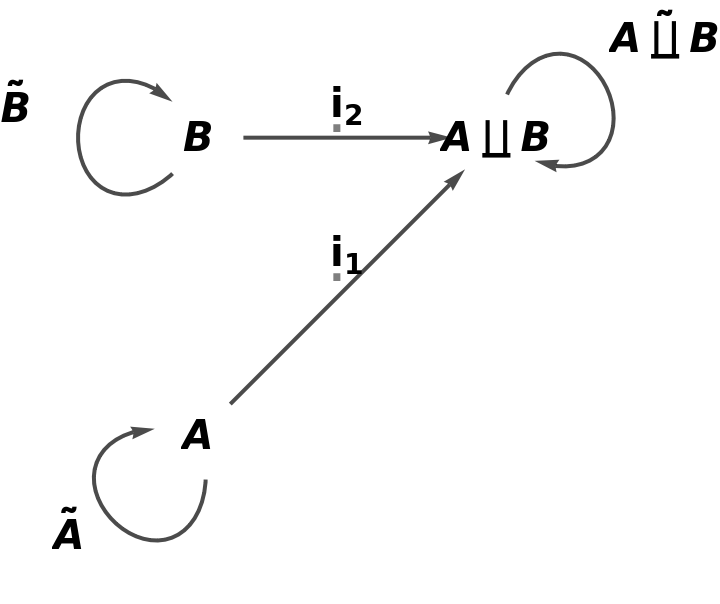

Show the full directed graph without labels on the morphisms:

In[3]:=
coproduct["FullUnlabeledGraph"]
Out[3]=

Show the full directed graph characterizing the universal property, with labels on the morphisms:

In[4]:=
coproduct["UniversalFullLabeledGraph"]
Out[4]=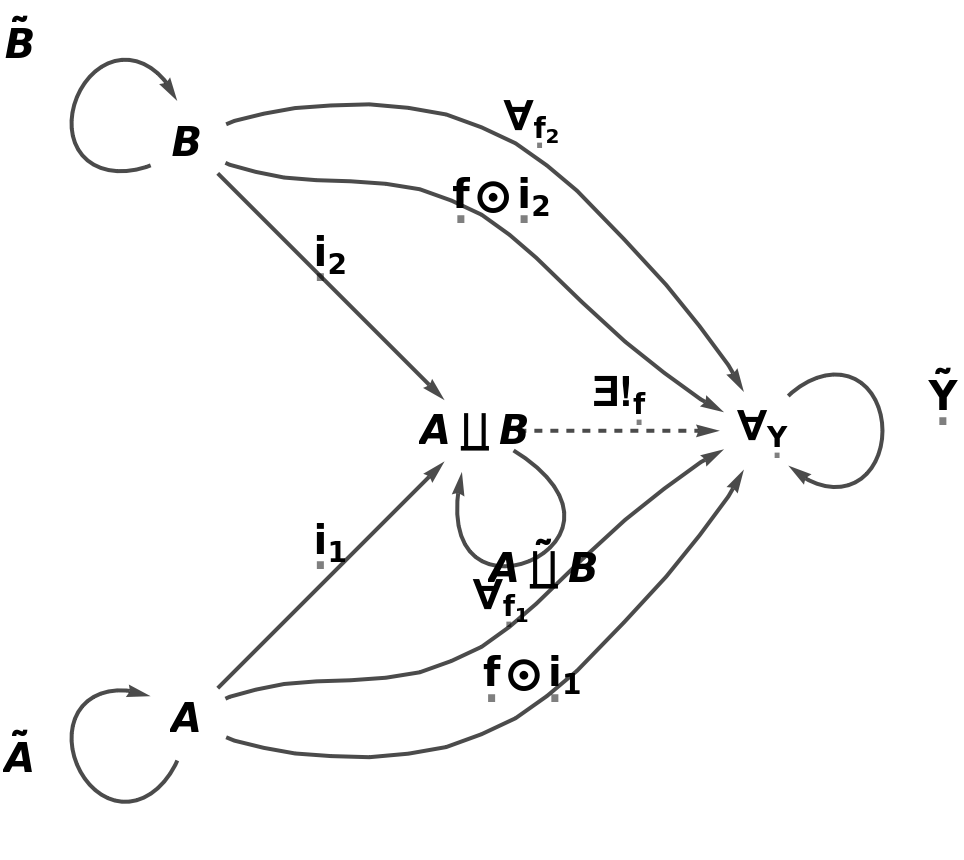

Show the full directed graph characterizing the universal property, without labels on the morphisms:

In[5]:=
coproduct["UniversalFullUnlabeledGraph"]
Out[5]=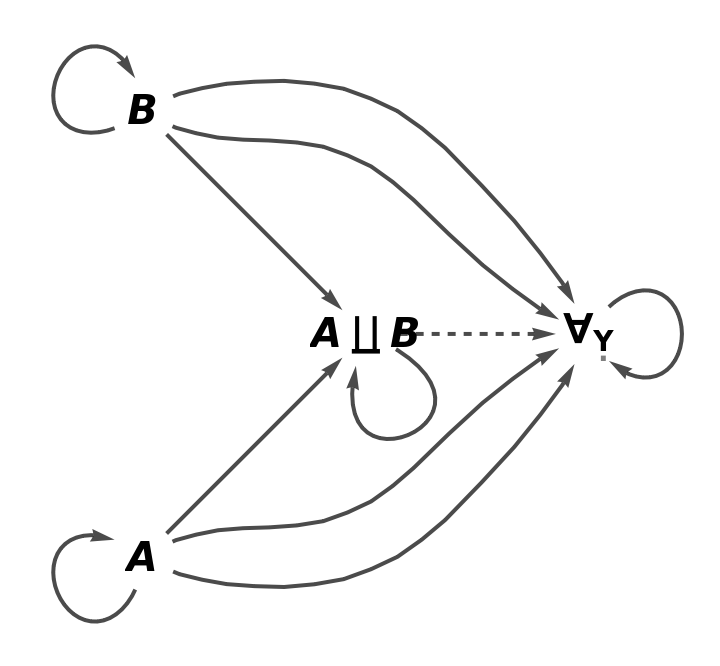

Show the Association of morphisms:

In[6]:=
coproduct["MorphismAssociation"]
Out[6]=

Show the Association of (quantified) morphisms characterizing the universal property:

In[7]:=
coproduct["UniversalMorphismAssociation"]
Out[7]=

Show the list of directed edges characterizing the universal property:

In[8]:=
coproduct["UniversalMorphismEdges"]
Out[8]=

Show the list of (quantified) equations characterizing the universal property:

In[9]:=
coproduct["UniversalCoproductEquations"]
Out[9]=

Construct an abstract coproduct of objects U, V and W, but with coproduct symbol ⊕, injection morphisms j1, j2 and j3, composition and identity symbols ⊗ and ─, and with a universal property characterized by universal object Q, universal morphisms m1, m2 and m3 and unique morphism u:

In[10]:=
coproduct = ResourceFunction["AbstractCoproduct"][{U, V, W}, CirclePlus, {j1, j2, j3}, CircleTimes, OverBar, Q, {m1, m2, m3}]
Out[10]=

Show the full directed graph characterizing the universal property, with labels on the morphisms:

In[11]:=
coproduct["UniversalFullLabeledGraph"]
Out[11]=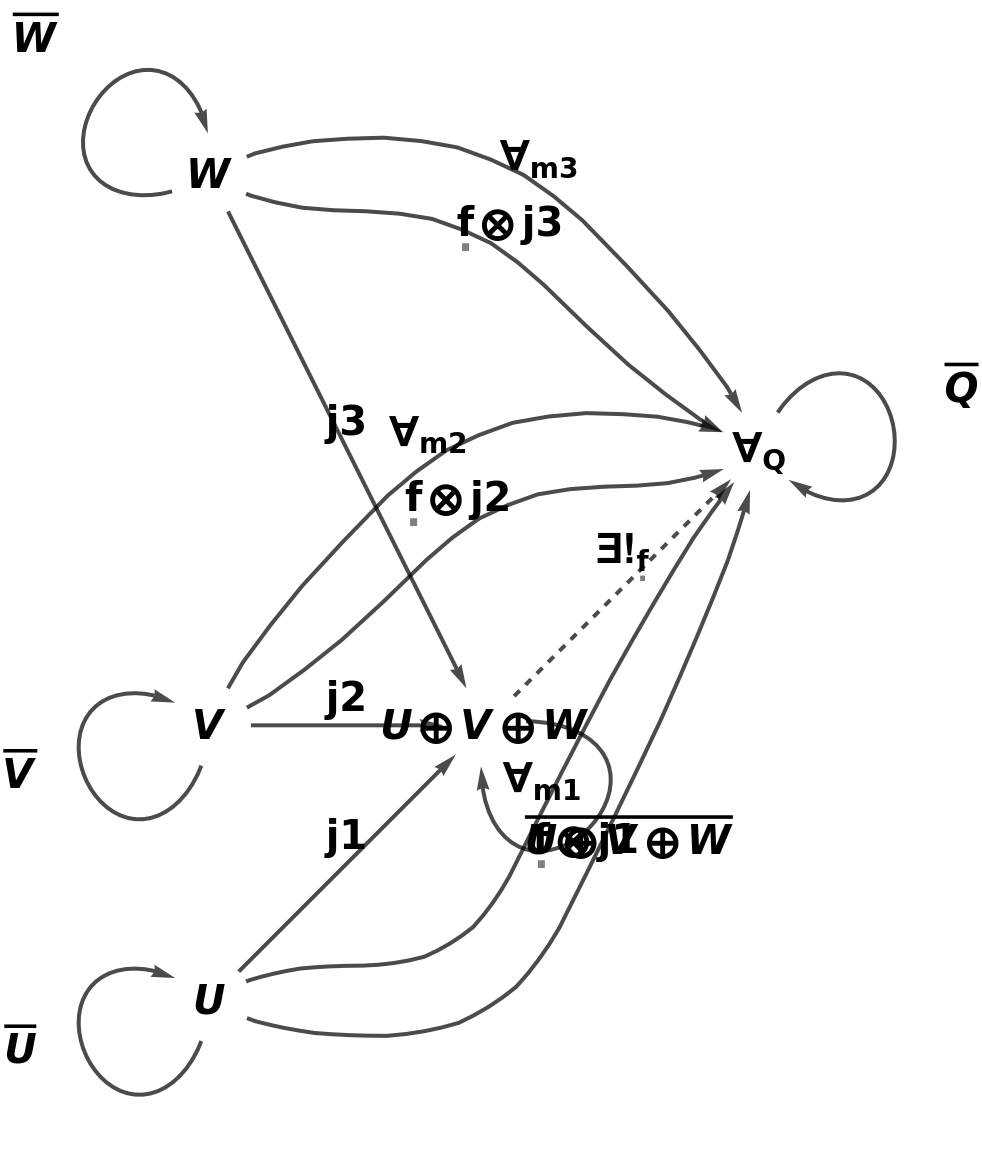

Show the full directed graph characterizing the universal property, without labels on the morphisms:

In[12]:=
coproduct["UniversalFullUnlabeledGraph"]
Out[12]=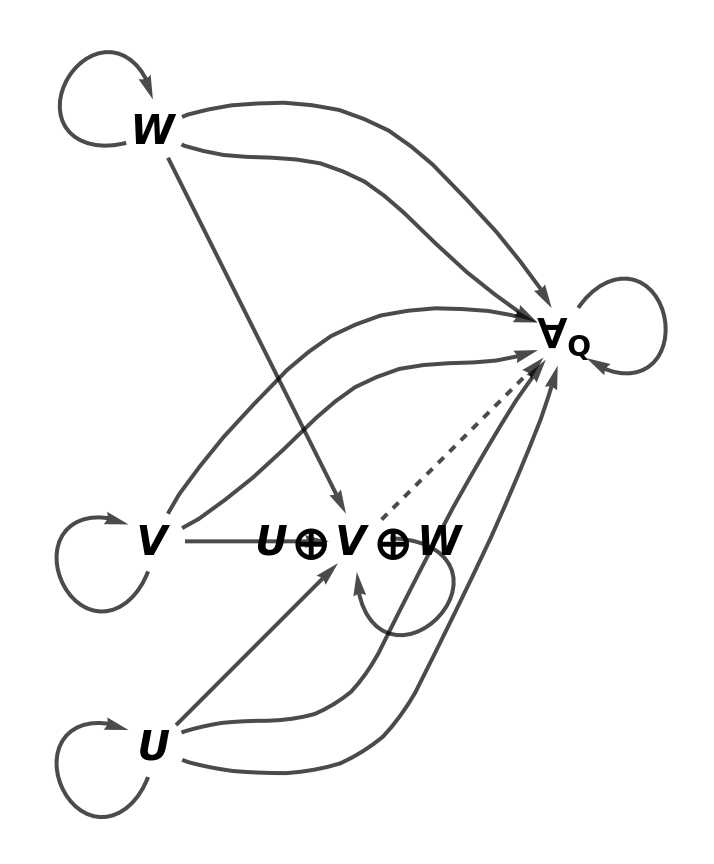

Show the reduced directed graph characterizing the universal property, with all equivalences between morphisms imposed and with labels on the morphisms:

In[13]:=
coproduct["UniversalReducedLabeledGraph"]
Out[13]=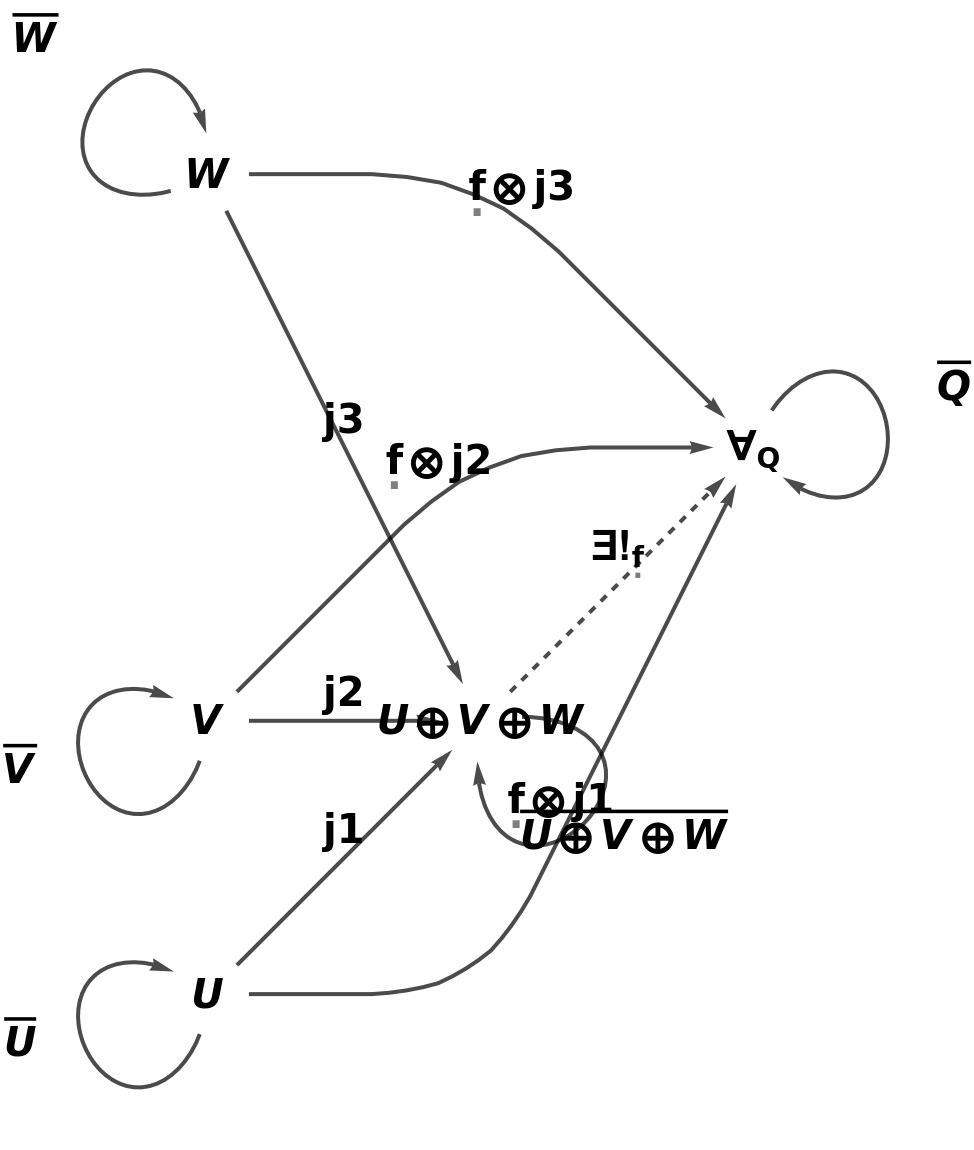

Show the reduced directed graph characterizing the universal property, without labels on the morphisms:

In[14]:=
coproduct["UniversalReducedUnlabeledGraph"]
Out[14]=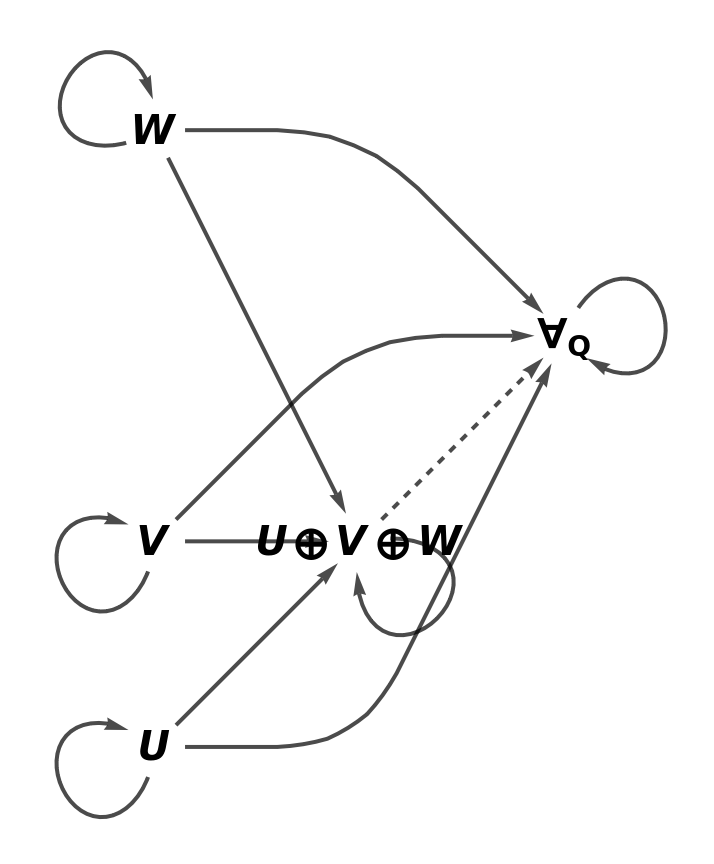

Show the Association of (quantified) morphisms characterizing the universal property, with all equivalences between morphisms imposed:

In[15]:=
coproduct["UniversalReducedMorphismAssociation"]
Out[15]=

Show the list of (quantified) equations characterizing the universal property:

In[16]:=
coproduct["UniversalCoproductEquations"]
Out[16]=

Show the association form of the abstract coproduct:

In[17]:=
coproduct["AssociationForm"]
Out[17]=

Construct an abstract coproduct of objects X and Y:

In[18]:=
coproduct = ResourceFunction["AbstractCoproduct"][{X, Y}]
Out[18]=

Construct an abstract category consisting of morphisms from X and Y to some common object Z:

In[19]:=
category = ResourceFunction["AbstractCategory"][<|f -> {X, Z}, g -> {Y, Z}|>]
Out[19]=

Embed the abstract coproduct into the abstract category (in such a way that the universal property is satisfied):

In[20]:=
newCategory = coproduct[category]
Out[20]=
In[21]:=
newCategory["FullLabeledGraph"]
Out[21]=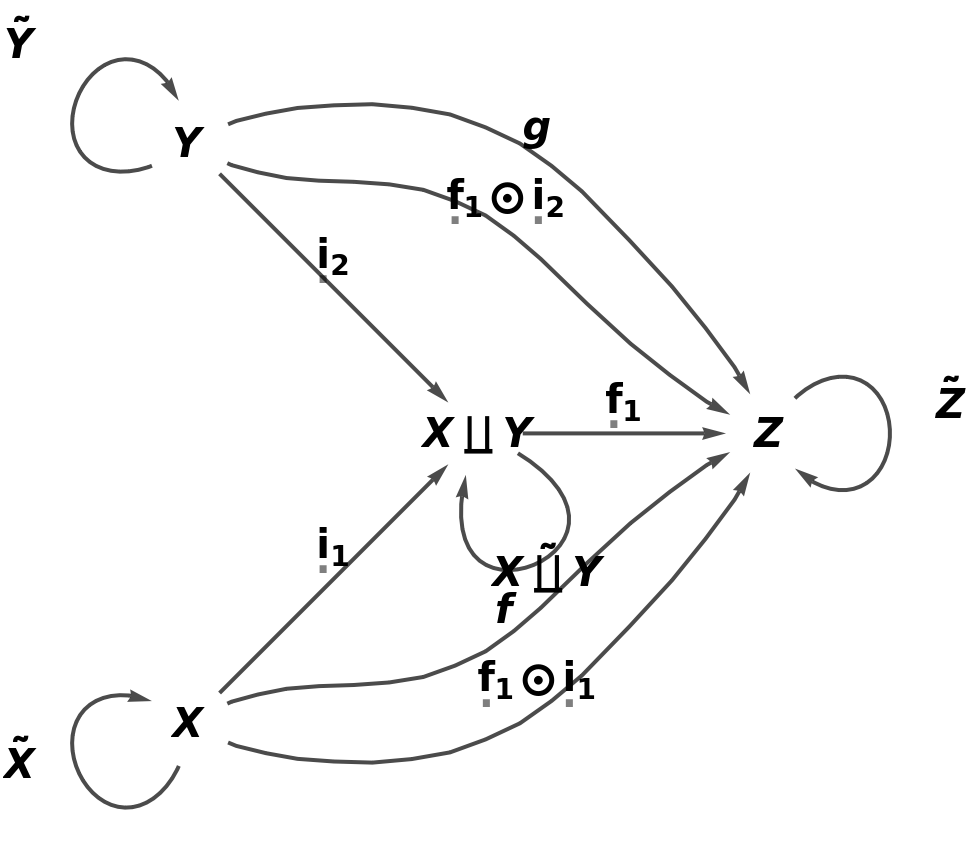

Validate that the universal property is indeed satisfied:

In[22]:=
newCategory["ReducedLabeledGraph"]
Out[22]=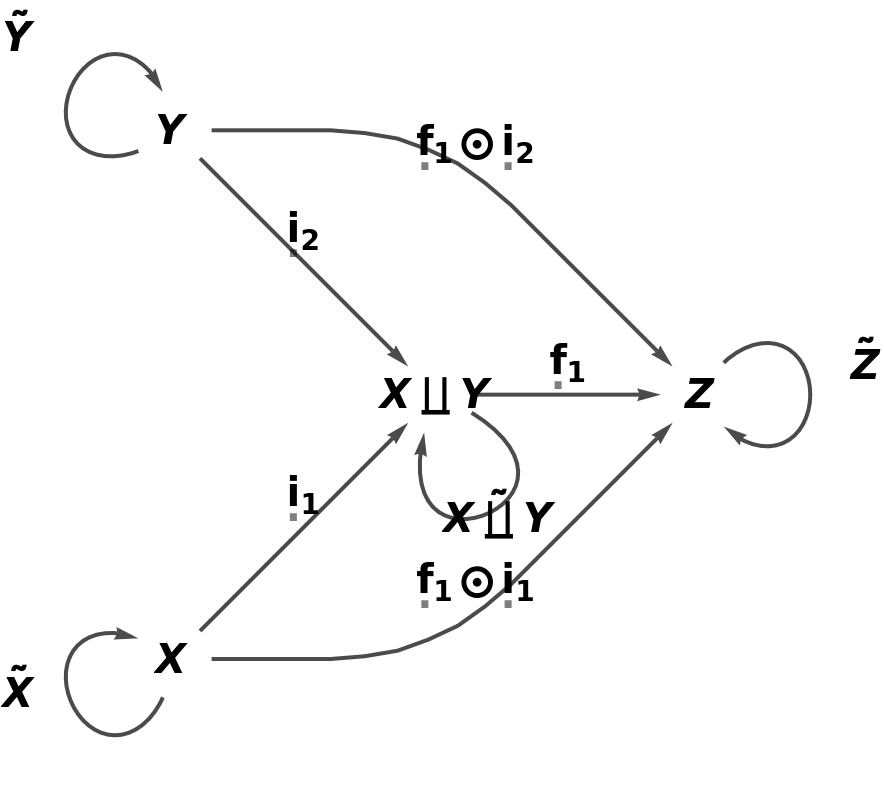
In[23]:=
newCategory["MorphismEquivalences"]
Out[23]=

Construct a more complicated abstract category consisting of additional morphisms from X and Y to a further common object W:

In[24]:=
category2 = ResourceFunction["AbstractCategory"][<|f -> {X, Z}, g -> {Y, Z}, h -> {X, W}, i -> {Y, W}|>]
Out[24]=

Embed the abstract coproduct into the more complicated abstract category and validate that the universal property is still satisfied:

In[25]:=
newCategory2 = coproduct[category2]
Out[25]=
In[26]:=
newCategory2["FullLabeledGraph"]
Out[26]=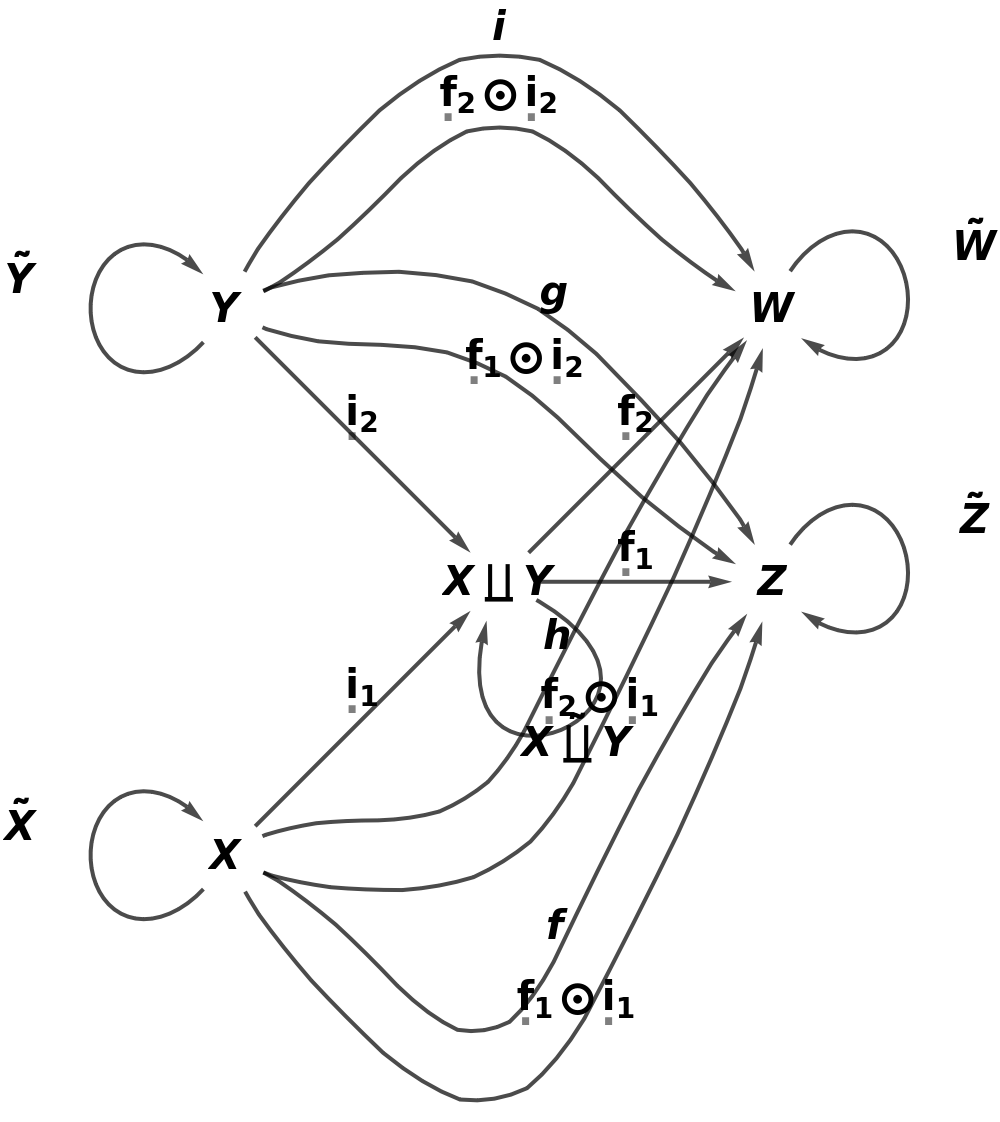
In[27]:=
newCategory2["ReducedLabeledGraph"]
Out[27]=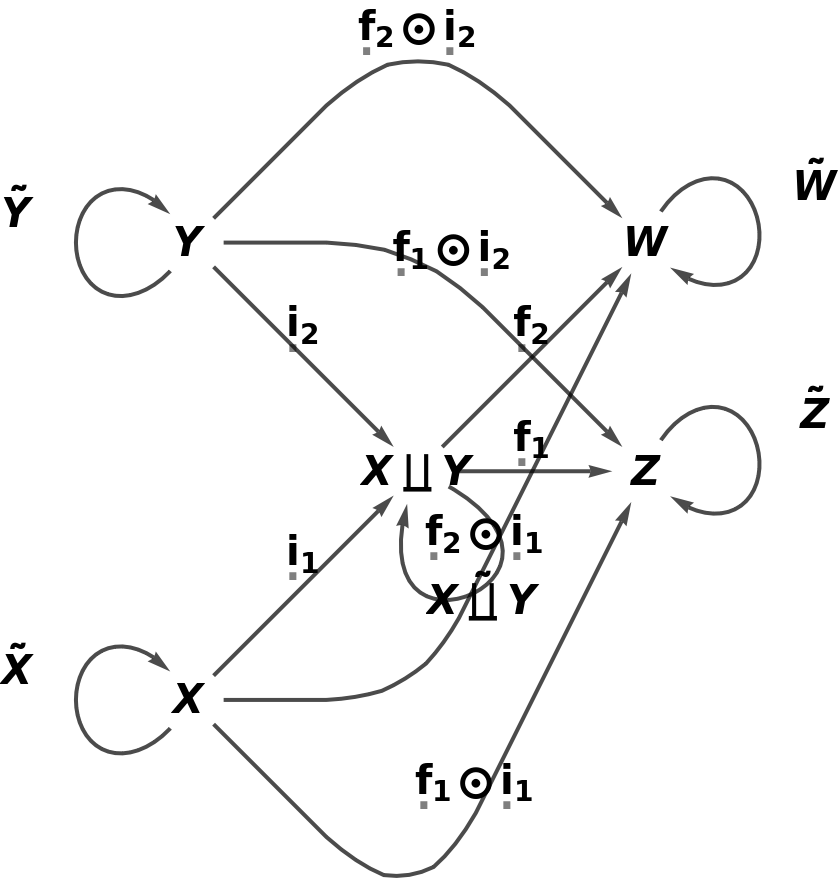
In[28]:=
newCategory2["MorphismEquivalences"]
Out[28]=

Compute minimal abstract category representations of the abstract coproduct and its defining universal property, respectively:

In[29]:=
coproduct["CoproductCategory"]
Out[29]=
In[30]:=
coproduct["UniversalCoproductCategory"]
Out[30]=

Scope (2) 

Abstract coproducts can be constructed from a list of objects, a coproduct symbol, a list of names of injection morphisms, a composition symbol and an identity symbol:

In[31]:=
coproduct = ResourceFunction["AbstractCoproduct"][{X, Y, Z}, CirclePlus, {j1, j2, j3}, CircleTimes, OverBar]
Out[31]=
In[32]:=
coproduct["UniversalFullLabeledGraph"]
Out[32]=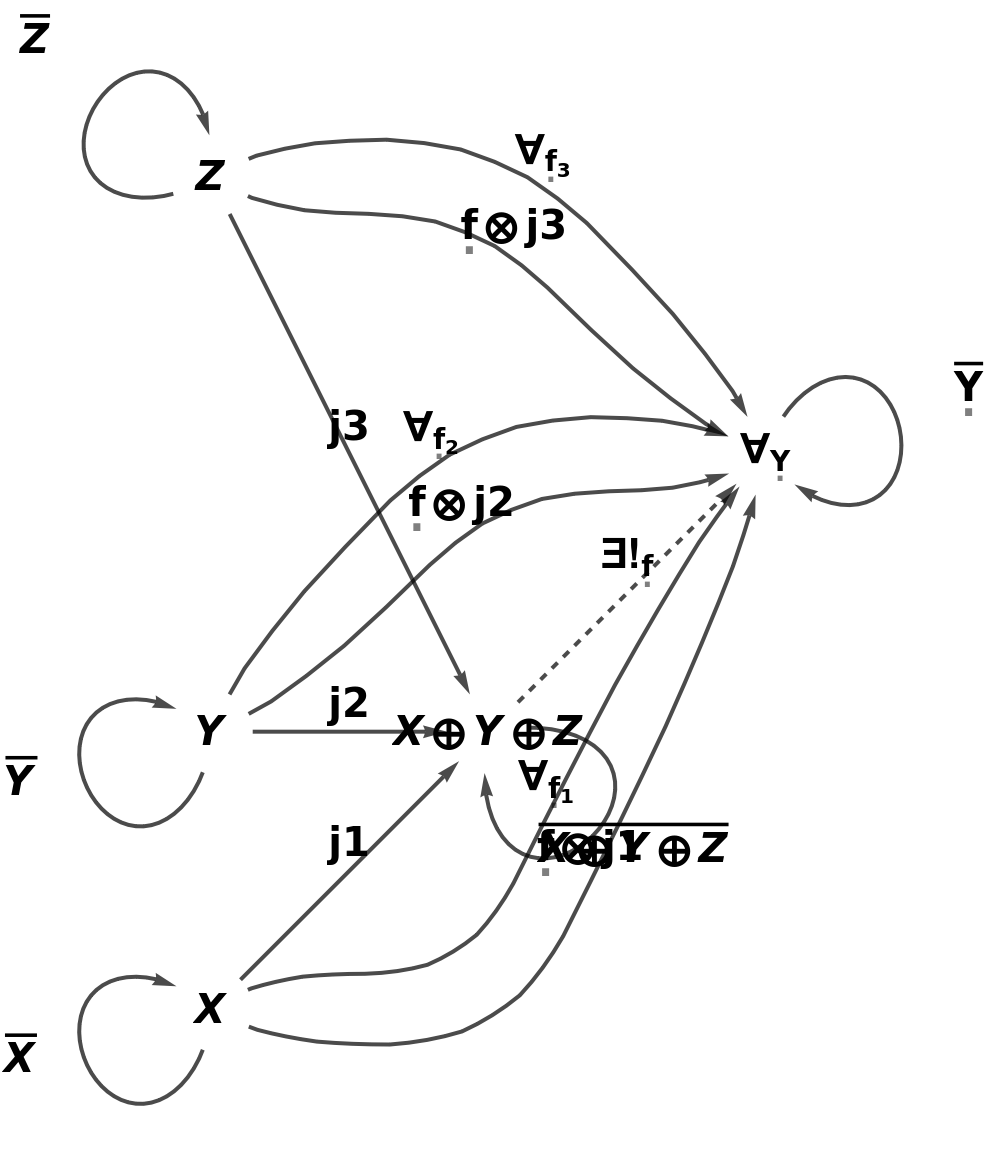

A universal object symbol, a list of universal morphisms and a unique morphism symbol can also be specified, in order to characterize the universal property fully:

In[33]:=
coproduct2 = ResourceFunction["AbstractCoproduct"][{X, Y, Z}, CirclePlus, {j1, j2, j3}, CircleTimes, OverBar, Q, {m1, m2, m3}, u]
Out[33]=
In[34]:=
coproduct2["UniversalFullLabeledGraph"]
Out[34]=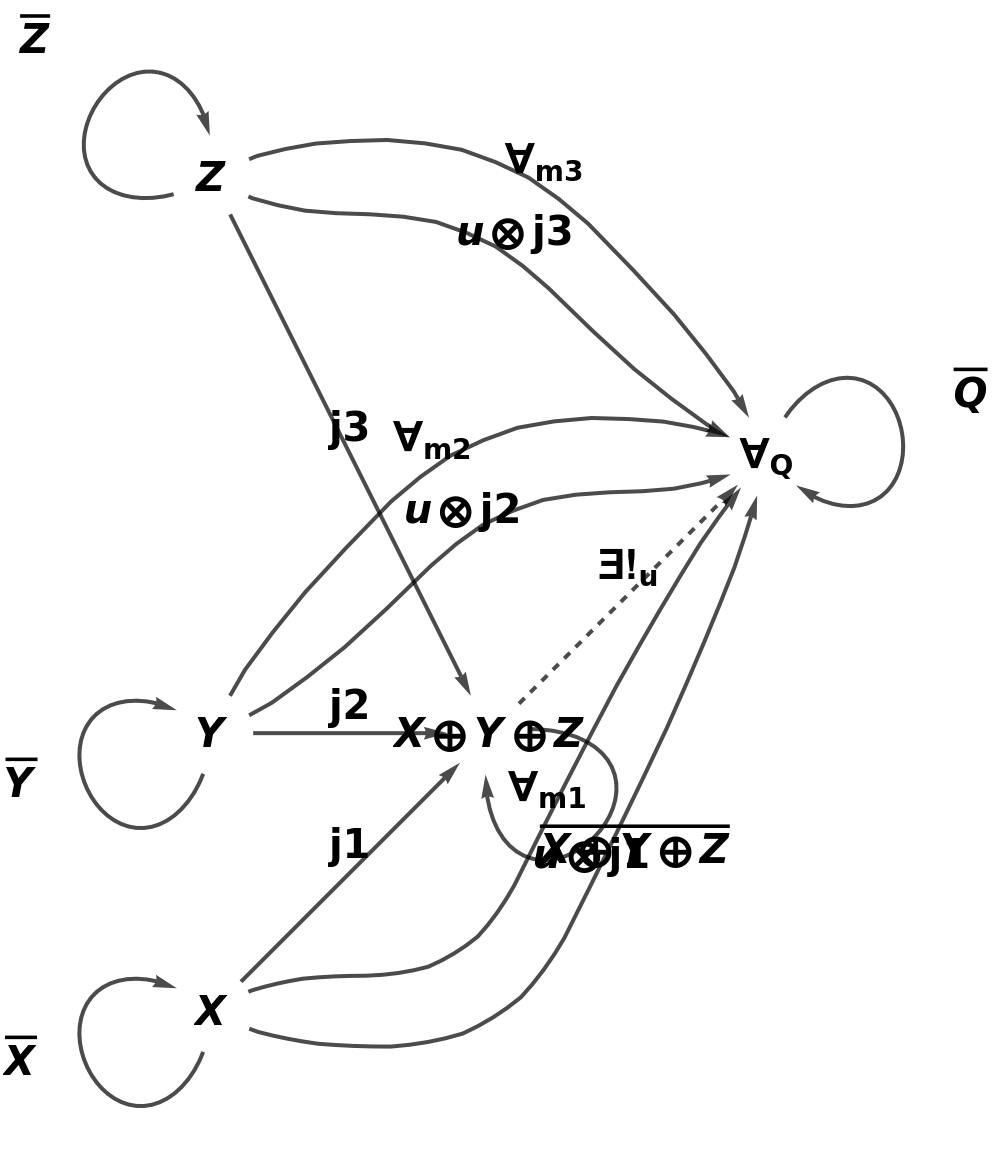

Abstract coproducts can also be constructed directly from a list of objects and a list of names of injection morphisms (plus composition and identity symbols):

In[35]:=
coproduct3 = ResourceFunction["AbstractCoproduct"][{X, Y}, {g1, g2}, CircleTimes, OverBar]
Out[35]=
In[36]:=
coproduct3["UniversalFullLabeledGraph"]
Out[36]=

Or from an object list with coproduct, composition and identity symbols alone:

In[37]:=
coproduct4 = ResourceFunction["AbstractCoproduct"][{X, Y}, CirclePlus, CircleTimes, OverBar]
Out[37]=
In[38]:=
coproduct4["UniversalFullLabeledGraph"]
Out[38]=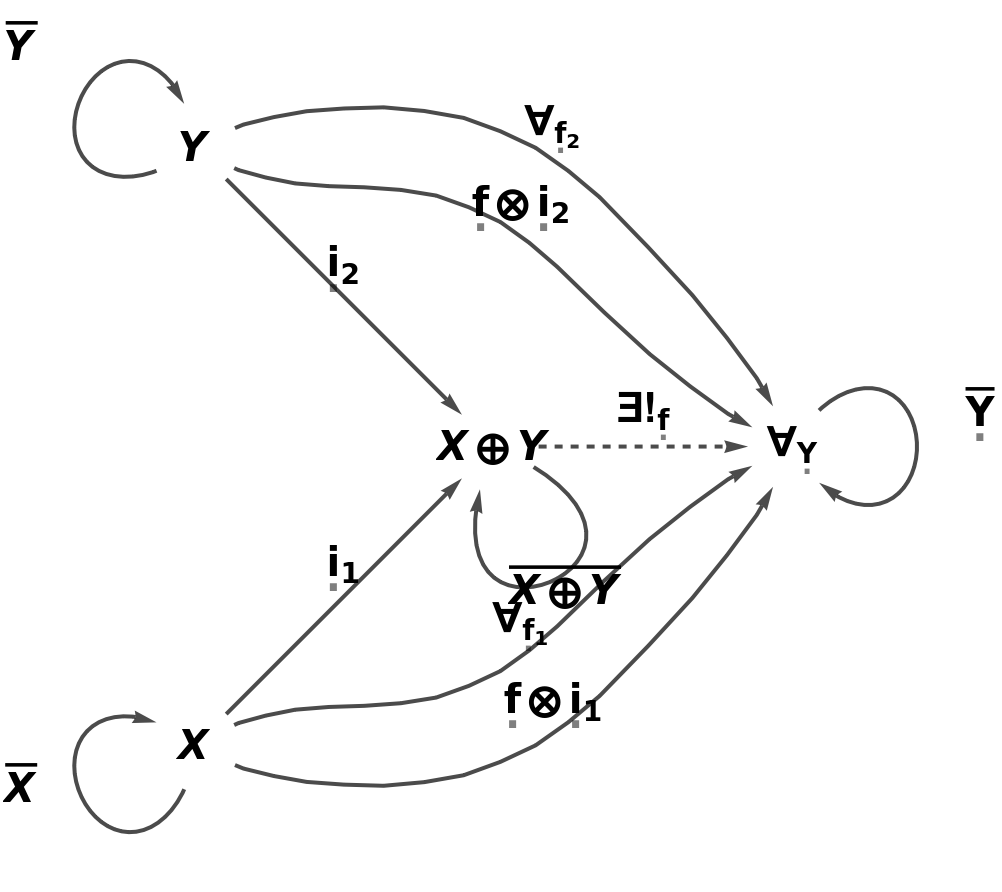

If any of these arguments is not fully specified, the appropriate defaults are assumed automatically:

In[39]:=
coproduct5 = ResourceFunction["AbstractCoproduct"][{U, V, W}]
Out[39]=
In[40]:=
coproduct5["UniversalFullLabeledGraph"]
Out[40]=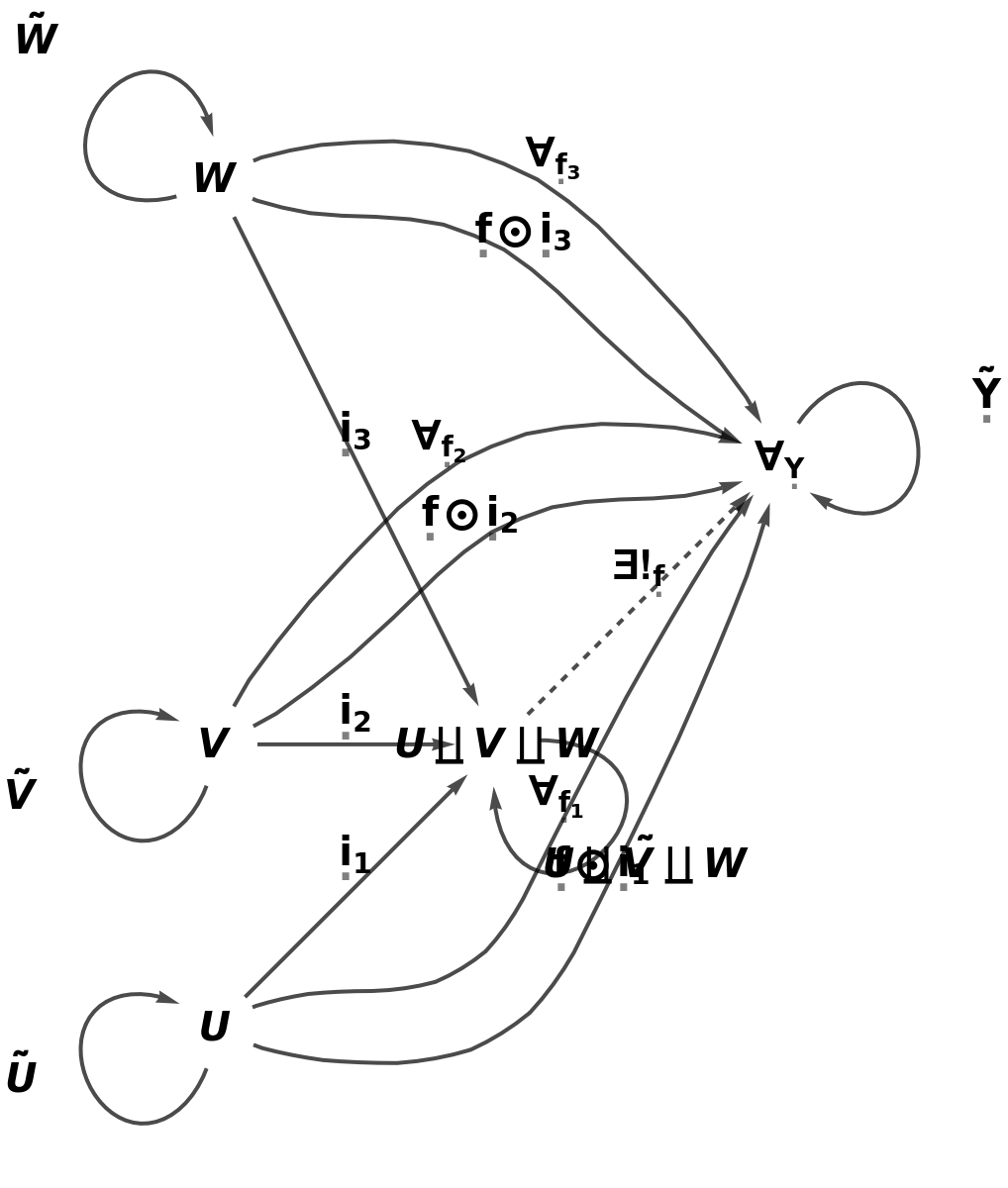

New coproduct, composition and identity symbols can be specified for any existing abstract coproduct:

In[41]:=
coproduct6 = ResourceFunction["AbstractCoproduct"][coproduct5, CirclePlus, CircleTimes, OverBar]
Out[41]=
In[42]:=
coproduct6["UniversalFullLabeledGraph"]
Out[42]=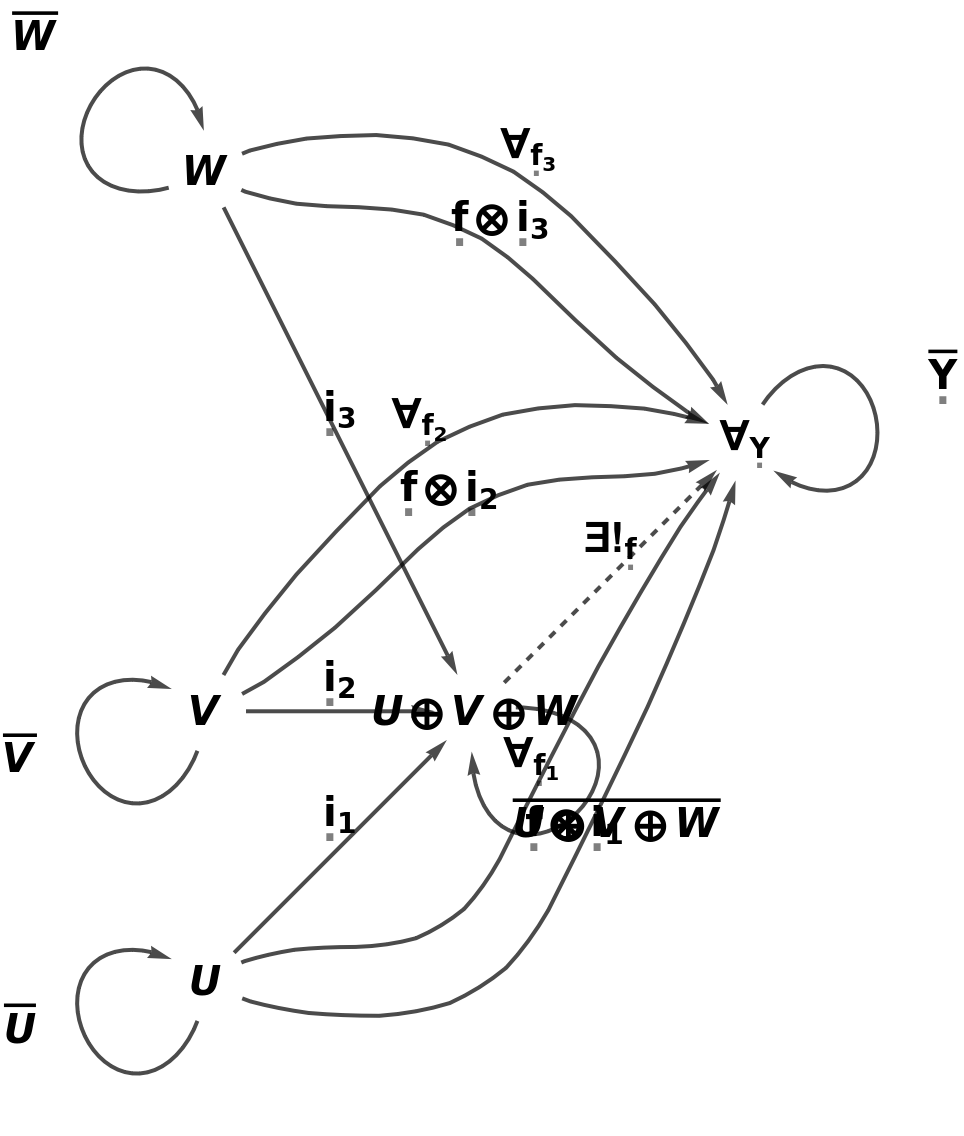

From an explicit association:

In[43]:=
ResourceFunction[ "AbstractCoproduct"][<|"Objects" -> {A, B}, "CoproductSymbol" -> CirclePlus, "InjectionMorphismNames" -> {j1, j2}, "CompositionSymbol" -> CircleTimes, "IdentitySymbol" -> OverBar, "UniversalObjectName" -> Q, "UniversalMorphismNames" -> {f1, f2}, "UniqueMorphismName" -> u|>]
Out[43]=

Construct an abstract coproduct of objects X, Y, Z and W:

In[44]:=
coproduct = ResourceFunction["AbstractCoproduct"][{X, Y, Z, W}]
Out[44]=

Show the list of properties:

In[45]:=
coproduct["Properties"]
Out[45]=

Show the list of objects in the abstract coproduct:

In[46]:=
coproduct["Objects"]
Out[46]=

Show the number of objects in the abstract coproduct:

In[47]:=
coproduct["ObjectCount"]
Out[47]=

Show the association of morphisms in the abstract coproduct:

In[48]:=
coproduct["MorphismAssociation"]
Out[48]=

Show the list of names of morphisms in the abstract coproduct:

In[49]:=
coproduct["MorphismNames"]
Out[49]=

Show the list of directed edges corresponding to morphisms in the abstract coproduct:

In[50]:=
coproduct["MorphismEdges"]
Out[50]=

Show the number of morphisms in the abstract coproduct:

In[51]:=
coproduct["MorphismCount"]
Out[51]=

Show the association of simple morphisms (with all self-loops removed) in the abstract coproduct:

In[52]:=
coproduct["SimpleMorphismAssociation"]
Out[52]=

Show the list of names of simple morphisms (with all self-loops removed) in the abstract coproduct:

In[53]:=
coproduct["SimpleMorphismNames"]
Out[53]=

Show the list of directed edges corresponding to simple morphisms (with all self-loops removed) in the abstract coproduct:

In[54]:=
coproduct["SimpleMorphismEdges"]
Out[54]=

Show the number of simple morphisms (with all self-loops removed) in the abstract coproduct:

In[55]:=
coproduct["SimpleMorphismCount"]
Out[55]=

Show the list of objects characterizing the universal property of the abstract coproduct:

In[56]:=
coproduct["UniversalObjects"]
Out[56]=

Show the number of objects characterizing the universal property of the abstract coproduct:

In[57]:=
coproduct["UniversalObjectCount"]
Out[57]=

Show the association of morphisms characterizing the universal property of the abstract coproduct:

In[58]:=
coproduct["UniversalMorphismAssociation"]
Out[58]=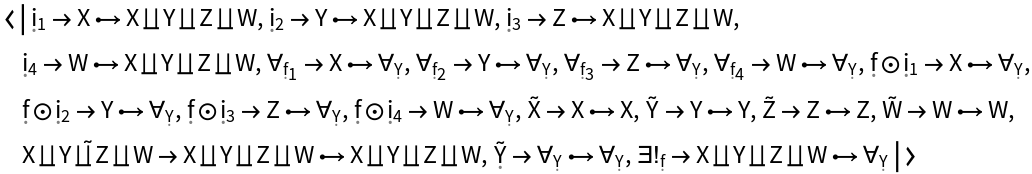

Show the list of names of morphisms characterizing the universal property of the abstract coproduct:

In[59]:=
coproduct["UniversalMorphismNames"]
Out[59]=

Show the list of directed edges corresponding to morphisms characterizing the universal property of the abstract coproduct:

In[60]:=
coproduct["UniversalMorphismEdges"]
Out[60]=

Show the number of morphisms characterizing the universal property of the abstract coproduct:

In[61]:=
coproduct["UniversalMorphismCount"]
Out[61]=

Show the association of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract coproduct:

In[62]:=
coproduct["UniversalReducedMorphismAssociation"]
Out[62]=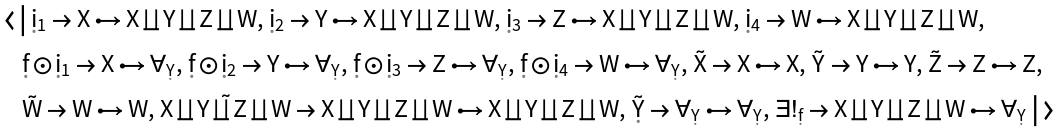

Show the list of names of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract coproduct:

In[63]:=
coproduct["UniversalReducedMorphismNames"]
Out[63]=

Show the list of directed edges corresponding to reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract coproduct:

In[64]:=
coproduct["UniversalReducedMorphismEdges"]
Out[64]=

Show the number of reduced morphisms (modded out by all morphism equivalences) characterizing the universal property of the abstract coproduct:

In[65]:=
coproduct["UniversalReducedMorphismCount"]
Out[65]=

Show the association of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract coproduct:

In[66]:=
coproduct["UniversalSimpleMorphismAssociation"]
Out[66]=

Show the list of names of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract coproduct:

In[67]:=
coproduct["UniversalSimpleMorphismNames"]
Out[67]=

Show the list of directed edges corresponding to simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract coproduct:

In[68]:=
coproduct["UniversalSimpleMorphismEdges"]
Out[68]=

Show the number of simple morphisms (with all self-loops and multiedges removed) characterizing the universal property of the abstract coproduct:

In[69]:=
coproduct["UniversalSimpleMorphismCount"]
Out[69]=

Show the association of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract coproduct:

In[70]:=
coproduct["UniversalReducedSimpleMorphismAssociation"]
Out[70]=

Show the list of names of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract coproduct:

In[71]:=
coproduct["UniversalReducedSimpleMorphismNames"]
Out[71]=

Show the list of directed edges corresponding to reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract coproduct:

In[72]:=
coproduct["UniversalReducedSimpleMorphismEdges"]
Out[72]=

Show the number of reduced simple morphisms (with all self-loops and multiedges removed, plus all morphism equivalences modded out) characterizing the universal property of the abstract coproduct:

In[73]:=
coproduct["UniversalReducedSimpleMorphismCount"]
Out[73]=

Show the (arbitrary arity) symbol used to denote the abstract coproduct operation:

In[74]:=
coproduct["CoproductSymbol"]
Out[74]=

Show the (binary) symbol used to denote morphism composition in the abstract coproduct:

In[75]:=
coproduct["CompositionSymbol"]
Out[75]=

Show the (unary) symbol used to denote identity morphisms on objects in the abstract coproduct:

In[76]:=
coproduct["IdentitySymbol"]
Out[76]=

Compute the abstract category whose morphisms represent the abstract coproduct:

In[77]:=
coproduct["CoproductCategory"]
Out[77]=

Compute the abstract category whose morphisms characterize the universal property of the abstract coproduct:

In[78]:=
coproduct["UniversalCoproductCategory"]
Out[78]=

Show the list of equations imposed implicitly by the requirement that the universal property of the abstract coproduct is satisfied:

In[79]:=
coproduct["UniversalCoproductEquations"]
Out[79]=

Show the full directed graph with labels on the morphisms of the abstract coproduct:

In[80]:=
coproduct["FullLabeledGraph"]
Out[80]=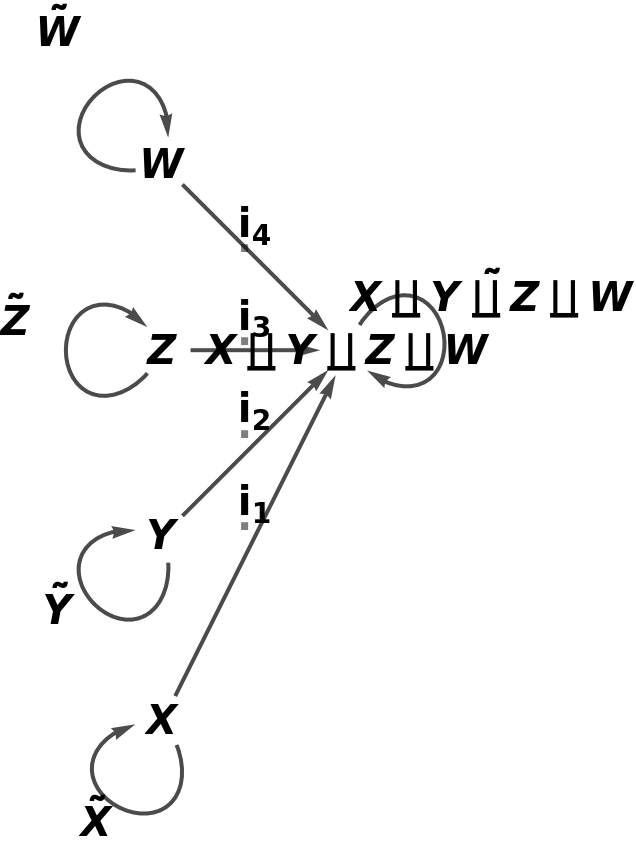

Show the full directed graph without labels on the morphism of the abstract coproduct:

In[81]:=
coproduct["FullUnlabeledGraph"]
Out[81]=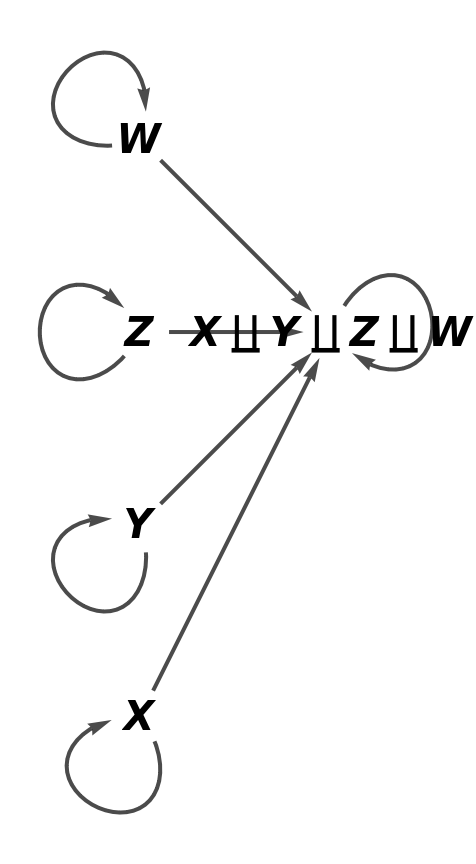

Show the simple directed graph, with all self-loops removed and with labels on the morphisms of the abstract coproduct:

In[82]:=
coproduct["SimpleLabeledGraph"]
Out[82]=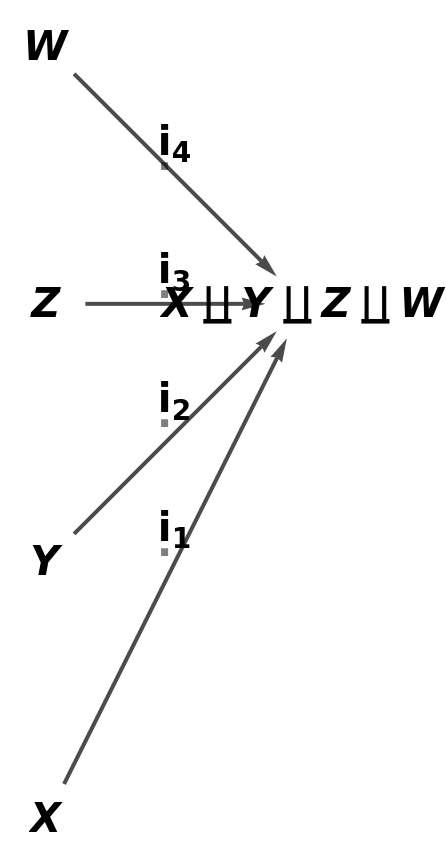

Show the simple directed graph, with all self-loops removed and without labels on the morphisms of the abstract coproduct:

In[83]:=
coproduct["SimpleUnlabeledGraph"]
Out[83]=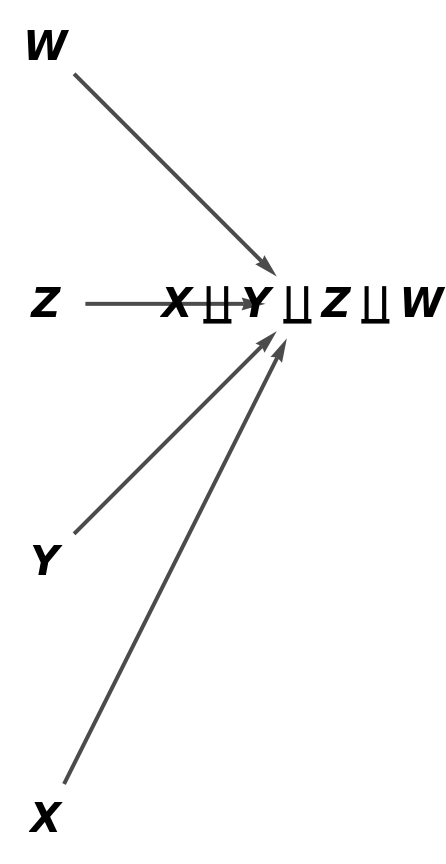

Show the full directed graph characterizing the universal property of the abstract coproduct, with labels on the morphisms:

In[84]:=
coproduct["UniversalFullLabeledGraph"]
Out[84]=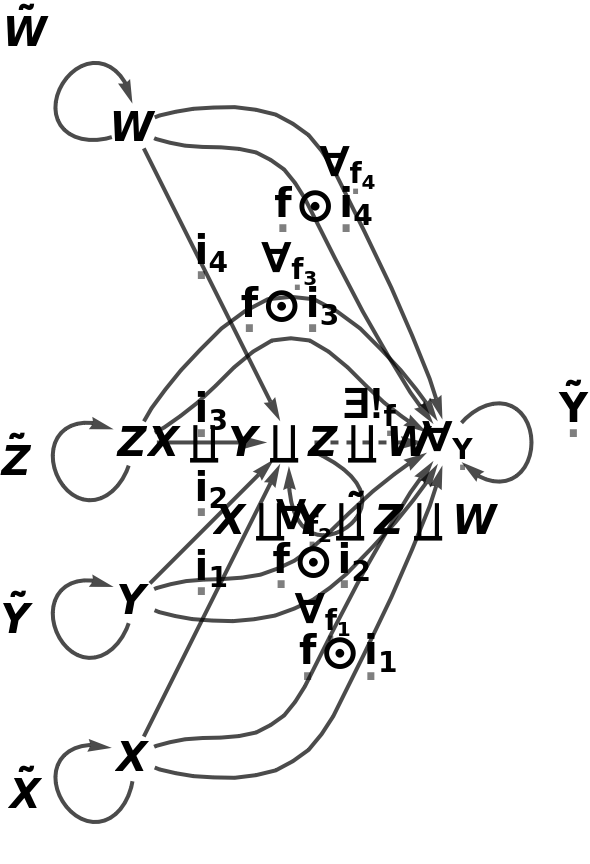

Show the full directed graph characterizing the universal property of the abstract coproduct, without labels on the morphisms:

In[85]:=
coproduct["UniversalFullUnlabeledGraph"]
Out[85]=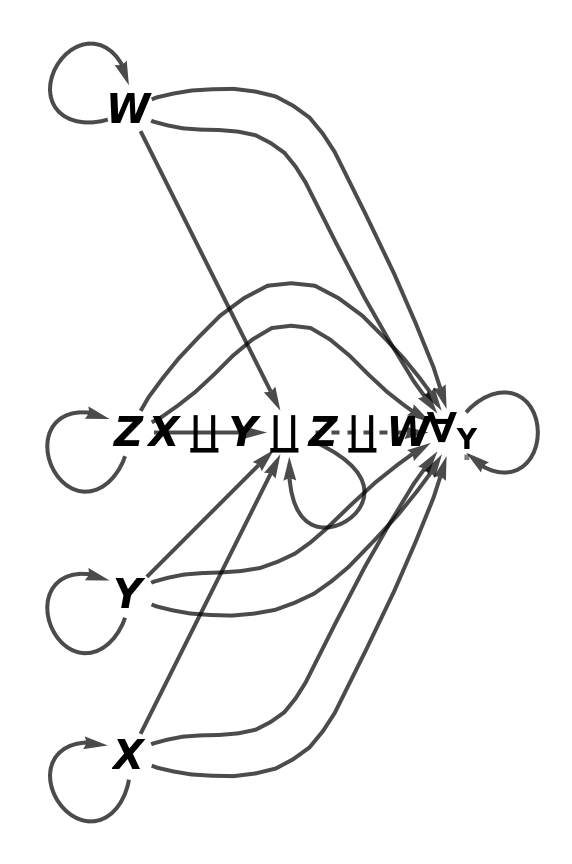

Show the reduced directed graph characterizing the universal property of the abstract coproduct, with all equivalences between morphisms imposed and with labels on the morphisms:

In[86]:=
coproduct["UniversalReducedLabeledGraph"]
Out[86]=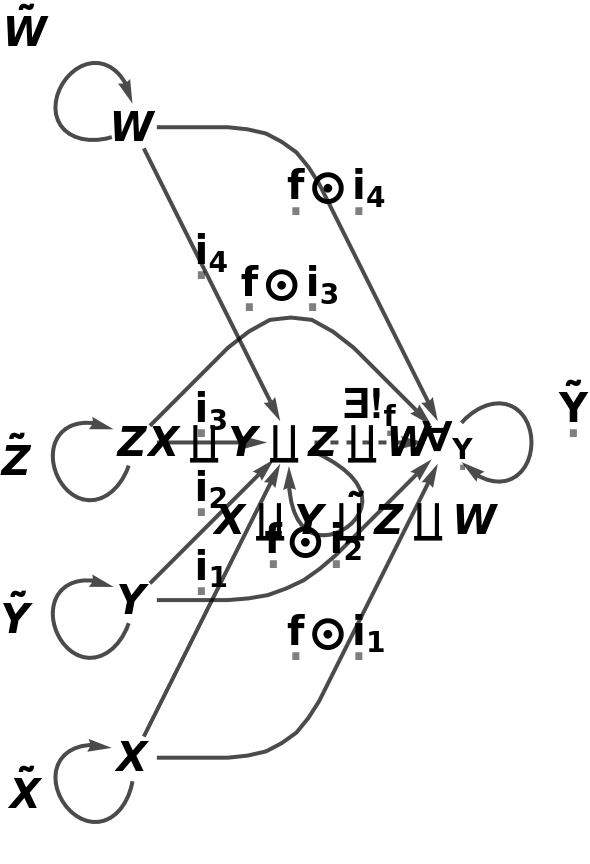

Show the reduced directed graph characterizing the universal property of the abstract coproduct, with all equivalences between morphisms imposed and without labels on the morphisms:

In[87]:=
coproduct["UniversalReducedUnlabeledGraph"]
Out[87]=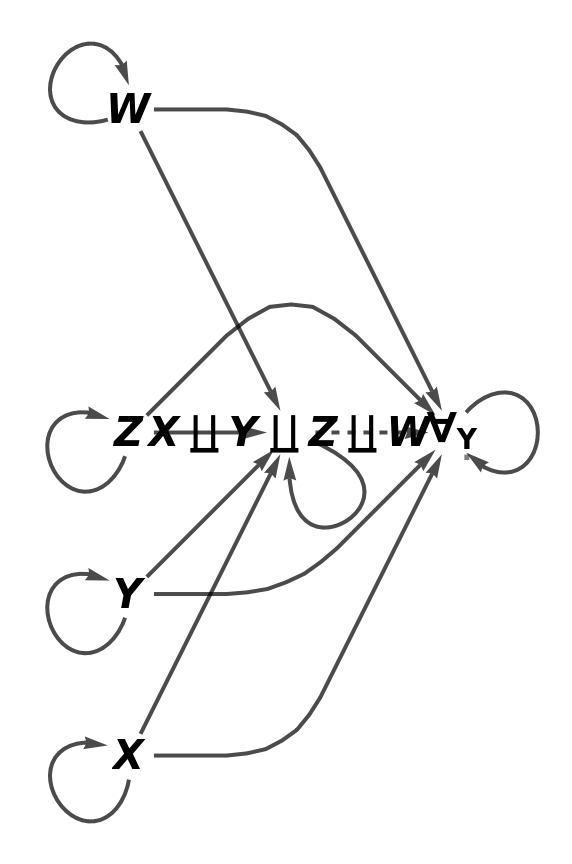

Show the simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed and with labels on the morphisms:

In[88]:=
coproduct["UniversalSimpleLabeledGraph"]
Out[88]=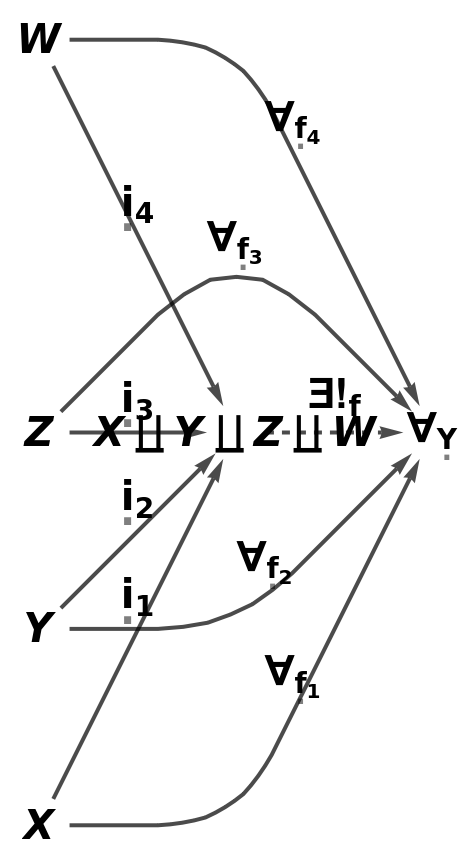

Show the simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed and without labels on the morphisms:

In[89]:=
coproduct["UniversalSimpleUnlabeledGraph"]
Out[89]=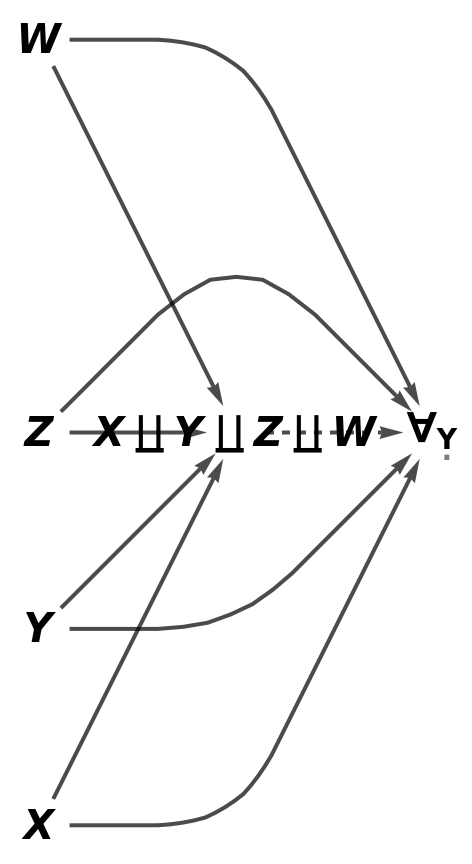

Show the reduced simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and with labels on the morphisms:

In[90]:=
coproduct["UniversalReducedSimpleLabeledGraph"]
Out[90]=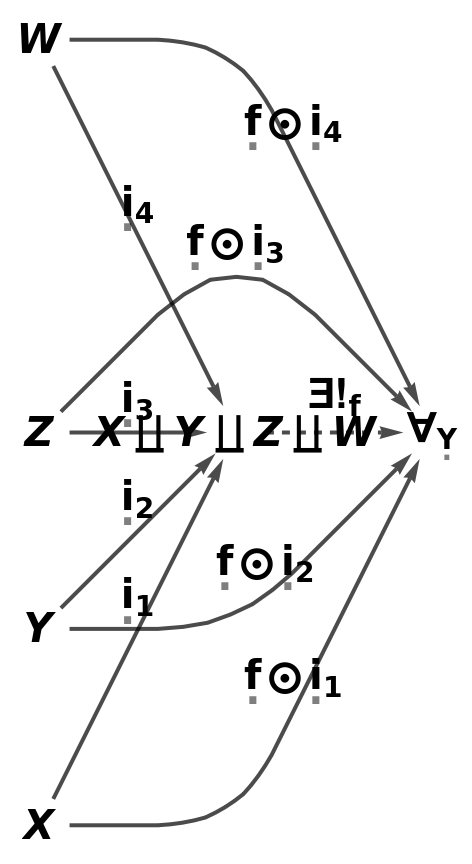

Show the reduced simple directed graph characterizing the universal property of the abstract coproduct, with all self-loops and multiedges removed, plus all equivalences between morphisms modded out and without labels on the morphisms:

In[91]:=
coproduct["UniversalReducedSimpleUnlabeledGraph"]
Out[91]=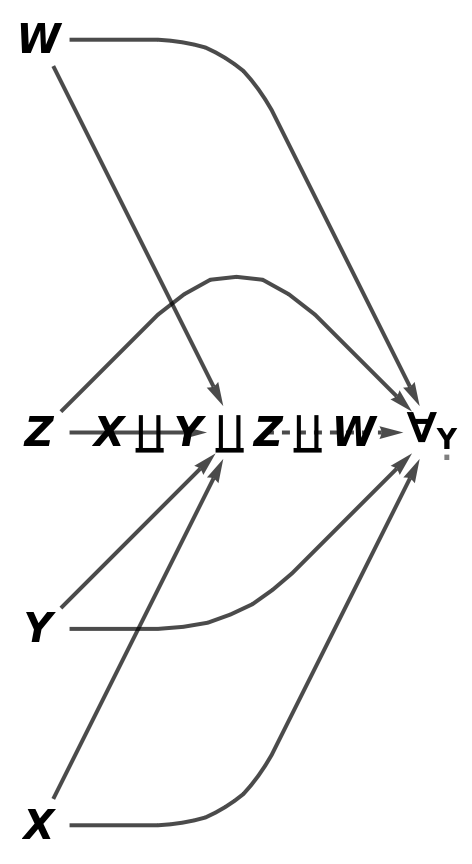

Show the explicit association form of the coproduct:

In[92]:=
coproduct["AssociationForm"]
Out[92]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 22 April 2022

Source Metadata

  • Citation:
    • Saunders Mac Lane (1971), Categories for the Working Mathematician
    • Stephen Wolfram (2002), A New Kind of Science
    • Stephen Wolfram (2020), "A Class of Models with the Potential to Represent Fundamental Physics"
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

License Information