Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Obtain the parameters for orbital motion
ResourceFunction["OrbitalProperties"][e,M] returns the results for orbital motion given eccentricity e and mean anomaly M. | |
ResourceFunction["OrbitalProperties"][e,M,"format"] returns the results for orbital motion in the specific format. |
| "Association" | (default) return the results for orbital motion |
| "RelationPlot" | plot of the relation between eccentric anomaly and true anomaly |
| "AngleUnit" | "AngularDegrees" | specify the angle unit used in the "Association" output form |
| "LengthUnit" | "Kilometers" | specify the length unit used in the "Association" output form |
| "SemimajorAxis" | Quantity[10000,"Kilometers"] | specify the value of the semimajor axis used to compute to radial position |
Results for orbital motion:
| In[1]:= |
| Out[1]= |
Specify the output form as an Association:
| In[2]:= |
| Out[2]= |
Find the relation between eccentric anomaly and true anomaly:
| In[3]:= |
| Out[3]= | 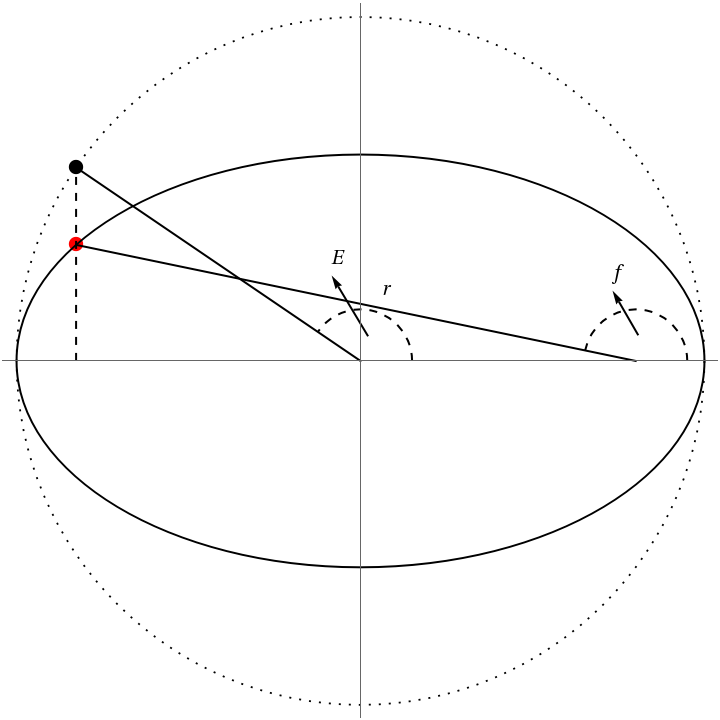 |
Use "AngleUnit" to specify the output angle unit in the Association form:
| In[4]:= |
| Out[4]= |
Use "LengthUnit" to specify the output length unit in the Association form:
| In[5]:= |
| Out[5]= |
Use "SemimajorAxis" to specify the value of the semimajor axis used to compute the radial position:
| In[6]:= |
| Out[6]= |
Visualize the progress of an orbiting body over 52 weeks:
| In[7]:= | ![KeplerOrbit[ph_, eps_] := With[{ea = QuantityMagnitude@
ResourceFunction["OrbitalProperties"] [eps, ph][
"EccentricAnomaly"]}, {eps + Cos[ea], Sqrt[1 - eps^2] Sin[ea]}];
With[{n = 52, \[CurlyEpsilon] = Sqrt[1/2]},
Graphics[
{Table[{RandomChoice[ColorData[113, "ColorList"]], Polygon[Prepend[
KeplerOrbit[#, \[CurlyEpsilon]] & /@ Range[w, w + 2 \[Pi]/n, 2 \[Pi]/(7 n)], {0, 0}]]}, {w, \[Pi]/
n, \[Pi] (2 - 1/n), 2 \[Pi]/n}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/fc5/fc5ee2f9-c7ce-46f6-af2d-e5a93d2369ce/79168c74292415f1.png) |
| Out[7]= | 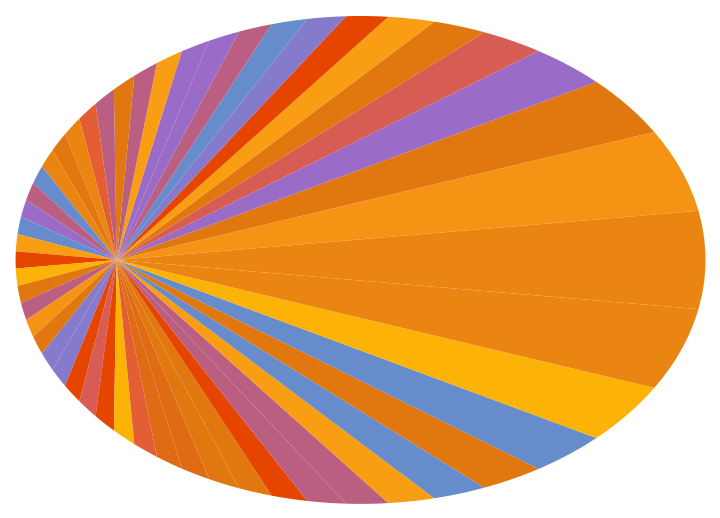 |
This work is licensed under a Creative Commons Attribution 4.0 International License