Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Make an abstract model of a quiver (i.e. a directed multigraph) that forms the basis of an abstract category
ResourceFunction["AbstractQuiver"][ob,arr,eqob,eqarr] makes an abstract quiver using the list of objects ob, the list or association of arrows arr, the list of object equivalences eqob and the list of arrow equivalences eqarr. | |
ResourceFunction["AbstractQuiver"][gr,…] makes an abstract quiver based on the directed graph gr. | |
ResourceFunction["AbstractQuiver"][assoc] makes an abstract quiver using the association of objects, arrows, object equivalences and arrow equivalences assoc. | |
ResourceFunction["AbstractQuiver"][ResourceFunction["AbstractQuiver"][…],eqob,eqarr] makes a new abstract quiver from an old quiver by imposing new object equivalences eqob and new arrow equivalences eqarr. |
| "Objects" | list of objects in the abstract quiver |
| "ObjectCount" | number of objects in the abstract quiver |
| "ArrowAssociation" | association of arrow names/edges in the abstract quiver |
| "ArrowNames" | list of names of arrows in the abstract quiver |
| "ArrowEdges" | list of directed edges associated to arrows in the abstract quiver |
| "ArrowCount" | number of arrows in the abstract quiver |
| "ObjectEquivalences" | list of equivalences between objects in the abstract quiver |
| "ObjectEquivalenceCount" | number of equivalences between objects in the abstract quiver |
| "ArrowEquivalences" | list of equivalences between arrows in the abstract quiver |
| "ArrowEquivalenceCount" | number of equivalences between arrows in the abstract quiver |
| "ReducedObjects" | list of objects in the abstract quiver modulo the list of object equivalences |
| "ReducedObjectCount" | number of objects in the abstract quiver modulo the list of object equivalences |
| "ReducedArrowAssociation" | association of arrow names/edges in the abstract quiver modulo the lists of arrow/object equivalences |
| "ReducedArrowNames" | list of names of arrows in the abstract quiver modulo the list of arrow equivalences |
| "ReducedArrowEdges" | list of directed edges associated to arrows in the abstract quiver modulo the lists of arrow/object equivalences |
| "ReducedArrowCount" | number of arrows in the abstract quiver modulo the list of arrow equivalences |
| "SimpleArrowAssociation" | association of arrow names/edges in the abstract quiver with self-loops and multiedges removed |
| "SimpleArrowNames" | list of names of arrows in the abstract quiver with self-loops and multiedges removed |
| "SimpleArrowEdges" | list of directed edges associated to arrows in the abstract quiver with self-loops and multiedges removed |
| "SimpleArrowCount" | number of arrows in the abstract quiver with self-loops and multiedges removed |
| "ReducedSimpleArrowAssociation" | association of arrow names/edges in the abstract quiver with self-loops and multiedges removed, modulo the lists of arrow/object equivalences |
| "ReducedSimpleArrowNames" | list of names of arrows in the abstract quiver with self-loops and multiedges removed, modulo the list of arrow equivalences |
| "ReducedSimpleArrowEdges" | list of directed edges associated to arrows in the abstract quiver with self-loops and multiedges removed, modulo the lists of arrow/object equivalences |
| "ReducedSimpleArrowCount" | number of arrows in the abstract quiver with self-loops and multiedges removed, modulo the list of arrow equivalences |
| "DualQuiver" | dual quiver (i.e. the abstract quiver obtained by swapping the source and target objects of all the arrows) |
| "FullLabeledGraph" | directed graph form of the abstract quiver with labels on the arrows |
| "FullUnlabeledGraph" | directed graph form of the abstract quiver with no labels on the arrows |
| "ReducedLabeledGraph" | directed graph form of the abstract quiver, modulo the lists of arrow/object equivalences, with labels on the arrows |
| "ReducedUnlabeledGraph" | directed graph form of the abstract quiver, modulo the lists of arrow/object equivalences, with no labels on the arrows |
| "SimpleLabeledGraph" | directed graph form of the abstract quiver, with self-loops and multiedges removed, with labels on the arrows |
| "SimpleUnlabeledGraph" | directed graph form of the abstract quiver, with self-loops and multiedges removed, with no labels on the arrows |
| "ReducedSimpleLabeledGraph" | directed graph form of the abstract quiver, with self-loops and multiedges removed, modulo the lists of arrow/object equivalences, with labels on the arrows |
| "ReducedSimpleUnlabeledGraph" | directed graph form of the abstract quiver, with self-loops and multiedges removed, modulo the lists of arrow/object equivalences, with no labels on the arrows |
| "AssociationForm" | abstract quiver represented as an association of objects, arrows, object equivalences and arrow equivalences |
| "Properties" | list of properties |
Construct a simple abstract quiver from an association of arrows:
| In[1]:= |
| Out[1]= |
Show the full directed graph with labels on the arrows:
| In[2]:= |
| Out[2]= | 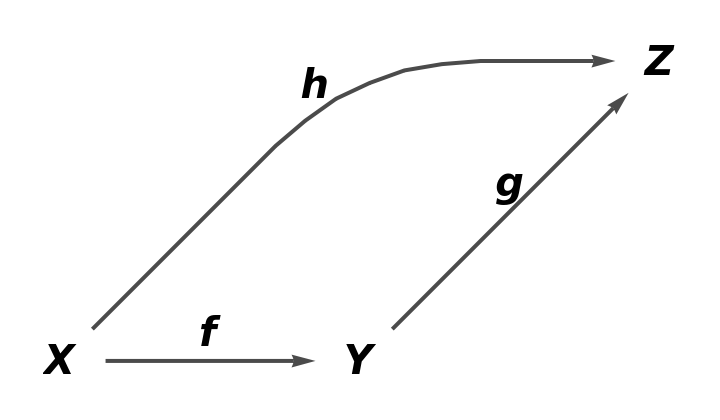 |
Show the full directed graph without labels on the arrows:
| In[3]:= |
| Out[3]= | 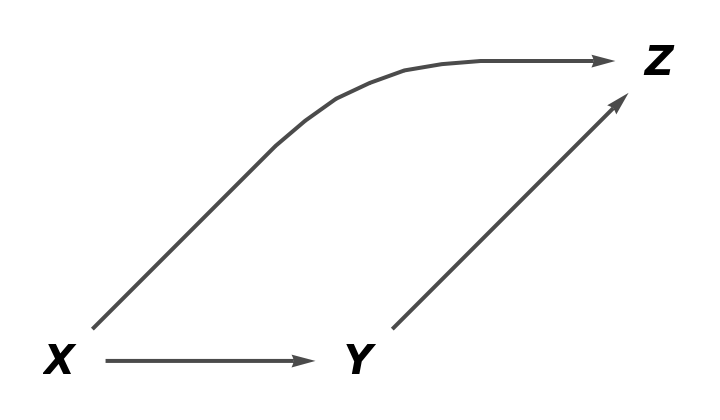 |
Show the association of arrows:
| In[4]:= |
| Out[4]= |
Show the list of directed edges:
| In[5]:= |
| Out[5]= |
Show the list of objects:
| In[6]:= |
| Out[6]= |
Construct an abstract quiver containing self-loops and multiedges from a list of objects and a list of arrows:
| In[7]:= |
| Out[7]= |
Show the full directed graph with labels on the arrows:
| In[8]:= |
| Out[8]= | 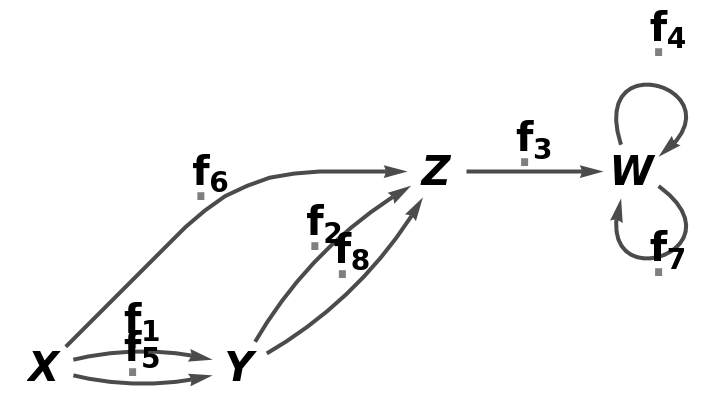 |
Show the full labeled graph without labels on the arrows:
| In[9]:= |
| Out[9]= | 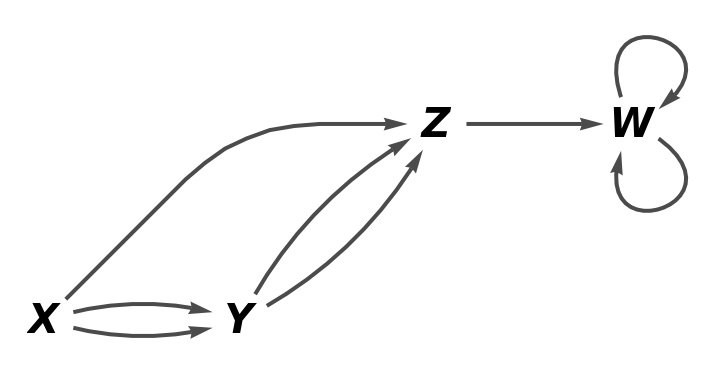 |
Show the association of arrows:
| In[10]:= |
| Out[10]= |
Show the simple directed graph with all self-loops and multiedges removed and with labels on the arrows:
| In[11]:= |
| Out[11]= | 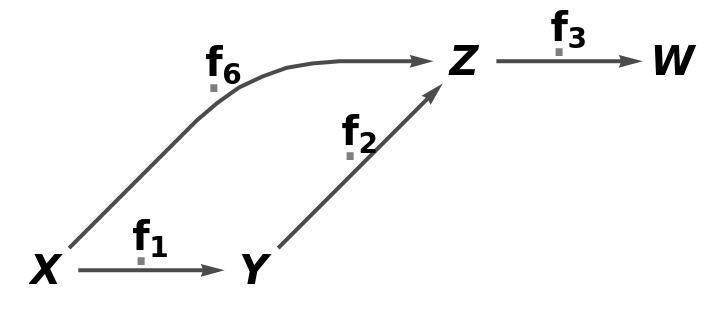 |
Show the simple directed graph but without labels on the arrows:
| In[12]:= |
| Out[12]= | 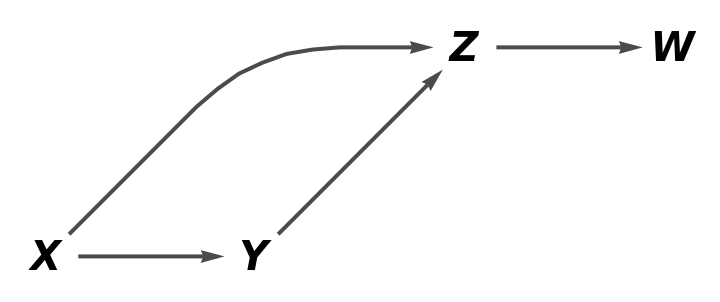 |
Show the association of arrows, with all self-loops and multiedges removed:
| In[13]:= |
| Out[13]= |
Compute the dual quiver (obtained by swapping the source and target objects of each arrow):
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= | 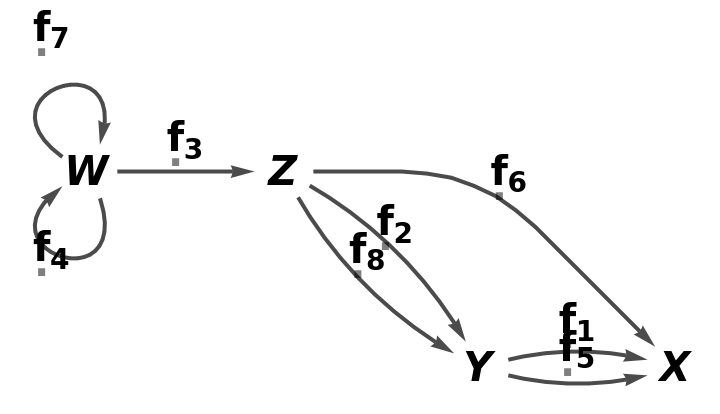 |
| In[16]:= |
| Out[16]= | 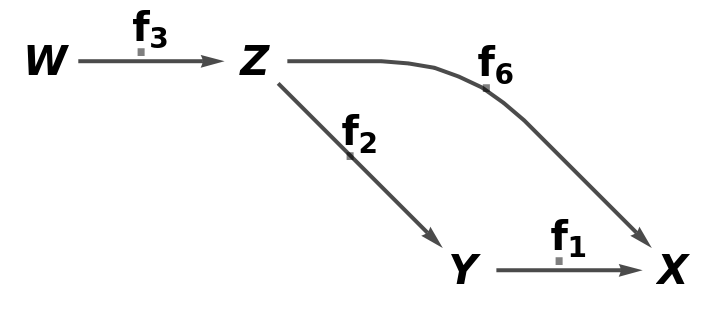 |
Construct an abstract quiver from an association of arrows, with an equivalence imposed between objects Z and W:
| In[17]:= |
| Out[17]= |
Show the full directed graph with labels on the arrows:
| In[18]:= |
| Out[18]= | 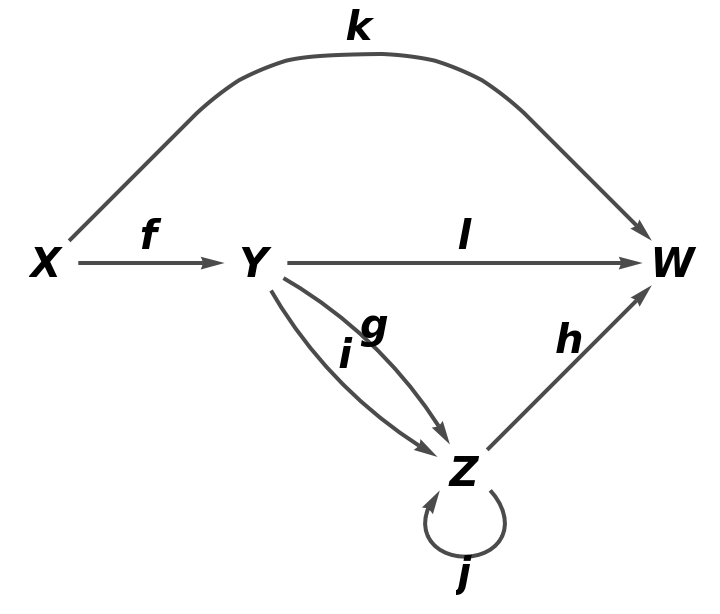 |
Show the full directed graph without labels on the arrows:
| In[19]:= |
| Out[19]= | 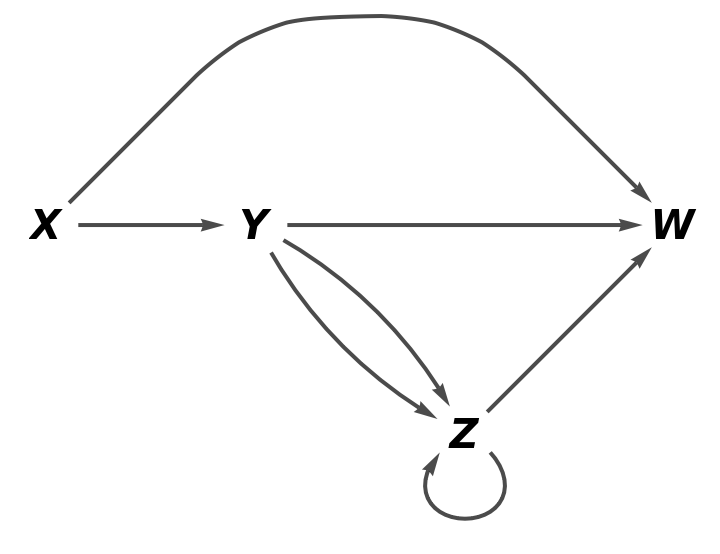 |
Show the reduced directed graph, with all equivalences between objects and arrows imposed and with labels on the arrows:
| In[20]:= |
| Out[20]= | 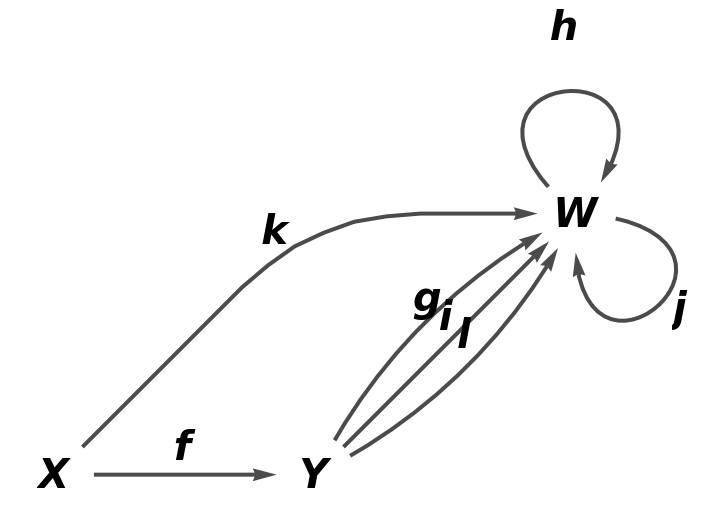 |
Show the reduced directed graph without labels on the arrows:
| In[21]:= |
| Out[21]= | 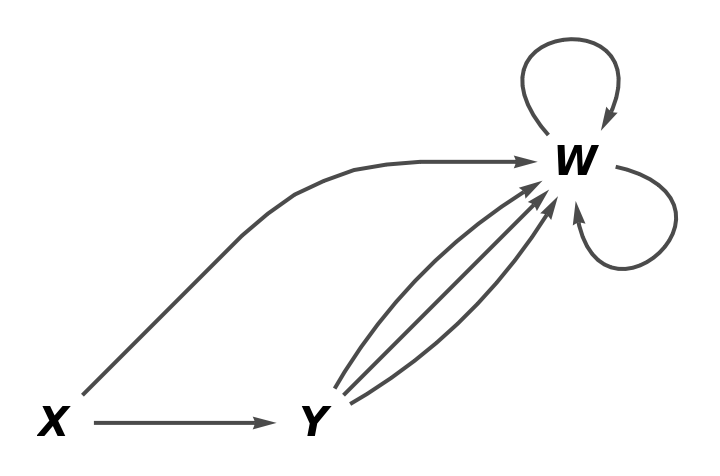 |
Show the association of arrows, with all equivalences between objects and arrows imposed:
| In[22]:= |
| Out[22]= |
Construct the same abstract quiver, but with an additional equivalence imposed between arrows g, i and l:
| In[23]:= |
| Out[23]= |
Show the reduced directed graph, with all equivalences between objects and arrows imposed and with labels on the arrows:
| In[24]:= |
| Out[24]= | 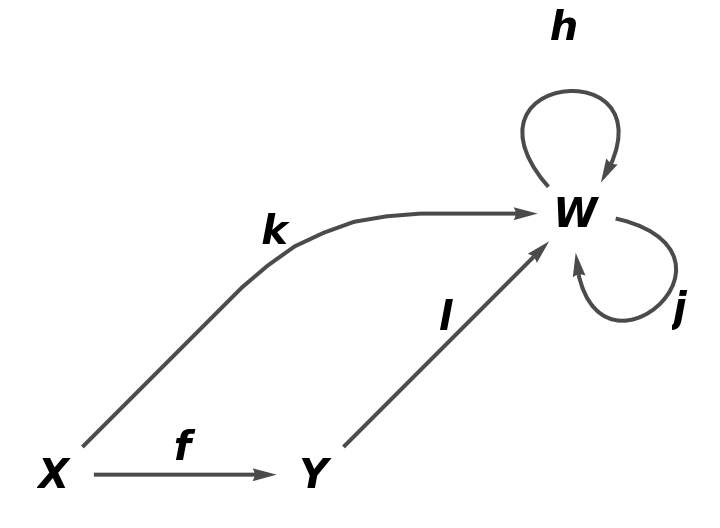 |
Show the reduced directed graph without labels on the arrows:
| In[25]:= |
| Out[25]= | 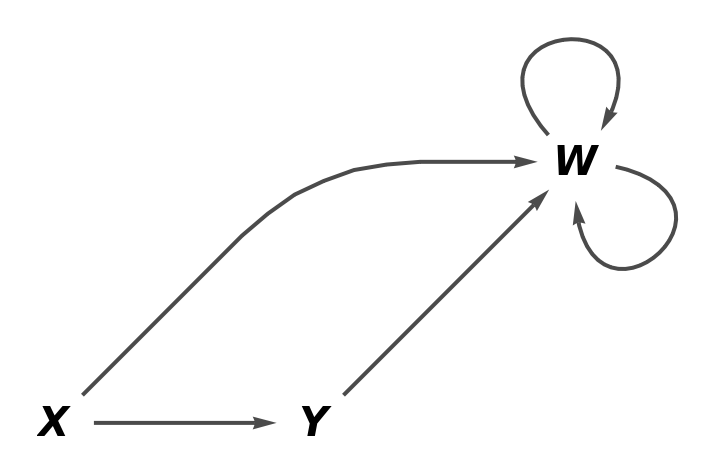 |
Show the association of arrows, with all equivalences between objects and arrows imposed:
| In[26]:= |
| Out[26]= |
Show the list of equivalences between objects:
| In[27]:= |
| Out[27]= |
Show the list of equivalences between arrows:
| In[28]:= |
| Out[28]= |
Show the association form of the abstract quiver:
| In[29]:= |
| Out[29]= |
Abstract quivers can be constructed directly from directed graph objects (with automatically selected arrow names):
| In[30]:= |
| Out[30]= | 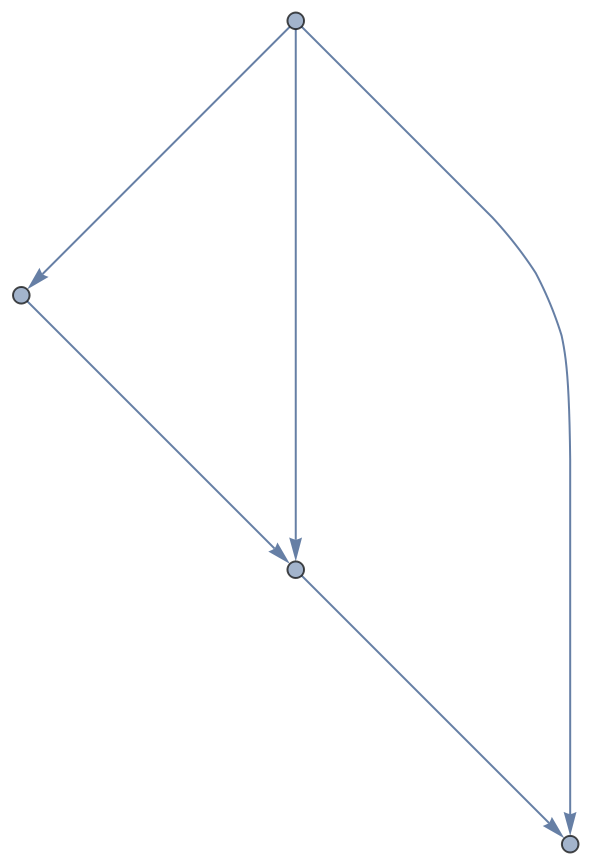 |
| In[31]:= |
| Out[31]= |
| In[32]:= |
| Out[32]= | 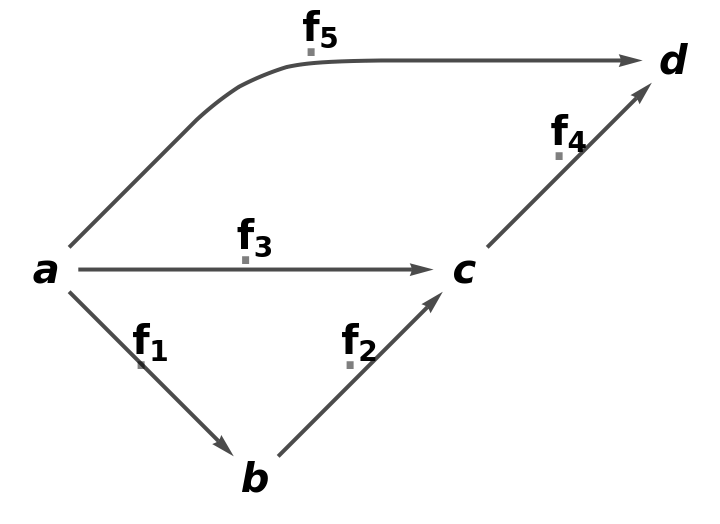 |
Additional arguments can be used to specify equivalences between objects and arrows:
| In[33]:= |
| Out[33]= |
| In[34]:= |
| Out[34]= | 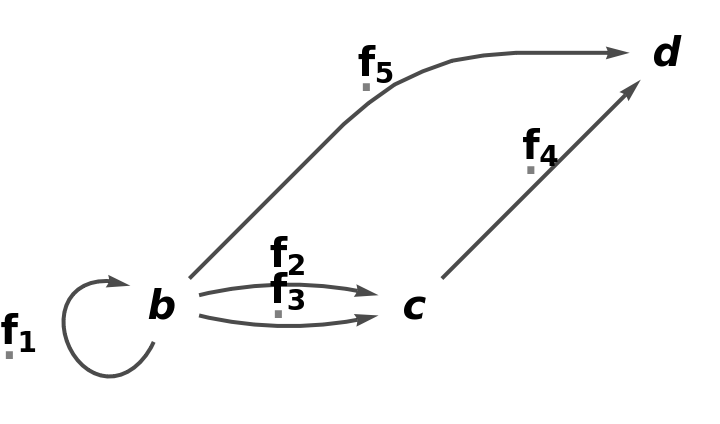 |
Abstract quivers can be constructed from lists of arrows (with automatically selected arrow names):
| In[35]:= |
| Out[35]= |
| In[36]:= |
| Out[36]= | 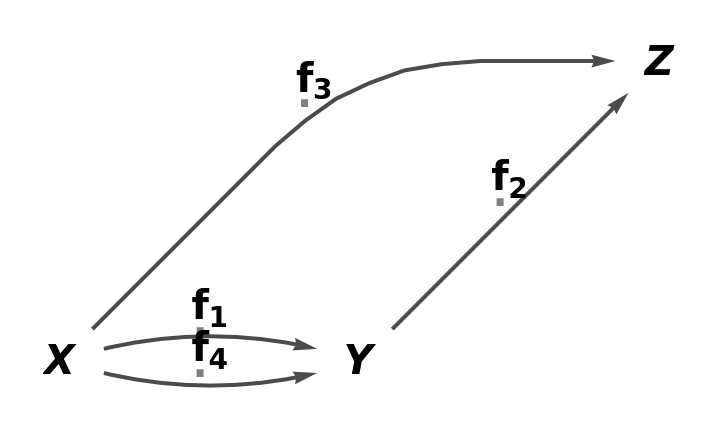 |
From associations of arrows (with explicitly provided arrow names):
| In[37]:= |
| Out[37]= |
| In[38]:= |
| Out[38]= |  |
With explicit lists of objects specified:
| In[39]:= |
| Out[39]= |
| In[40]:= |
| Out[40]= | 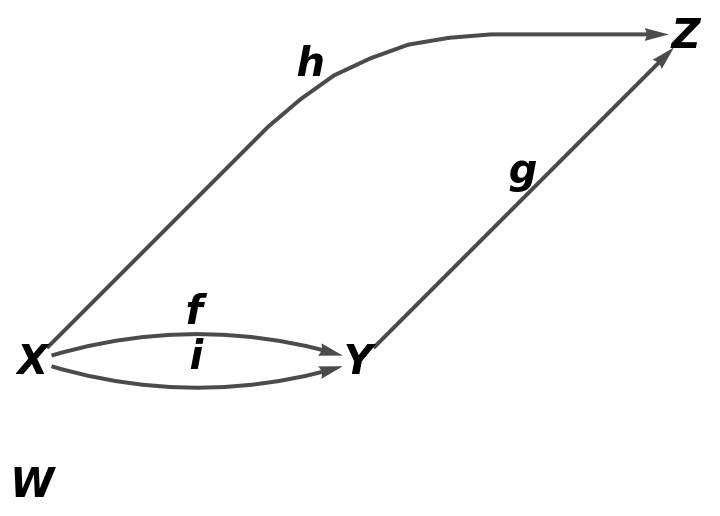 |
Lists of object equivalences and arrow equivalences can be specified for any abstract quiver:
| In[41]:= |
| Out[41]= |
| In[42]:= |
| Out[42]= | 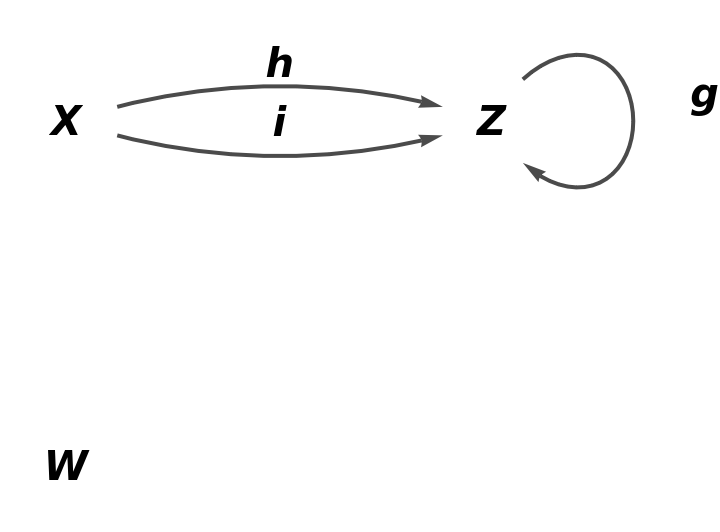 |
New object equivalences and arrow equivalences can be added to any existing quiver:
| In[43]:= |
| Out[43]= |
| In[44]:= |
| Out[44]= | 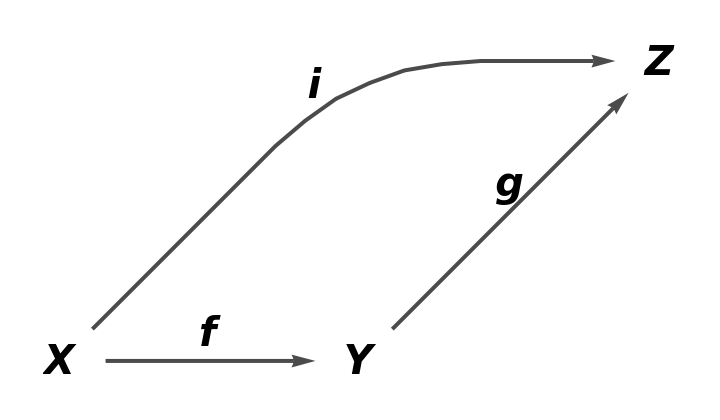 |
From an explicit association:
| In[45]:= | ![quiver5 = ResourceFunction[
"AbstractQuiver"][<|"Objects" -> {X, Y, Z}, "Arrows" -> <|f -> {X, Y}, g -> {Y, Z}, h -> {X, Z}, i -> {Y, Z}|>,
"ObjectEquivalences" -> {}, "ArrowEquivalences" -> {}|>]](https://www.wolframcloud.com/obj/resourcesystem/images/fba/fbae3943-d829-461d-806d-7577b78b4384/5efa03e8ac516c93.png) |
| Out[45]= |
| In[46]:= |
| Out[46]= | 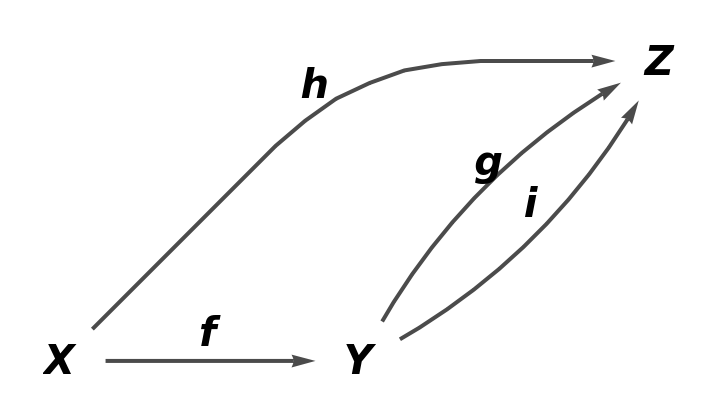 |
Construct an abstract quiver from an association of arrows with additional object and arrow equivalences:
| In[47]:= |
| Out[47]= |
Show the list of properties:
| In[48]:= |
| Out[48]= |  |
Show the list of objects in the abstract quiver:
| In[49]:= |
| Out[49]= |
Show the number of objects in the abstract quiver:
| In[50]:= |
| Out[50]= |
Show the association of arrows in the abstract quiver:
| In[51]:= |
| Out[51]= |
Show the list of names of arrows in the abstract quiver:
| In[52]:= |
| Out[52]= |
Show the list of directed edges corresponding to arrows in the abstract quiver:
| In[53]:= |
| Out[53]= |
Show the number of arrows in the abstract quiver:
| In[54]:= |
| Out[54]= |
Show the list of equivalences between objects in the abstract quiver:
| In[55]:= |
| Out[55]= |
Show the number of equivalences between objects in the abstract quiver:
| In[56]:= |
| Out[56]= |
Show the list of equivalences between arrows in the abstract quiver:
| In[57]:= |
| Out[57]= |
Show the number of equivalences between arrows in the abstract quiver:
| In[58]:= |
| Out[58]= |
Show the list of reduced objects (modded out by all object equivalences) in the abstract quiver:
| In[59]:= |
| Out[59]= |
Show the number of reduced objects (modded out by all object equivalences) in the abstract quiver:
| In[60]:= |
| Out[60]= |
Show the association of reduced arrows (modded out by all object and arrow equivalences) in the abstract quiver:
| In[61]:= |
| Out[61]= |
Show the list of names of reduced arrows (modded out by all arrow equivalences) in the abstract quiver:
| In[62]:= |
| Out[62]= |
Show the list of directed edges corresponding to reduced arrows (modded out by all object and arrow equivalences) in the abstract quiver:
| In[63]:= |
| Out[63]= |
Show the number of reduced arrows (modded out by all object and arrow equivalences) in the abstract quiver:
| In[64]:= |
| Out[64]= |
Show the association of simple arrows (with all self-loops and multiedges removed) in the abstract quiver:
| In[65]:= |
| Out[65]= |
Show the list of names of simple arrows (with all self-loops and multiedges removed) in the abstract quiver:
| In[66]:= |
| Out[66]= |
Show the list of directed edges corresponding to simple arrows (with all self-loops and multiedges removed) in the abstract quiver:
| In[67]:= |
| Out[67]= |
Show the number of simple arrows (with all self-loops and multiedges removed) in the abstract quiver:
| In[68]:= |
| Out[68]= |
Show the association of reduced simple arrows (with all self-loops and multiedges removed, plus all object and arrow equivalences modded out) in the abstract quiver:
| In[69]:= |
| Out[69]= |
Show the list of names of reduced simple arrows (with all self-loops and multiedges removed, plus all object and arrow equivalences modded out) in the abstract quiver:
| In[70]:= |
| Out[70]= |
Show the list of directed edges corresponding to reduced simple arrows (with all self-loops and multiedges removed, plus all object and arrow equivalences modded out) in the abstract quiver:
| In[71]:= |
| Out[71]= |
Show the number of reduced simple arrows (with all self-loops and multiedges removed, plus all object and arrow equivalences modded out) in the abstract quiver:
| In[72]:= |
| Out[72]= |
Compute the dual quiver (obtained by swapping the source and target objects of each arrow):
| In[73]:= |
| Out[73]= |
Show the full directed graph with labels on the arrows of the abstract quiver:
| In[74]:= |
| Out[74]= | 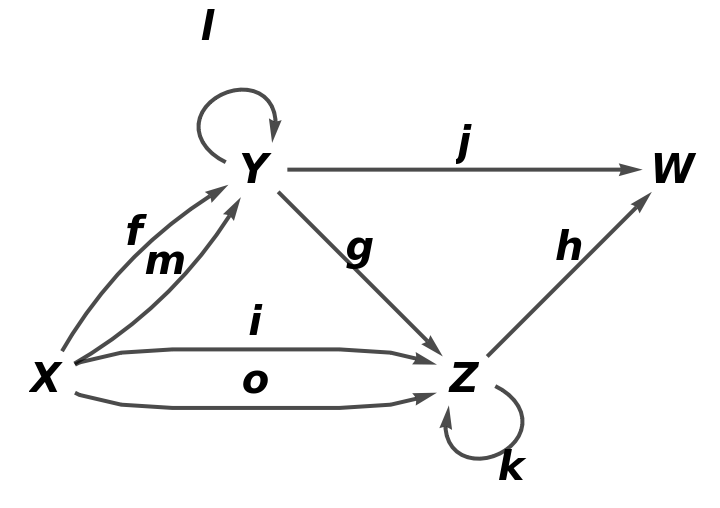 |
Show the full directed graph without labels on the arrows of the abstract quiver:
| In[75]:= |
| Out[75]= | 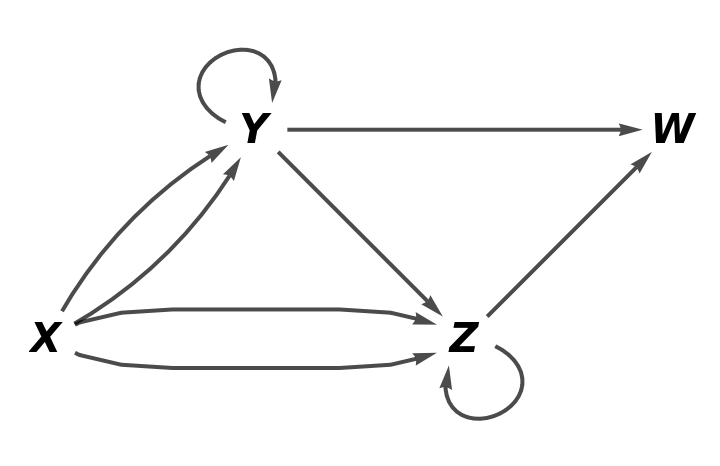 |
Show the reduced directed graph, with all equivalences between objects and arrows imposed and with labels on the arrows of the abstract quiver:
| In[76]:= |
| Out[76]= | 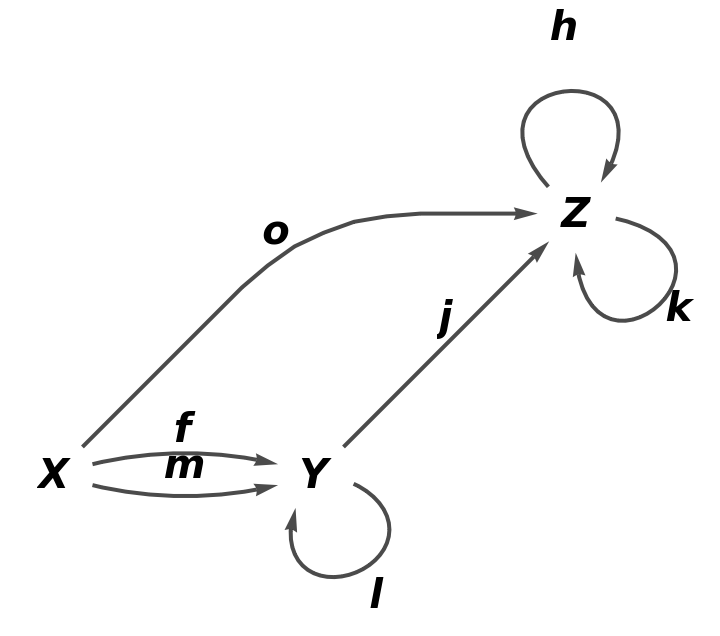 |
Show the reduced directed graph, with all equivalences between objects and arrows imposed and without labels on the arrows of the abstract quiver:
| In[77]:= |
| Out[77]= | 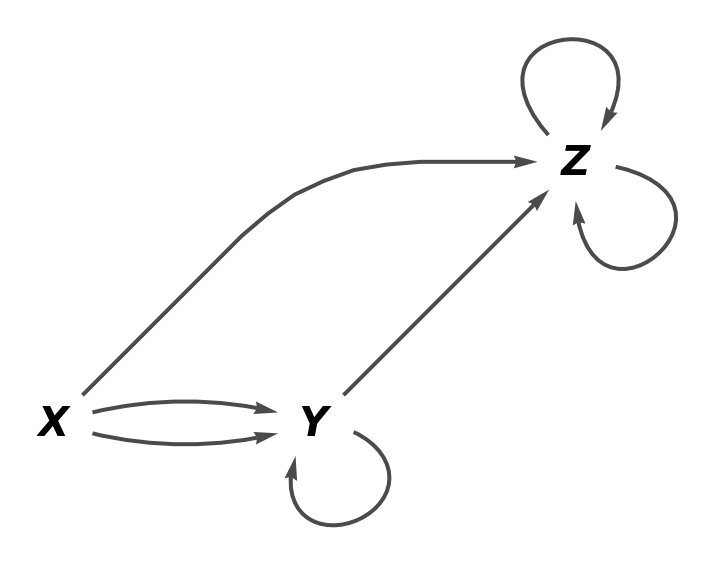 |
Show the simple directed graph, with all self-loops and multiedges removed and with labels on the arrows of the abstract quiver:
| In[78]:= |
| Out[78]= | 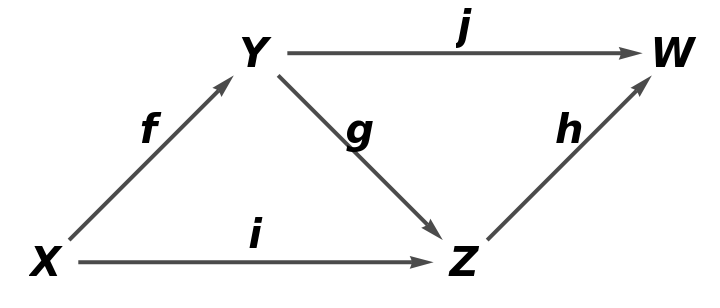 |
Show the simple directed graph, with all self-loops and multiedges removed and without labels on the arrows of the abstract quiver:
| In[79]:= |
| Out[79]= |  |
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all object and arrow equivalences modded out and with labels on the arrows of the abstract quiver:
| In[80]:= |
| Out[80]= | 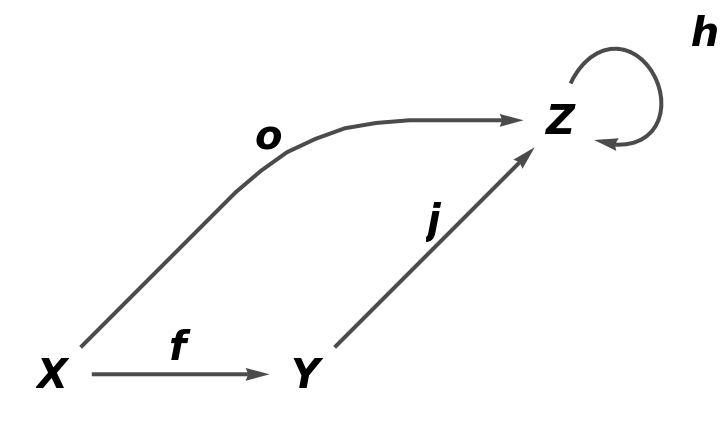 |
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all object and arrow equivalences modded out and without labels on the arrows of the abstract quiver:
| In[81]:= |
| Out[81]= | 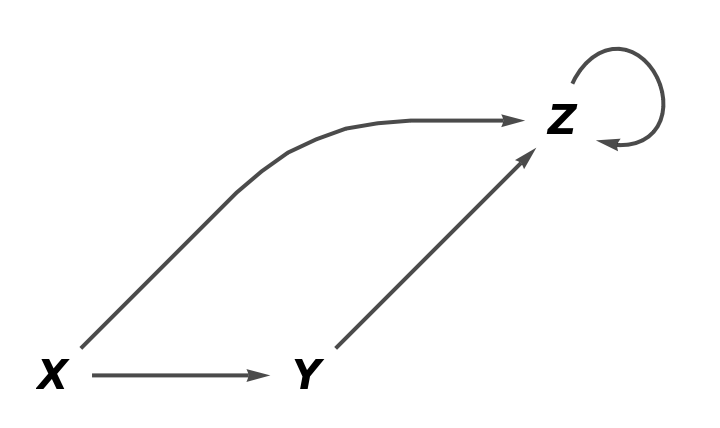 |
Show the explicit association form of the quiver:
| In[82]:= |
| Out[82]= | 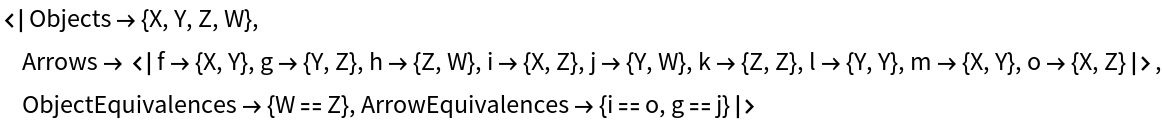 |
This work is licensed under a Creative Commons Attribution 4.0 International License