Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MolienSeries

Source Notebook

Compute the Molien series of a group

Contributed by: Tessa Wildsmith (with contributions from Wolfram Staff)

ResourceFunction["MolienSeries"][gr,n,deg]

computes the Molien series of the order n group gr to degree deg.

Details

A Molien series is a generating function attached to a linear representation ρ of a group G on a finite-dimensional vector space V. It counts the homogeneous polynomials of a given total degree d that are invariants for G. It is named after Theodor Molien.

Examples

Basic Examples (4) 

Molien series for the symmetric group:

In[1]:=
ResourceFunction["MolienSeries"][SymmetricGroup[3], 3, 3]
Out[1]=

For higher degrees:

In[2]:=
Table[ResourceFunction["MolienSeries"][SymmetricGroup[7], 7, d], {d, 7}] // Column
Out[2]=

Molien series for the alternating group:

In[3]:=
Table[ResourceFunction["MolienSeries"][AlternatingGroup[n], n, 10], {n, 7}] // Column
Out[3]=

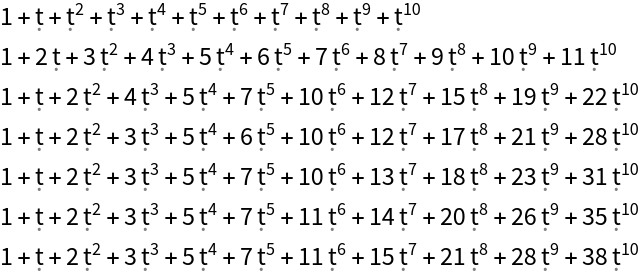
Molien series for a permutation group:

In[4]:=
ResourceFunction["MolienSeries"][ PermutationGroup[{Cycles[{{1, 3, 5, 7, 9}, {2, 4, 6, 8, 10}}], Cycles[{{1, 2, 9, 8}, {3, 6, 7, 4}, {5, 10}}]}], 10, 8]
Out[4]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 06 December 2021

Source Metadata

  • Citation:
    • Tessa Wildsmith, "A contribution to the computation of Galois groups", Thesis for: Master of Research, October 2019, DOI:10.13140/RG.2.2.18201.24161

Related Resources

License Information