Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the pair of points with the closest distance
ResourceFunction["ClosestPairOfPoints"][{p1,p2,p3,…}] finds the pair of points from pi that are closest to each other. | |
ResourceFunction["ClosestPairOfPoints"][{p1,p2,p3,…},"Association"] returns an Association with the indices of the points, the points and the distance. |
Given four input points, find the closest in 2D:
| In[1]:= |
| Out[2]= |
Visualize the closest pair:
| In[3]:= |
| Out[3]= | 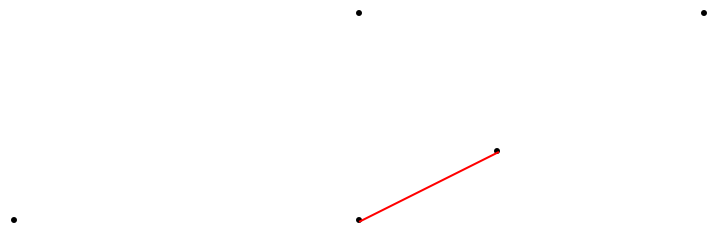 |
The function can also handle many points:
| In[4]:= |
| Out[5]= |
Visualize the closest pair:
| In[6]:= |
| Out[6]= |  |
Get the indices, the points, and the distance:
| In[7]:= |
| Out[8]= |
Find the closest points in 3D:
| In[9]:= | ![pts = RandomReal[{0, 1}, {100, 3}];
cpop = ResourceFunction["ClosestPairOfPoints"][pts];
Graphics3D[{Point[pts], Red, Point[cpop], Line[cpop]}]](https://www.wolframcloud.com/obj/resourcesystem/images/fa6/fa637d67-9a9e-48a1-995b-5daa027d0668/595ccf632db45e6e.png) |
| Out[11]= | 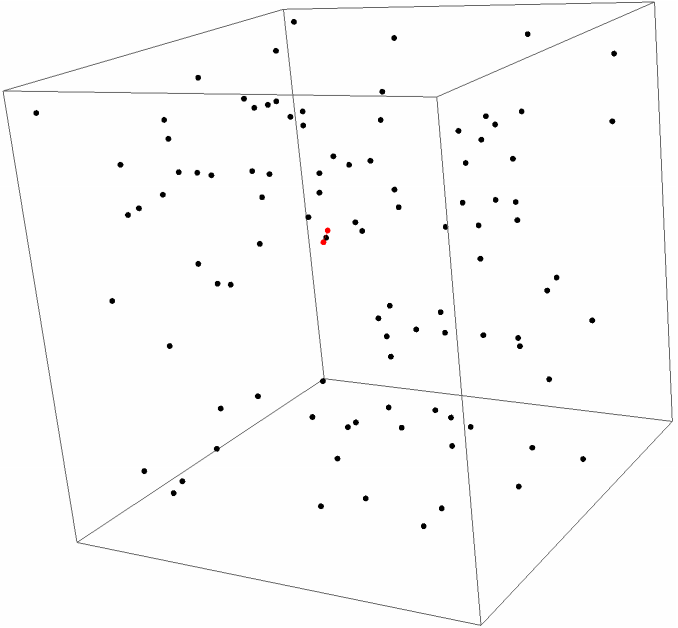 |
The function can also handle high-dimensional points:
| In[12]:= |
| Out[13]= |  |
The function can be naively implemented by checking all pairs:
| In[14]:= | ![pts = RandomReal[{0, 1}, {2000, 2}];
naive = MinimalBy[Subsets[pts, {2}], Apply[EuclideanDistance]][[1]];
faster = ResourceFunction["ClosestPairOfPoints"][pts];
Sort[naive] == Sort[faster]](https://www.wolframcloud.com/obj/resourcesystem/images/fa6/fa637d67-9a9e-48a1-995b-5daa027d0668/5d92695c68c4afea.png) |
| Out[17]= |
The difference is in the speed:
| In[18]:= | ![First /@ {AbsoluteTiming[
MinimalBy[Subsets[pts, {2}], Apply[EuclideanDistance]];], AbsoluteTiming[ResourceFunction["ClosestPairOfPoints"][pts];]}](https://www.wolframcloud.com/obj/resourcesystem/images/fa6/fa637d67-9a9e-48a1-995b-5daa027d0668/33b62ce002a78683.png) |
| Out[18]= |
Visualize the difference in speed:
| In[19]:= | ![timing = Table[
pts = RandomReal[{0, 1}, {n, 2}];
t1 = First@
AbsoluteTiming[
MinimalBy[Subsets[pts, {2}], Apply[EuclideanDistance]][[1]];];
t2 = First@
AbsoluteTiming[ResourceFunction["ClosestPairOfPoints"][pts];];
{{n, t1}, {n, t2}}
,
{n, DeleteDuplicates[Round[2^Range[1, 12, 1/2]]]}
];
ListLogLogPlot[Transpose@timing, PlotLegends -> SwatchLegend[{"Naive", "ClosestPairOfPoints"}], Frame -> True, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/fa6/fa637d67-9a9e-48a1-995b-5daa027d0668/38210ccb93ef87e4.png) |
| Out[20]= | 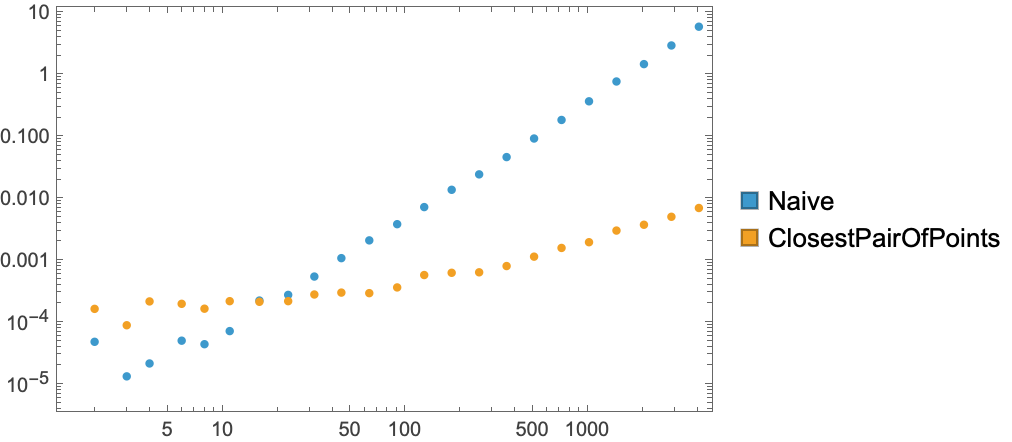 |
The dimension can exceed the number of points:
| In[21]:= |
| Out[22]= |
When no points are given a Failure object is returned:
| In[23]:= |
| Out[23]= |
Also a single point is not enough:
| In[24]:= |
| Out[24]= |
For 1D, the coordinate should be between braces:
| In[25]:= |
| Out[25]= |
Like this:
| In[26]:= |
| Out[26]= |
Check the method against a naive implementation:
| In[27]:= | ![And @@ Table[
pts = RandomReal[{0, 1}, {Round[10^RandomReal[{1, 2.5}]], RandomInteger[{1, 20}]}];
a = MinimalBy[Subsets[pts, {2}], Apply[EuclideanDistance]][[1]];
b = ResourceFunction["ClosestPairOfPoints"][pts];
a == b
,
{100}
]](https://www.wolframcloud.com/obj/resourcesystem/images/fa6/fa637d67-9a9e-48a1-995b-5daa027d0668/4931362b3ecb69e8.png) |
| Out[27]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License