Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return a discrete Dolph-Chebyshev window sequence
ResourceFunction["DiscreteDolphChebyshevWindow"][n] gives the discrete Dolph-Chebyshev window of length n. | |
ResourceFunction["DiscreteDolphChebyshevWindow"][n,α] gives the discrete window with spectral side lobe attenuation of -20α dB. |
A Dolph-Chebyshev window of length 21:
| In[1]:= |
| Out[1]= |  |
Plot the window:
| In[2]:= |
| Out[2]= | 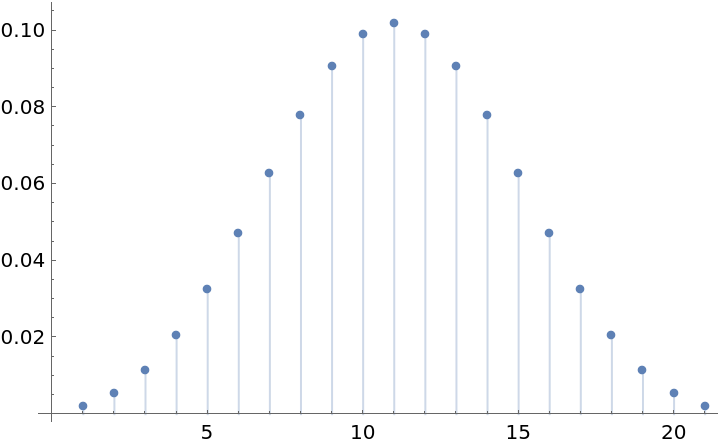 |
A Dolph-Chebyshev window with a specified parameter:
| In[3]:= |
| Out[3]= |  |
Create a lowpass FIR filter with cut-off frequency of ![]() and length 15:
and length 15:
| In[4]:= |
| Out[4]= |
Apply a Dolph-Chebyshev window to the filter to improve stop-band attenuation:
| In[5]:= |
Log-magnitude plot of the power spectra of the two filters:
| In[6]:= |
| Out[6]= | 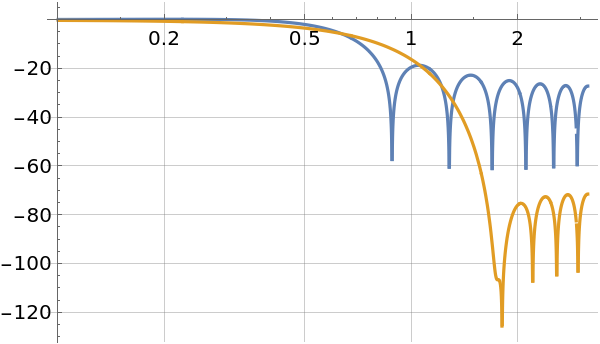 |
Use the Dolph-Chebyshev window to diminish the effect of signal partitioning when computing a spectrogram:
| In[7]:= | ![{Spectrogram[\!\(\*
TagBox[
DynamicModuleBox[{Audio`AudioObjects`audio$$ = HoldComplete[
Audio[CompressedData["
1:eJztm4k7ltv3xpuUiiKaSdFAURpMeZ+9Io2aNaeUNEpKNA9kqsgQRSFRhpIh
UuF99iIRKk6SoUgjColKSfTb+/tv/JzrOudcnVN4n2fvte57rfszxtp+xfYe
3bp1OyDL/rFiyyETB4ctRyx6819s27Jn+rQ9/H92Z3/PUuv2v7+KHt6H28tr
YE3ZQXB9v4reNCW4f9xn6lexQ3rgeV8a4TYbN8j5YGzMX3p04nqw8/4GbtEv
YcqYCNKR7Yf5Os9Qq9AR7dfeNF766jH5dfGecGCBJVW3kyVR74+CnVYalFuv
gJNLNVCn/AtGHq9B3SlD0NvBHAa1x0DrCgsYdylNaP4liqkml0ivst4wVGWB
9NDOc0isXuPhjQE4ffBdUqhRClsaamG32Ty4m/aNqqkcRO3zgzHuq5soL9SL
yzXH4z1Ta7Q0WUt3eHnC/Vvf4LXuAwiz6S2u00vFHi4VuCTbEqPfmZMh64bC
9Plu5J1VlOg8dDWx7LSHMsNwEN50hzwbW6wNa8VlJcW4efB5OnmFN1g8kEKs
rAVU5XpKjfWP0U0hDcL2j7Fk9VtDepj4obVuHp5avBorRk2B57cb4HFiNfzp
Lwsh9iZ49kUg7lgyEeHlejFpoJI4/HgHLZo8AWVmKAj7ll6G2rG14DIhEJZv
zaHJpAQNKisxov90LC6rJilvF8GuBc/IBZsDM58d20IWLF8N40+6wIc9FmSW
7wXcu+c3Gpy/h0aCm+DtkgTvrQrA0sQEIn8Y0XevX1Pf4YfEEyXaZOjoALrU
8Dxu2pGArko9MTLsKMj0+wNFWc9gbM/95JiMB8bo3MKIn1NQY22S5O83KuQ3
R9IXY6qporkdSSyOgKi6EvBfuAYGrzDCsIZ6dPYpxXe7W6jv2hlQVXgKytd0
A2ude5IFR3TIPKWp8CzSDI40OYvLPkWj06Zv2GNqACa5lBCN5iIIdykC5deq
MPFvPvUrHY02NhupU/4OYf/mWJpKTqPJQD/88nMeVZ4fCt9PdsCwhmQ41TNL
PBFzE7eopOHI9LH47Jcaaf7kRt5gfzrn30m6NUBK9CZFgIdDBjgr9wC5h67Y
lvUHbc7l4qbP8+i17GPQI/siPO0vB0UYIZ0W5CrUzu0FGpNkYaXlBRracgcX
TatG3+OrcEakCZzxrwNvyRNIan1B8gzG4qL3K9DjUxwdtVvDeEVOKNU8vwVz
GzbhNbmHgk9rMhz63gpXffxA0viWxkvysVvfTIQBsuikn0hSmz4SyyM9hV06
r8Xh3d6RVwrBkJAcChu89cnPszfwQvE/zNsRj+3Hfgk7Eq7Bzy9R4HupD+x4
0y6qKcWJNa9jyfnpN8jtxzU0NDgFZSW5eGRwJ42pOQNT8DfkLhVh+w81svbD
DizefgpdXYto6EM9yY/M7fTsbj10kh2F1wYkEp/tmaD+swYiBy6Hm8/mYVDY
e+z2UcSYtak0XEMRFm3WACOPyST8aozU//oH8qnQEzKKnWBdSS/qYSFi+Is/
KKz3xuHaX4j3xEz4cCMBdv37QKbf9qV+Pm5UoWQYUT0xnHT/KoeDNt5GvcUx
mNauRsu14+Cb1T+YMToaoqsG0fgbF1Eq44/zTpRQuwGxQpZyrph8pBfO0X9E
S8+x9zHnEcjFF4Lq0h/k7RVvtO35A+2NkrFi0w9xlvcyeH9iGWQO8yT6iX7G
w2gu8VxtA63tujBI5yld0P4UG0c3YLLhQvS6bA51I17BrbsJoKsVRBKPt9Jn
1z5Qp8bmDPe+3YU+xoNxnlUYpgW4YX7dRKLzPAdaWtshINkDvhU10ZtP7qJw
PgRdBz6gs6euIQcdPYRBT6Pp8OUCbRmsBXGfKCQWJILOBBliJJ+EWpp/cd3M
MHTuHEsKw89A4BonODTlChm6op+Y9sWHLDw3DW4uriaRO1RRpr0YN94rQeO5
tdQ4ywcKghtA1jEKzCYmCrsa9bDOQg0HfekUd454JT3QTR6dTc9g+MdZOH3M
Z5J+ugy847/C1hkmcKd4EUaPLMLtH8Iwt+UAfWmbQ5x6HSPbtUfS1FJFMXei
Ibw1vAO221gdm7mCpi14iqUb/6C60ylUONxMDhvGQEanBxi1ehPP4N5U97wM
mZnaQZ7XrCV7/M1QyaEIR4+6h/v6FYrJcimQN6MVEqovgPLqqXT/4QOYMGsu
9pc3pfdtEqWD1zRQ/VGbMGDVTzooYio0nKkGt2XlEHywjMib+OId//co6gah
oGMj2psOg9pv5UQz0UBapGctaCnpwzlpKJyMXww/Y3pgREk19gj5is1z9DFl
iTm8SsuCzTe9wDJCQvQ8fek9a22xvT6EJD3sLfyatB6V1bNRbtUFVL97hBiE
/Qdyiq0QONUetr34SjP9grDygDWGR8+lI7YYCdsOxdDZwzVR0XgPVWvbBD5F
VfDMJB209M8L7oPuYnxQIx4RPNFPz4D0nbkCnloMBvn6aGFyyk0B146FA5tc
4btaTzCtMkPXR5/x8bEKHLkth7b09oFA2VI4fcMTzFr/SMqimmhQN2t6qaci
aay6L2oO3oT6mxORLl6D/QYogGbRJ7BprodfqVrwX8Nc1B2ajCEe+3DHqr70
YvxEMmXceJq+sYbOf5slzcg/CpLaYqi0ugTbVf3owORidB/ThGGNlqgVWUsW
tbvD9156sP7LV4EcNRWWR8uAxZ0lEOxwiGypOYSvnn9GbQMp2lYrifLsPRbt
fg+zZJ2AyOtT4zIddJ6TS1s8kyRJtsPp+n3Lcfjfi6jRry/+frgalM81w4BZ
5bA27A4xkvHCBLXHGDFgLyp2TJdu+XCTbN3gLKl84UlPFfUid0xPw/w/CMfz
NoKfowrarPmMSZk1OOX5SIy9BOBreQ0M382DXS9TBfm7xqKeVgZxVBgC+xfK
So7neePsDW/xxtlgvLM2khxyKgat2E/Q3m0BWN1/Tf8s3IZWkt6Y4aMn9jEY
TJt89NFc4oB55Ufp6qOekGPxHWhvKTS9NTce1ZiI9UUlWPR0HR6y1yEXE3rD
5r4m5Hxoi7gv3ZrMrz0OT+9FQ9ohOZBv345GYism3C7BfomhdMYMDwjudg+y
xpvDdBPdDJ8moK+DTcjs3tkkxWkaTXcIxEGbCtFJewu+9ZkAmeu+wOnR1TCk
Vg6qZ+nhrTRv1Pykiq2H54skIUq0y1ZAS9DHGzuWSP7KhoBkbT24VwaD+b9k
mv+6CA/mVGBE7nT801ZALrobw51l8aRjYKo0wPgkWfhhG5yachZSqg6SC+/8
McbgD77ENLRc3ihZlXQLBn17BDunCqCopEoTVqTTc291JDu0VxGn6iBaNyIA
725NRS0XeayY6gRzFrTBqPJCODLJk/wbewrzX0dinOwEbFitIbE9OVh4ZpZH
n55so8P72ZA7G6Pg17ZX4BmwBVg/R4uCOkyd8hL1/f9Qz/oJ8DpvL3Tq1JCW
u4clHurryO1TpjDU1gISN6iK3Ztj8Cl+x7s7g7D+TBbJfVsAihFPYGGIKki3
pVKLYQPRzmokjYyKEWR0Uunhc2fRfFsQXlLaQ3u3X4FHOzoBDqfCoxEOotma
6zipPRl9rqmh1steJKduLokoXUm9NwbS+3FIbu2Jhoo3rDbMl4M53s7oN6YN
A6pzsWTOVjpn4V7oXnceKrR7QKW+jpT1D+FIyBAYaTkY5i72ppfz72LZ9w8o
q26FK6WGMDLqI7Qo5cPp86/Ivsih+FDXBMf/8qWBtnMkmZPv0A0GDtiwxA5l
enkL9ktSwPdYGww3C4Txjs/oQ89slOzKwN6VvTGnfwjx7sgkhxz6ifJefelA
5Qbi9uwqpFy9DvmTNpBhoZHoX/oPK80T0T87Sbj05TIsnRAOTW7dIdsxX3x4
IkSqZv6MGFxOI6/H1dFekx6ga/+n+PeXLJpMd4dEk1bwqJHCKDMjsrRpHUqy
9+KDIek0tNTH2N/Rh56Eefh0zCQc6BtD5jk/hK3NX6BdZj0oLySo8rUK1drS
Mdg6nc480QuqJimCaXKdsLC8l6hk10r0En1haYUL9O37nzjxuxRXn/iLn876
YsX8UpLyOg0MVtyE6Pxqcm7cYXq/ZRadO34jmbLEgCidU0S5o8n4NCsep3w3
o+OuxkLDyU5Qt4yBA95vxX5HfXB00ll87ptLL4sHBJ1MDTrsyBB0/FNBrVfK
wkKVPPAoeQG7H/aEuXZn0Cv+G44fcgfHWSnSCYamkKEE8HXnZqL0WV6i6vCW
hJx2AvGjAPcl2VRjWSGuXdaE6gdX4GxXE9h9pwSyFOKg9tYVcolU0Z0elLaf
XS7oXTUWTtxTRaMHN/Cgnhdmb5cjuamPYDH+hf7rz8KBK6/p+KZ49L94EQ+P
SqYP7aYStf/8M24o5lOtPEtakKINzy0ewfOMVBCWTCSjqm+jus0f9CkKw50r
ehIbFRfod3sbKF87RzLOW0qvzE0gCzXNwG7+T2JrpoL/9S9FO+0KzMtqo7Kj
zsGm/XXwIPQ6/BpfIVxcNQHHLpJHS6uroqJqnVS733C02ueHs90X462sN6RC
rhxC+zXD16T5YKVvioo983Gh/2UMbTlEh9jfJieH65Kzq9fS3JBVYuMNAO22
+/Dj9gXoP2Ya1XQoQFmzP3i33AUV+lUR1cpwsN7vDP2s3Un92BwxwnwR8fo4
EFqfHSEz1edhlUYJmrhkYNgMOapimgjN/t+h1/ML4C9VoPvebMWkdD3M6lSj
wT9HiwozZPDPNHuclySD87ymQFjBOwiQr4TEsZ+J3ORzeCWiCutvB6KCf5CY
4tYXBrankA/qh8So6E2Cn44JXLW/Ad+a1sFHtzba3a8aTdS/4cZ2CcbNnAW1
nemwKdUD/OMFUvvPjvbM65T0K0sn1estBDufzdholI9eBsFoPXotUelXCI5D
foKwwQG2zX9Fn2f7YueSlZhtO4Me/DhHcrkjn47+aIiZkz1psf1mmJ72Dhrk
EQavKxM+JSbiRpUvON7XA+NKh5IVOqagMrIXzDQ2Fhx65guNl6aBtr8XzB45
AKL+M0Fl3XocfrQSHWaU0jFeZyBp/X8w8oQbDJwGwk2VYurQOoR9TzPyIi1J
zFXfiVqe9/CS6lbMceoLCWkfwT6iAWj4FOiz3xjn5t3CTqdtGOjch8bV/RTM
7fbRh7d74J6/emK3bs7gNL8cUl+EwGHzE7R4WxHeXNCI33pb4Z6hL0hq6DEQ
2sZBofSR0P/4NSHcYghoDbOCg0vOk3KDw+j4uQGrbDKx2itA3DA0AfapvQHD
Qw5QoDiMyh5VxelZkfRP5QHhHhlPb2RuQq2cMPz7WQm7iyvg2IgWyD/2CrxP
ZpFsTXd8kJmJCue342jPAqm3tzfJumMnLrGIpAPkOwQL9o703XNhqNIueKQz
GBv21eK0KzVo3TAaEx5NB9bPwSXHGFYF3BbmWDumP79WTSocx4GtTadk4yMf
PNr2EU95hOHr2X7E3LEQYn6/h5UDFkKJ+WN6ZuVKfFnVQFcvjpfaT55GZ56c
i1XyLnhxjy/91d8T9vj/BAM/hJBVo4SXdrewhhZhrPJq7NddkUgWNJC+ss3C
4hHq9OX5PeR7gBvskUmAD5OGgkL7FnSxb8VXGqV4IjCO2rNnLfcvAVTPmoKp
4wDJeq3e9NB2D1L2qorU7dWinmbByP1533e2OCJcDcbfqIVJ49+A+TRFeDxJ
C0c6umFBlQLuHDVJdJnXIVadUMeDu+ZgU7mZ9ObGUPim2QQbNoSBrtU1Gj/p
CX6bU4qLC6ejWuE90nfYRCCnvImX8mwxSM2bvGp0hLwCP+jMOk9yy/3Q/WI7
fr0mRcnHnAy7xBuQMg7BdYshfN3QgzZMvkwlu2KFg26nyEq9EOpzPRiPa0rR
789Q1DCyhwCV3xBxrgim9b1IUjUcMHNeCHL/8TjAeaZ+WZA01aaRNhr0w9hZ
a4mJayyk+1aD7nVbOOmiiU4LPuHU7S+wKLsbvowZCcknNoLCuQKi9jHZeLe2
C0n3sYDjxtbg222OtDIoFk+nt2Lh1hAs2ZdATp3NgZEbHsO6KBU4FBJBfVP/
0OOvEkXT+W+FDX6Z9Pc5P3QNvYopwWdoxqrLoPm+E/Yl3IdhzQXSCdWheNz9
Nk4sGI4G3coF/WEyZKSWL52gcYsu2pBFFJfGwfv+ecD6B5yaeBSnDP2FmkW5
+KbyODXM3Qx9XrhD4Jwm0v+Oa0blZV3S8lATtj9WB9ne7rTZ8D7KWtbhi1M7
sdVvCpRtegv/ueTCgZpq8nNOf6xdNAWNZLbTsUdzJbcWPqILjFzYZz+GE/qO
E8xNU6DqcjsMuR8EZb/TaPEFEY133kONll44I9eTGE4PI8OPF4oriyZQtXs/
SZtBFDhtvQWzFjoT/3XXsMP2HxqWJuEuw7WCfJ8A+DU4GCqdfhK5TyGi8Vw9
oSSnmTx+WkS8RtXR7uul6BH4HBe+GIRrzVxg4MbvED9ECsduLCP23RehnLgR
FXZep7HO/kZa+2KpQclaPLLNEE99ukpadR8B8f0KNdHWMMh3Bs7/Uo7S6PvY
pE7pN+EbKU7qIE12W4TSrbPEW/U9IWZpEAySnoGsxQGita4Uf6V34J39FzDS
+SGZvzIFZl2/DmPHviIDGlZQ7fwWUXOSPzmycA3R2j0Y3ckDHNjnLn45tpv2
xihQ1O2AxcaxYFkWJuoYeqK+8mkcIdynqafGCNEV1rRwtyZ67v9GFfb2gVne
T+B7QjlkSuRhSz83lPxoQEXvRPx5eDzVbZ8O49fpwH8LdMlLcYIk9/tv0qTj
CndrF0LktDRqZVyEw1VbcOjy9ahqZgA5bYUwUTYGLlWEkrMJj+i0VZfpqKcf
hAUznIXEo+Nwf34cRmb5494BFcKKmdmgNaIDKu96wcywx7TX+2g0neeLz/EW
jSiSJ3vfXBLHRdRTI9OTtCVgCrzdmg/tThkgPltKjmy7iV+m/8YEmauoPClX
aFM+AHmuq6Dc4QDZu8vbuCLlKdkUtQr6NMqAk9MIfJlcjm5Lq/BNkwxOX+QO
feo/gL5VBDTf6RTKPg3DM/KtdKNmjfTx7LfSqr1jsdY2GGumrMeo9S9IuE45
+HZnnoYuhQnOBjj1+kMc9SYQdckROkUIJA/DC4RdO73o0lB/0XnLXDi8m0Ju
aTDUVyrQBCEPDaVt2Bnlimub88iZNcFwZMIBKM4/TPzuuoj19WdIXrcxsHKu
D+n5cz4+cCjH2dGZOMF1Kj0xNQ7s3b9B0pYLcMPtg7jMaCW+zhuLk3NaxXh7
K/FtqhK29XXGnBYFHFGkDaHXPsBeh2qwW/eHHPnuhjVrytH8kT+e2PBAvPfv
J4lN8iGp8h9FDWGZMDfYHF7XxsEc7e3gmttANT68wdxZzRivPxt7qujB6F53
IcrGBWT/GhNjSmj13RKB9XMyLyFQ2DB5O477W4hHf4ShzyU98lf1CQgJ30G+
0hEWTsmltmWeaBc0B03s1Gjt/MvS2Nx6Gp6wAP2VL1MvrS1QbfwJFl/MBvG6
AlkhH4c5M2tw2Sl3rD3zQ/CbMA2CFD6R0Z9/Gd8pfi+0wywovBYAFWbDwWgs
wfeTG/D+yGq8YV9DtZpOg+G6ApD/7gxLVA4Jq8en0gyNINHvxFHiY3xDtDi0
H81sRdxRthdz9/aAOuEDdNY0/M+fD/8zBb1NrqPivXU453MPeuTwFeF0eyg9
azkIx/05K44yPA1jllTByREREBS6jurkPMEDMvV4dv9mvDwCiewQWyjbNQR+
61wU3ANfCX38x4PyHnsQw8PJ48JD+PZSExbMe4QzXCrFVZ9joadDBTSp20Pv
kb/FNj15fLP+BF0686mQNE+Xntxri/Oso3Di51HYOWoJtAgtMGhNJTTe+Y9k
7ziJX5TT8a/5JlSzUhIjnluRjU296W5/kcoL9cLex+egKucpDDB0hB5u8tg0
/hOukK1BnyPjcEwfTdjp6Qc1MlNg5tMwYfb8ScK+/O5wrW0GhCfZCHqWftiq
/xlnLI1Eh9JjRHZsATS9qYYtOxfCvrMp9PPs2eix4SnN1b5ovOXgIqrRuAo7
vpzBOQMj6SxTD/Cy/gVu+Q8h8s0lYa30BlYsK8CjV5bjDOtG4bnXExIbLxFG
ti2i+y8cIJ2W5+CGWiqs+zYGGm0t8VzqT4wwKMP7KWl8fgV9HsSA1nQjGHjR
V7JjYKi46k0cOb20jYS/VqXuySFoXFiB2ZsPYs3aoXDV5yPsyawEhVplSJip
issUDuNE6IlHn/YQKxU0adX76bghciUeKlAV+y0JA6/AFtgRHgFFQeep47Rc
NLAqxt1q0zF+23UC14eB2n+ryL2CK+JrMYjMvusC3guDYUDYNQKHfHG7+19U
0UG0VRonfnC9Coq90sC4eBrMLnwhyvbfT80VRxHP6ovknUYY5f6jKukhGjqp
49yMnWDg3gpXyorgft9I8kFxG049GIAlQ5TwWntSxvovF8Qzqn3x0beheLP7
QuJsyu6i9UdYYu8Ex6LVUM7uHQ6f9hxJRE8MDBoIZr/NQeFFPFGc/j5D2zWQ
rNe3AdW+++Fsk6uk8VUs+i1qwz+q4Wi5JITca0LIvfMQGlpHwIN4HzptRRkV
4y9LdxcPIHkeBXSVJAgDEqNwfGAI7bEhCP41dkKMVxqArLzEyuwSsv6Buw2V
UHlknDBH5qzws8ddujszkw6LziKa/yVC/5/PYHToaFj90AEv3/iBlWtyccW8
c3S2qQW0Kx4Dr0/lRFm55oF3vQ2ZlzwTmq11QdA4QmFWGobsaMC/XvtRa+J4
0Hn4GnI9smH/rw9k0dpOWmaiinm6E6lcupqQPbCUXh5xFhe1uqGtx2TJ9RfJ
8GJRB3h+uAKCXzT1tr6PR2Tv4ISlPfDd590kbvEBcrpSmwYumk/3fOwg9xfF
QU57EkxcGkAuMD2tG9CJpr2SUX9+jGRCX29oS/eDV041xDVquzhkQoWQPaI/
DBFriOP9GpqtkYm5xaWoeUEFcyVH4azSN7CtTofBv7eR/awG+WxahPtdvajO
lovpzWZZ9LPqblTPn4P7R10kSYdzoOxJMzyp2w3foydi/cUX2NyYgkb+mdRj
bDnZ8r6cpNffzDg32lXc2NgfUuKuwkxvX3h1dIKoLp+B+706sUb+IhrUJRDD
y7eh5koY/Cf/gtx7PIXmHV4oiip3yZi1R8gsn2FoHSPi36Hp6Kh/hvYLiARj
x3Y4kxEL7fnGonz+KcQ9jnjTK5rKzUyRyA73o8GzZ+LtRz0x+LUMvAkoBCvD
KpjqPQSeNJ7ESa/qsOpKPI6wNqIN1ePg6dqR0FbVLgRVD5aMGikLX229YMmf
NXBfJYFeEIswx+0H7sncgpdqtEHjdx4cCY2Egwlh5MCb29R13k7630tdMvFi
jHDPTRvTfJLx3bRgZP1c0N+SBT96d8ANPA8PGlLojpvheD3qDC7+EUFvVZcL
/oIitZnWBy2f+1GL+1NhnFIh7PiRCWrHnciMG1FYFvwTO1+F4cCXZwTt6q0w
sc4MTvdZSv6OD5cYj/lCbFq3w6NDirDs31A0anqFfVXe4bucARi1zBneyFbD
rYyrEPdsIPGI7YcnVJ/TjF2iJD/xofST5hTmJ6/hm4rtuLo9lwyvKQM7vx+g
s2o1hKdro3M3KX5+4os7nhyi3J8viCqVdBjF0e5TRfHEpkVQd+YRRFRdhUFa
VaJKYg4uz/2Ne9Tc8aNJKumd5AftxTaQ08OGvB7aW3TsFUfmjZ0G9S7XyOX+
C3G7ZSVGnslB2cer6YDqaFBSbARbP3+4P/CmqBBohgOclPBRcKw41uWs2O3m
GFTecAZ37VTBz/u14Gy/T/Dm2HtwcZaBF9qnUOlBMZ485IPyi0rE6mMVZOCy
FWTEYE3aMdRAOLlkFZwYnQJ5axxAa1w1q1dVqPSzGfOb5uPKDi2YV3gbthw4
BFoeBuTRTkWqBDNI1KQ/RMHwkZDUzxZnbStB6nEdj5BBZEDlYygsb4anCQfh
QEgy7Yg4hWar9DE7pQ9deXuWeMqqN0barcclNI7KsJ6fv6oOMl48hm+r9cii
KdGo/fMdjpN3w8kzRSFlujpYmGcR4zO9xbJhv4RrixZDzzMh4HthLIx+Y4Ry
WQ1YsvEdnu/ZSt33HQU52UfwfsBR2H7kgjChNJhKXsZosn8T9muR/Xdk/x/Z
7+O/n7A/B+zP86/Dvx6yr4vs6yP7PiL7fgL7vpR9f/5ziOznAfZzAfv5+M9J
2c+L7OdG9vPzz0HY5wH2uYB9PoF9TsI+L7DPzT8/Yc8B2fNA9lz486HsOQF7
XsCeG7DnJ7LnyJ8nZc+VsOdL2XNG9rz5c+fPH9h7+N/+g70Xwt4PsveE7H0h
e28ie3/8PVL2Pil7rwJ7v8DeM3/f/L0je//IzgE/D/xcADsfwM4JsPMisHMj
sPMD7Bzx8ySwc4XsfCE7Z/y8EXbugJ0/YOeQn0fKziWy80nZORXYeaXs3CI7
v/wcU3aegZ1rYOebn3OBnXdk5x7Z+Ud2DwR2H/i9kLL7Qdk9Iey+ALs3/P7w
e4TsPiG7V/x+UXbPgN03YPcO2P2TsHsoZfeR30t+Pym7p8juK7+3/P4Cu8fA
7jO/1/x+I7vnyO47Zfdeyu4/ZXUAWT3gdUFk9QFYnQBWL3jdoKx+IKsjyOoJ
ryuE1RdgdYaweiOyukNY/QFWh3g9IqwuIatPyOoUr1ciq1vA6hewOgasnoms
rvH6xuscYfWOsrqHrP7xOsjrIbC6CKw+8jpJWL1EVjeR1U9kdVTK6qnI6iqy
+srrLGH1Fljd5fWX12Fk9RhZXeb1mddpYPUaWN0mrH5LWR0nrJ4Dq+u8vgus
ziOr98jqPq//hPUBYP0AWF8A1h8o6xO8XwisbxDWPyjrI8j6Ce8rlPUXYH0G
WL/hfUdg/QdZH0LWj5D1JYH1J2PWp3i/oqxvEda/gPUx3s94X0PW35D1Od7v
KOt7wPofsD5IWD+cyfoiYf0RWJ/k/ZKyvomsf/I+yvspsL4KrL8C67OE9VvK
+i6y/iuyPiywfkxZX2Ye35v3aSnr18D6NrD+zfs4Zf0cWV9H1t95n+f9nvd9
yvo/ZToAmB4Apgu4PiBMJyDTC8h0A9cPUqYjgOkJYLqCMH0hMp1BmN4ApjsI
0x+U6RBkeoTrEq5PgOkUYHqF6xbC9AsyHYNMz1CmawyZvqFM5yDTO1z3EKZ/
gOkgroe4LkKmj5DpJGR6iesmwvQTYTpKZHpKZLoKuD9nOovrLSnTXcj0FzId
xvUYYboMmD4DptMI02tct0mYfiNMxxGm55DpOmT6jus8yvQeMN0HTP9xHShl
ehCZLkSmDynTicZML1KmG7l+5DoSmJ4Epiu5vuQ6E5neRKY7uf6kTIcC06PA
dKnA9Kkx06nA9Cow3cr1K2U6Fpme5bqW61tgOpfVqzBgupfrX66DKdPDhOli
geljZDoZmV7mullg+hmYjgamp7mupkxfI9PZyPQ2ZbpbYPqbMh3O9ThluhyY
Pgem07leJ0y3I9PvyHQ81/MC0/XA9D0wnU+Y3heY7gem/7kP4H6A3cFKZP6A
+wTuF4D5BmD+AZiP4H6CMl9Bmb8QmM+QMr+BzHcg358zH0KYHwHmS7g/4T4F
mV9B5luQ+RfKfAz3MyLzNZT5G5H5HGB+B5jv4f5HZD4ImR9C5ou4PyLMJwHz
S8B8E2H+KYP5KML8FPdVhPkrZD4Lmd/ivosy/wXMhwHzY9yXicyfIfNpyPya
yHybyPwbMh/H/Rz3dcD8HTCfx/0e933I/B8yH4g8f8V8IfeHhPlEyvyiwHwj
MP8IzEdyP0mZr0TmL7nP5H4TmO8E5j+B+VDC/KjIfClh/pT7VIH5VWS+FZl/
5T5WYH4WmK8F5m+5z6XM7yLzvcj8r8h8sMj8MDJfzP0xZT4ZmF8G5pu5fybM
RyPz08h8NffXAvPZwPw2Yb5bZP6bMB8OzI9zX879OTKfjsyvc9/O/TswHw/M
zwPz9QLz99znc79PmO8Xmf9Hw3UFqNV0ms8FyP2R1fB+cgOfF/C5ARZeC8B2
mIV3it+Loz//yghS+ET9Jkzj8wZx2Sl3yJlZAyvk4/g8gi6+mI3Vxp/Qi/V8
f+XLJDxhAcTm1pPa+ZclJnZqxC5oDtiWefI5B5GvdEQh4Tv+VX3C5yD06I8w
GPe3EDZM3g7zEgJFvv+ovlsiGlNCZP8a0ygbFxzd6y6fr/A5C+TOagaND2/4
/IXM0d6Or2vjcG6wOWoIy8RU+Y9CbJIPvffvJz2x4YFg/sgfataUw5Hvbny+
Q/c6VGPotQ987sPnP9DW1xnepipBvL2VMDmnVXidNxaWGa3kcyMhacsFtHf/
hiemxvG5EpkdnQkPHMqh58/5fO5E87qNwfr6M9TvrotQnH+YHplwAM+sCebz
KtoZ5QqG0jZIEPL4PIvklgbj4d0UnbfMxaWh/nzuxedf4hQhkOqSI2TUm0CY
ev0hn5PxeRn6dv+O4TrlfI5Ga6ash1rbYKjaOxYez34r2ahZIzkj30rKPg3j
czhR3yoC+9R/4PM5PqcDt6VV8DK5nM/v+BwPN0WtwoqUp3TvLu+McocDNM91
FbYpH+DzPzFB5ip8mf4bjmy7yeeDtN0pA99uzceWgCloZHqSjIuo5/NEIaJI
nj7HW8R0ni/0eh/N546k8q4Xao3owBUzs/lcUozM8of9+XGQeHQcLJjhLI56
+kGctuoyn2eSSxWhdKJsDOa0FfJ5J597wnDVFrAyLuLzUHK3lt1tHVfM/f6b
vhQnSP9boEvHr9NB3fbpfJ5KFL0TQfKjgc9Z+bwVvyeU4yzvJ6iwtw+fx5LC
3ZoQXWFNUk+NEUcI94m+8mnQMfTkc1xhsXEsKup2/M+ffzm2mwzscxfcyQPQ
2j0YjixcQzUn+fO5sDCgYQUZO/YVnXX9Os5fmcLnx/TO/gvwK70DrHWlfL4s
DJKewZilQXirvieWbp0lNNltEYuTOvhcmjapUyKNvg/zv5TzuTWfXyPx/Yqt
uo/4XJse2WYIBiVrQWtfLIl19k9T2HmdyIkbwb77Ij4Xp/FDpDhw43c+L+dz
c/AIfA7d10vBa1Qdn6vTkpxmajxXT5T7FCJUOv2kvwYHo3yfAD6PFw1Lk6DD
9h/4r7vG5/XUaestbDOIQrV7P+nKogl8ri8YTg+jM3I9qUZLLzDeeQ+KL4h8
D0CG3A/CqsvtaG6awvcE4suYY7DAyAVuLXxExh7NlRrJbCe1i6bAzzn9+Z6B
/ueSi2Wb3vL9A99DgKxlHTQb3uf7CbL9sTq2PNTEysu6tP8dV+PAOU20zwt3
NMzdzPcbRLMoF6YM/cX3Hnz/ge/756Hi0jhctCGL70f4noToD5OhBt3KxYkF
w+G4+22YUB3K9yqSfQn3UfN9J2asusz3LsQ19Cr8PucHG/wyien8t+LxV4mC
b+ofcigkgqyLUsGRGx7jqbM5fJ9DC7eGwOn0VqgMiuX7HslxY2tM97HA3dou
VO1jcobCuQKafGIj3xPxfRFM3f4CnBZ84nskvk/CdN9qNHGN5Xsmvm+CVJtG
ol8WJHkc4JweuUMVMueFQKqGA99T0YhzRRig8pvvr/geC45rSsHnejCs1Ash
B91O8X2X2DD5Mvm6oQdx3WKIKeMQ7RJv8P2Y8ddrUnC/2A655f/bn9G8Aj98
1eiIQWre1Et5tkBOedO+wybyvRtdXDgdvs0phfhJT/hejmzYEIbfNJvw5sZQ
vreTHNw1B6pOqIPLvA5h56hJQkGVAox0dOP7Pr73w0nj3+D4G7V8H8j3gpBM
SsDTLBjq9mrxvSHfH9L1Wr2JqeMAqepZU5T7l4D23Zz5vpG80igFF/tWvofk
+0jcI5OA3wPc8OX5PXTxCHW+txQlCxpov+6KNFZ5NdTQInhpd4vvOUUDP8Q9
/j/xV39PvgclVfIuMPPkXLCfPI2sXhwveVnVQM6sXMn3p2TlgIUY8/s9mjsW
8v0qPeURBkfbPsLGRz58/yqtcByHz69V0znWjjNXBdwWXXKM/5e/Sng0ne9v
YdqVGmjYV8v3uny/i/ruuWiR6oED5Dv4/pfvgQVvb2862rNAonB+OzzIzIRs
TXe+N6b5x17hsREtfJ/M98qgxfT0jcxNcI+MJ38qD4jTsyKJ7FFVvo8mhocc
cJ/aG9wwNIHvq4UqG6bVPzdAucFhvs+mWsOsMNxiCPY/fk0slD4ShbZxmBp6
jO/B6bfeVnBzQSMUbyvie3KS+iIEneaXYzf2rPf81RMe3u4B5nb7SFzdTzHQ
uQ/pdNoGc/Nu8f0738OjfUQDJqR95Pt5vqcHLc97kKu+E16kJQkHP5rxfT65
qVJMBk4DceQJN0xa/x+O8TrD9/9k+NFK5ifreS6A5wNQ298LGy9NQ4ee+eJM
Y2NRZWQvXKFjynMFdLyvB2xU+QKfEhN57kBskEecnvYOi+0381wCGf3REC53
5JODH+dIs21nkM4lK+F5ti/PMxBhgwM6DvmJKv0Ked6BehkEQ6NRPtj5bIbq
9RZiv7J0no+Q1v6zI/7xAt3E3lFtZzrPUfA8BZiof4PuftU8Z0G+Na3Dq/Y3
0E/HBKOiN4kf1A8JA9tTaIpbX57TEOpvB8KViCqQm3yO5zhogHwlhhW84/kO
nvOAP9PsQWGGDAT/HC1kdaqRpHQ92PdmK8+HkF7PL2Cz/3dUMU3k+RFi4pIB
VRolMFN9Hs+XUK+PAzHCfBGtH5sj9LN2p9b7nVG1MpznUujdcheQNfsDmg4F
PLdCfty+gNpt97HxBmBuyCrh7Oq1POfC8y40tOUQWeh/GRR75vM8DM/FYGi/
ZqyQK+d5GTrbfTFY7fMD7X7DQVG1TmJpdVUYu0geLq6awPM24oPQ67hpfx3K
jjrH8zjETrsC/utfCrZmKjyvQxdqmuGVuQk047ylRPnaOdrv9ja0UXHhOR8+
bwd1mz8wqvo2zwHR5xmp+NziERakaKNWniW5oZjPc0PGD+2m0sOjkon/xYsw
vime54tI//VncTH+xdzURzx/RA/qeYHRgxtw4p4q6F01FtvPLhd3elCeWyK1
t67QLIU43H2nhOeaeL4J1i5rAo1lhTz3RMSPAoacdkJVh7dU6bO89OvOzTRD
CXCCoSnPTZHxQ+6AV/w3nqfiuSr0KHmBC1Xy0HqlLM9dEb4/18nUIJfFA+Jz
31wyOuks9Dvqw/NagrplDDac7MRxV2N5nos8zYoHuaPJoHROEaYsMeC5L57/
4jkwEp1fTQ1W3MSU12k8J0Y/nfWF1Sf+wsTvUp4jE5ZWuKBeoi8q2bXSheW9
BNPkOrFqkiLOPNGL59CIWls6qHyt4vk0nlPDrc1fcJ7zQ55fo0/HTIKTMA/8
HX1IaKlPxoMh6USSvReWNq3j+TfqUSPFRJNWnovj+Thw7f8Uek16AK/H1fH8
HFUzf0YfngiRZDvmC01u3XHphHC89OUyz92JleaJ4F/6D4aFRvJcHk25eh3d
nl3FgcoNVN6rL8/vCd4dmTSnfwjtXdkbJLsy4KFnNs/7keFmgeh7rA3tl6Tw
PKDYsMQONhg4QObkOyTQdo50/C9f8lDXBPZFDuV5QtqilI8joz7ynCHPG0LZ
9w9wOf8uzyGSkZaD8UjIkP/l2yv1dSQV2j2we915nLNwL88xkoDqXPAb08bz
jTzniBVvsvDWnmi8H4c8B8nzkDwXSbVe9qI+19RgUnsymK25zvOTAhxOxUc7
OrF3+xWeryTm24Lg8LmzIKOTSiKjYkQ7q5HEYthAnsskC0NUUTHiCea+LeC5
TXp3ZxA8xe/QvTmG5zqFobYWePuUKXqor6Mtdw9LO3Vq6Ou8vehZP4HnQknq
lJdgUVDH86I8N4q/tr3COxujcHg/G54rJc/M8ojtycFiw2oNaZzsBMh/HQn/
xp7ieVQ6qrwQ5yxo4zlVnleFu1tToW5EADhVB5Ed2qt4rlWasCKdKCqpkp1T
BRz07RGuSrrFc7DSl5gGMQZ/4MI7f56TpaemnMWFH7ZhgPFJ2jEwVXJnWTy9
6G7M87U0Inc6HMypYN+7iOdviXtlMErW1uNf2RCez5Vagj7YZSsASYgSWg/P
FzQ/qcKtNG+e6+X5Xjw9uhoz133huV+e/4VBmwoh3SEQUpym8XwwzwlTnyYg
0010jbPGm2Nwt3s4Y4YHzxWThNslYCS28rwxzx3j03vROL/2OO5Lt6bnQ1uE
zX1N6MWE3jyvTIueroP6ohIY1ZjI88wZtLcUcyy+4+qjnjzvTMwlDtDkow99
DAaTDB89wUrSG/4s3MZz0qS92wLUiv2Eh5yKeY6a8vzV7A1v4XieN89ZSx0V
hqCeVgaVv2ss7HqZKhq+m4e+ltd4PpvntCEpswZs1nzm+W2e48b5fxDvmJ7G
U0W9aOULT5735rlvqtgxXRIxYC8kqD0GIxkvng+nA2aVo/K5Zp4b5/lxGP73
IqzftxySbIeTFs8kqfOcXGJcpsNz52SWrBMW7X6P8nIpPJcuaBtI4dXzz7Cl
5hDPrVOLO0twebQMkqOm4vovX0Xuzxe1u/O8Ow1rtAT3MU0wMLmY5+FJpdUl
lNQWY0b+UZz/NkuSvrGG5+fJxfiJdMeqviTEYx/oDk3mOXuet0eb5nrULPrE
c/g8jw/6mxNBc/AmaKy6L1zqqchz+6QsqomYtf6Rnr7hiYGypdjS24fn/Mnj
YxXg+ugzz/9zDgAPbHJFXDsWJ6fcFOXro8WnFoOx78wVnB+gRwRPiA9qBPdB
dzlfID4zSUe+/1Br28T5AzJ7uCZsOxRDRmwxEsOj55LKA9aQ6RfEuQUSONUe
5RRb0SDsP841ULlVF0BZPRt+TVoPSQ97c/6BcxCCnqcvsYyQ0M03vfBVWhbn
JTg3AT1CvkJESTXnKThXgeekoailpI9FetaiZqKBpPZbObU3HcZ5DEHUDYI7
/u9B3sSX8xrUbVk5NpypxkERUznPQfRHbYLBaxrIfZtESX95U5Iway7w/bny
6qkkofoC5s1oxWT2Hvf1KxRGj7oHSg5FsMffDJ7XrKUzUzs4V0I9g3sTo1Zv
mtHpgYcNYzh/QtWdTkHpxj+QtuAp51OI7TZvfGt4B3MnGmJqqaKwXXsk51k4
10JzWw6Q7R/CIHpkEedeOP+C3vFfMf10GediaPjHWeBsegYOdJOHnSNeSQZ9
6RTqLNRgV6Me52pEWccoLAhuQOMsH87dkI33SkCmvRi4/7i5uJouPDcN0774
0KEr+gmHplyhgWucsDD8DOd56LqZYaCl+ReM5JM470MTCxIx7hPFlsFaOHy5
QAY9jeZ8kDh76hrqOvABEc6HwM0ndzlHRAKSPbCltR11nudwzoimBbjBPKsw
6GM8GNz7dhedGpuNn137wPkkoqsVRG/dTcC6Ea84v8Q5Jmgc3QAL2p9yvom0
tuui52obHEZzqX6iX0bmME/6/sQy5uWX8f4h2Bslg23PH/D2ijfnp6hcfCGu
nPMIS8/Jcr6KJB/pBVnKuYLdgFhx3okSIpXxh/gbFzmXRWaMjsZvVv+wXDuO
c1tEb3EMDNp4G7p/lQPVE8M538U5L857kV3/PtAPNxLQe2Im58GosN4bwl/8
AQ8LkfNiJKPYCT8VeqL/9Q80/GqMxMhjMl20WQPDNRQ5b0a6fRQhKOw959A4
j4bqP2vQZ3sm59Sok+woOLtbD35kbiehD/Wkrq5FpHj7KVj7YQfn3GjuUhGn
4G+MqTnDOTgiK8mF0OAUuP24hnNytOZ1LFVTihN2vGkXfC/1wZ9fonBHwjXO
14l5O+LhQvE/+Hn2BufvaEJyKL5SCMbh3d7RXTqvBcsjPcXUpo/UST+RwgBZ
6NY3E+Il+ZzrI1d9/PDQ91b0aU3m3J+Y27AJNM9vgRU5oWTUbo0Mj09xZNH7
FZBnMJZzg9Rb8gTP+NdxnpBzhbBoWjWEttzhvCHRmCSLtXN74bQgV7EIIyRP
+8thj+yLeC37GOcVic25XGjL+sM5Rs4zoodDBupNisCtAVLOO3LukfOP9Nkv
NToyfSxsUUmDEzE3OScpDGtIxu8nO1B5fijnKInJQD9IJadh/+ZY4pS/Q7Sx
2Uj8Skdz/pIov1bFcJci1Ggu4nwm7TGV9dxN32DZp2jObwrPIs2Q8x8LjuhQ
a5170vI13bCq8BT6rp3B+U/i7FMKYQ31nAvlfChG1ZVgYnEEKprbcX6U5DdH
kr/fqKixNkka8XMKxOjcgmMyHpw7pUVZz1Cm3x/Oo3IuFTbtSIClhudh6OgA
cqJEm/OrwrvXr0nkDyNiaWKC760K0NslifOuosH5e7B3z2+Y5XuB87B0/EkX
XLB8NT47toVesDmQvmvBM5rydhHnaGlE/+lgUFn5P3++fGsOcZkQiLVja3Hf
0sucwxWLJk+A4cc7SNJAJQFerhd2LJkIZ18Ecn6Xc7z4OLEan99u4Hwv53zB
WjcPDhM/WP3WkGz/GMt5YNFY/xipyvWUxMpaoMUDKU5e4c35YbKspBhqw1o5
V8z5YiwzDEfLTnt0HrqavrOKEqbPd6ND1g3lXDJdkm0JPVwqYJ1eKueWhde6
D/D+rW+4w8uTc83knqk1LNccDzx/FffVTdA+PxjUVA5yHprsNpuHWxpqsVCj
lPPS9PDGACBWr+HQznOcp5b0KuuNqSaXaPMvURh3KU1sXWGBg9pjOIfNeWyI
PF4DOuVfOKfNeW2000rDqPdHUd1Olh5YYMm5bnHpq8fUfu3NDK1CR8jXeQYd
2X6cA6du0S/RzvsbHp24nnPiZIOcD0S4zYYDz/sSv4odkv3jPpObpoTz5WRN
2UG8vbwGix7ex4lFFyZ28edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/e
xZ938edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/exZ938edd/HkXf97F
n3fx5138+f93/ryHmW5cF3/exZ938edd/HkXf97Fn3fx5138eRd/3sWfd/Hn
Xfx5F3/exZ938edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/exZ938edd
/HkXf97Fn/9/58//D3/8rSU=
"], "Real32", Appearance -> Automatic, AudioOutputDevice -> Automatic,
SampleRate -> 8000, SoundVolume -> 1]], Audio`AudioObjects`audioID$$, Audio`AudioObjects`buttonState$$ =
"Minimal"},
DynamicBox[ToBoxes[
Audio`AudioGUI[
3, Audio`AudioObjects`audioID$$, Audio`AudioObjects`buttonState$$, Audio`AudioObjects`audio$$,
"AudioData", 1., ""], StandardForm],
ImageSizeCache->{28., {17.1425, 23.}},
TrackedSymbols:>{}],
Deinitialization:>Audio`ClearRef[Audio`AudioObjects`audioID$$],
DynamicModuleValues:>{},
Initialization:>Audio`CheckID[Audio`AudioObjects`audioID$$],
UnsavedVariables:>{Audio`AudioObjects`audioID$$}],
Audio`AudioBox["AudioClass" -> "AudioData"],
Editable->False,
Selectable->False]\), 512, Automatic, #/Max[#] &[
ResourceFunction["DiscreteDolphChebyshevWindow"][512]]], Spectrogram[\!\(\*
TagBox[
DynamicModuleBox[{Audio`AudioObjects`audio$$ = HoldComplete[
Audio[CompressedData["
1:eJztm4k7ltv3xpuUiiKaSdFAURpMeZ+9Io2aNaeUNEpKNA9kqsgQRSFRhpIh
UuF99iIRKk6SoUgjColKSfTb+/tv/JzrOudcnVN4n2fvte57rfszxtp+xfYe
3bp1OyDL/rFiyyETB4ctRyx6819s27Jn+rQ9/H92Z3/PUuv2v7+KHt6H28tr
YE3ZQXB9v4reNCW4f9xn6lexQ3rgeV8a4TYbN8j5YGzMX3p04nqw8/4GbtEv
YcqYCNKR7Yf5Os9Qq9AR7dfeNF766jH5dfGecGCBJVW3kyVR74+CnVYalFuv
gJNLNVCn/AtGHq9B3SlD0NvBHAa1x0DrCgsYdylNaP4liqkml0ivst4wVGWB
9NDOc0isXuPhjQE4ffBdUqhRClsaamG32Ty4m/aNqqkcRO3zgzHuq5soL9SL
yzXH4z1Ta7Q0WUt3eHnC/Vvf4LXuAwiz6S2u00vFHi4VuCTbEqPfmZMh64bC
9Plu5J1VlOg8dDWx7LSHMsNwEN50hzwbW6wNa8VlJcW4efB5OnmFN1g8kEKs
rAVU5XpKjfWP0U0hDcL2j7Fk9VtDepj4obVuHp5avBorRk2B57cb4HFiNfzp
Lwsh9iZ49kUg7lgyEeHlejFpoJI4/HgHLZo8AWVmKAj7ll6G2rG14DIhEJZv
zaHJpAQNKisxov90LC6rJilvF8GuBc/IBZsDM58d20IWLF8N40+6wIc9FmSW
7wXcu+c3Gpy/h0aCm+DtkgTvrQrA0sQEIn8Y0XevX1Pf4YfEEyXaZOjoALrU
8Dxu2pGArko9MTLsKMj0+wNFWc9gbM/95JiMB8bo3MKIn1NQY22S5O83KuQ3
R9IXY6qporkdSSyOgKi6EvBfuAYGrzDCsIZ6dPYpxXe7W6jv2hlQVXgKytd0
A2ude5IFR3TIPKWp8CzSDI40OYvLPkWj06Zv2GNqACa5lBCN5iIIdykC5deq
MPFvPvUrHY02NhupU/4OYf/mWJpKTqPJQD/88nMeVZ4fCt9PdsCwhmQ41TNL
PBFzE7eopOHI9LH47Jcaaf7kRt5gfzrn30m6NUBK9CZFgIdDBjgr9wC5h67Y
lvUHbc7l4qbP8+i17GPQI/siPO0vB0UYIZ0W5CrUzu0FGpNkYaXlBRracgcX
TatG3+OrcEakCZzxrwNvyRNIan1B8gzG4qL3K9DjUxwdtVvDeEVOKNU8vwVz
GzbhNbmHgk9rMhz63gpXffxA0viWxkvysVvfTIQBsuikn0hSmz4SyyM9hV06
r8Xh3d6RVwrBkJAcChu89cnPszfwQvE/zNsRj+3Hfgk7Eq7Bzy9R4HupD+x4
0y6qKcWJNa9jyfnpN8jtxzU0NDgFZSW5eGRwJ42pOQNT8DfkLhVh+w81svbD
DizefgpdXYto6EM9yY/M7fTsbj10kh2F1wYkEp/tmaD+swYiBy6Hm8/mYVDY
e+z2UcSYtak0XEMRFm3WACOPyST8aozU//oH8qnQEzKKnWBdSS/qYSFi+Is/
KKz3xuHaX4j3xEz4cCMBdv37QKbf9qV+Pm5UoWQYUT0xnHT/KoeDNt5GvcUx
mNauRsu14+Cb1T+YMToaoqsG0fgbF1Eq44/zTpRQuwGxQpZyrph8pBfO0X9E
S8+x9zHnEcjFF4Lq0h/k7RVvtO35A+2NkrFi0w9xlvcyeH9iGWQO8yT6iX7G
w2gu8VxtA63tujBI5yld0P4UG0c3YLLhQvS6bA51I17BrbsJoKsVRBKPt9Jn
1z5Qp8bmDPe+3YU+xoNxnlUYpgW4YX7dRKLzPAdaWtshINkDvhU10ZtP7qJw
PgRdBz6gs6euIQcdPYRBT6Pp8OUCbRmsBXGfKCQWJILOBBliJJ+EWpp/cd3M
MHTuHEsKw89A4BonODTlChm6op+Y9sWHLDw3DW4uriaRO1RRpr0YN94rQeO5
tdQ4ywcKghtA1jEKzCYmCrsa9bDOQg0HfekUd454JT3QTR6dTc9g+MdZOH3M
Z5J+ugy847/C1hkmcKd4EUaPLMLtH8Iwt+UAfWmbQ5x6HSPbtUfS1FJFMXei
Ibw1vAO221gdm7mCpi14iqUb/6C60ylUONxMDhvGQEanBxi1ehPP4N5U97wM
mZnaQZ7XrCV7/M1QyaEIR4+6h/v6FYrJcimQN6MVEqovgPLqqXT/4QOYMGsu
9pc3pfdtEqWD1zRQ/VGbMGDVTzooYio0nKkGt2XlEHywjMib+OId//co6gah
oGMj2psOg9pv5UQz0UBapGctaCnpwzlpKJyMXww/Y3pgREk19gj5is1z9DFl
iTm8SsuCzTe9wDJCQvQ8fek9a22xvT6EJD3sLfyatB6V1bNRbtUFVL97hBiE
/Qdyiq0QONUetr34SjP9grDygDWGR8+lI7YYCdsOxdDZwzVR0XgPVWvbBD5F
VfDMJB209M8L7oPuYnxQIx4RPNFPz4D0nbkCnloMBvn6aGFyyk0B146FA5tc
4btaTzCtMkPXR5/x8bEKHLkth7b09oFA2VI4fcMTzFr/SMqimmhQN2t6qaci
aay6L2oO3oT6mxORLl6D/QYogGbRJ7BprodfqVrwX8Nc1B2ajCEe+3DHqr70
YvxEMmXceJq+sYbOf5slzcg/CpLaYqi0ugTbVf3owORidB/ThGGNlqgVWUsW
tbvD9156sP7LV4EcNRWWR8uAxZ0lEOxwiGypOYSvnn9GbQMp2lYrifLsPRbt
fg+zZJ2AyOtT4zIddJ6TS1s8kyRJtsPp+n3Lcfjfi6jRry/+frgalM81w4BZ
5bA27A4xkvHCBLXHGDFgLyp2TJdu+XCTbN3gLKl84UlPFfUid0xPw/w/CMfz
NoKfowrarPmMSZk1OOX5SIy9BOBreQ0M382DXS9TBfm7xqKeVgZxVBgC+xfK
So7neePsDW/xxtlgvLM2khxyKgat2E/Q3m0BWN1/Tf8s3IZWkt6Y4aMn9jEY
TJt89NFc4oB55Ufp6qOekGPxHWhvKTS9NTce1ZiI9UUlWPR0HR6y1yEXE3rD
5r4m5Hxoi7gv3ZrMrz0OT+9FQ9ohOZBv345GYism3C7BfomhdMYMDwjudg+y
xpvDdBPdDJ8moK+DTcjs3tkkxWkaTXcIxEGbCtFJewu+9ZkAmeu+wOnR1TCk
Vg6qZ+nhrTRv1Pykiq2H54skIUq0y1ZAS9DHGzuWSP7KhoBkbT24VwaD+b9k
mv+6CA/mVGBE7nT801ZALrobw51l8aRjYKo0wPgkWfhhG5yachZSqg6SC+/8
McbgD77ENLRc3ihZlXQLBn17BDunCqCopEoTVqTTc291JDu0VxGn6iBaNyIA
725NRS0XeayY6gRzFrTBqPJCODLJk/wbewrzX0dinOwEbFitIbE9OVh4ZpZH
n55so8P72ZA7G6Pg17ZX4BmwBVg/R4uCOkyd8hL1/f9Qz/oJ8DpvL3Tq1JCW
u4clHurryO1TpjDU1gISN6iK3Ztj8Cl+x7s7g7D+TBbJfVsAihFPYGGIKki3
pVKLYQPRzmokjYyKEWR0Uunhc2fRfFsQXlLaQ3u3X4FHOzoBDqfCoxEOotma
6zipPRl9rqmh1steJKduLokoXUm9NwbS+3FIbu2Jhoo3rDbMl4M53s7oN6YN
A6pzsWTOVjpn4V7oXnceKrR7QKW+jpT1D+FIyBAYaTkY5i72ppfz72LZ9w8o
q26FK6WGMDLqI7Qo5cPp86/Ivsih+FDXBMf/8qWBtnMkmZPv0A0GDtiwxA5l
enkL9ktSwPdYGww3C4Txjs/oQ89slOzKwN6VvTGnfwjx7sgkhxz6ifJefelA
5Qbi9uwqpFy9DvmTNpBhoZHoX/oPK80T0T87Sbj05TIsnRAOTW7dIdsxX3x4
IkSqZv6MGFxOI6/H1dFekx6ga/+n+PeXLJpMd4dEk1bwqJHCKDMjsrRpHUqy
9+KDIek0tNTH2N/Rh56Eefh0zCQc6BtD5jk/hK3NX6BdZj0oLySo8rUK1drS
Mdg6nc480QuqJimCaXKdsLC8l6hk10r0En1haYUL9O37nzjxuxRXn/iLn876
YsX8UpLyOg0MVtyE6Pxqcm7cYXq/ZRadO34jmbLEgCidU0S5o8n4NCsep3w3
o+OuxkLDyU5Qt4yBA95vxX5HfXB00ll87ptLL4sHBJ1MDTrsyBB0/FNBrVfK
wkKVPPAoeQG7H/aEuXZn0Cv+G44fcgfHWSnSCYamkKEE8HXnZqL0WV6i6vCW
hJx2AvGjAPcl2VRjWSGuXdaE6gdX4GxXE9h9pwSyFOKg9tYVcolU0Z0elLaf
XS7oXTUWTtxTRaMHN/Cgnhdmb5cjuamPYDH+hf7rz8KBK6/p+KZ49L94EQ+P
SqYP7aYStf/8M24o5lOtPEtakKINzy0ewfOMVBCWTCSjqm+jus0f9CkKw50r
ehIbFRfod3sbKF87RzLOW0qvzE0gCzXNwG7+T2JrpoL/9S9FO+0KzMtqo7Kj
zsGm/XXwIPQ6/BpfIVxcNQHHLpJHS6uroqJqnVS733C02ueHs90X462sN6RC
rhxC+zXD16T5YKVvioo983Gh/2UMbTlEh9jfJieH65Kzq9fS3JBVYuMNAO22
+/Dj9gXoP2Ya1XQoQFmzP3i33AUV+lUR1cpwsN7vDP2s3Un92BwxwnwR8fo4
EFqfHSEz1edhlUYJmrhkYNgMOapimgjN/t+h1/ML4C9VoPvebMWkdD3M6lSj
wT9HiwozZPDPNHuclySD87ymQFjBOwiQr4TEsZ+J3ORzeCWiCutvB6KCf5CY
4tYXBrankA/qh8So6E2Cn44JXLW/Ad+a1sFHtzba3a8aTdS/4cZ2CcbNnAW1
nemwKdUD/OMFUvvPjvbM65T0K0sn1estBDufzdholI9eBsFoPXotUelXCI5D
foKwwQG2zX9Fn2f7YueSlZhtO4Me/DhHcrkjn47+aIiZkz1psf1mmJ72Dhrk
EQavKxM+JSbiRpUvON7XA+NKh5IVOqagMrIXzDQ2Fhx65guNl6aBtr8XzB45
AKL+M0Fl3XocfrQSHWaU0jFeZyBp/X8w8oQbDJwGwk2VYurQOoR9TzPyIi1J
zFXfiVqe9/CS6lbMceoLCWkfwT6iAWj4FOiz3xjn5t3CTqdtGOjch8bV/RTM
7fbRh7d74J6/emK3bs7gNL8cUl+EwGHzE7R4WxHeXNCI33pb4Z6hL0hq6DEQ
2sZBofSR0P/4NSHcYghoDbOCg0vOk3KDw+j4uQGrbDKx2itA3DA0AfapvQHD
Qw5QoDiMyh5VxelZkfRP5QHhHhlPb2RuQq2cMPz7WQm7iyvg2IgWyD/2CrxP
ZpFsTXd8kJmJCue342jPAqm3tzfJumMnLrGIpAPkOwQL9o703XNhqNIueKQz
GBv21eK0KzVo3TAaEx5NB9bPwSXHGFYF3BbmWDumP79WTSocx4GtTadk4yMf
PNr2EU95hOHr2X7E3LEQYn6/h5UDFkKJ+WN6ZuVKfFnVQFcvjpfaT55GZ56c
i1XyLnhxjy/91d8T9vj/BAM/hJBVo4SXdrewhhZhrPJq7NddkUgWNJC+ss3C
4hHq9OX5PeR7gBvskUmAD5OGgkL7FnSxb8VXGqV4IjCO2rNnLfcvAVTPmoKp
4wDJeq3e9NB2D1L2qorU7dWinmbByP1533e2OCJcDcbfqIVJ49+A+TRFeDxJ
C0c6umFBlQLuHDVJdJnXIVadUMeDu+ZgU7mZ9ObGUPim2QQbNoSBrtU1Gj/p
CX6bU4qLC6ejWuE90nfYRCCnvImX8mwxSM2bvGp0hLwCP+jMOk9yy/3Q/WI7
fr0mRcnHnAy7xBuQMg7BdYshfN3QgzZMvkwlu2KFg26nyEq9EOpzPRiPa0rR
789Q1DCyhwCV3xBxrgim9b1IUjUcMHNeCHL/8TjAeaZ+WZA01aaRNhr0w9hZ
a4mJayyk+1aD7nVbOOmiiU4LPuHU7S+wKLsbvowZCcknNoLCuQKi9jHZeLe2
C0n3sYDjxtbg222OtDIoFk+nt2Lh1hAs2ZdATp3NgZEbHsO6KBU4FBJBfVP/
0OOvEkXT+W+FDX6Z9Pc5P3QNvYopwWdoxqrLoPm+E/Yl3IdhzQXSCdWheNz9
Nk4sGI4G3coF/WEyZKSWL52gcYsu2pBFFJfGwfv+ecD6B5yaeBSnDP2FmkW5
+KbyODXM3Qx9XrhD4Jwm0v+Oa0blZV3S8lATtj9WB9ne7rTZ8D7KWtbhi1M7
sdVvCpRtegv/ueTCgZpq8nNOf6xdNAWNZLbTsUdzJbcWPqILjFzYZz+GE/qO
E8xNU6DqcjsMuR8EZb/TaPEFEY133kONll44I9eTGE4PI8OPF4oriyZQtXs/
SZtBFDhtvQWzFjoT/3XXsMP2HxqWJuEuw7WCfJ8A+DU4GCqdfhK5TyGi8Vw9
oSSnmTx+WkS8RtXR7uul6BH4HBe+GIRrzVxg4MbvED9ECsduLCP23RehnLgR
FXZep7HO/kZa+2KpQclaPLLNEE99ukpadR8B8f0KNdHWMMh3Bs7/Uo7S6PvY
pE7pN+EbKU7qIE12W4TSrbPEW/U9IWZpEAySnoGsxQGita4Uf6V34J39FzDS
+SGZvzIFZl2/DmPHviIDGlZQ7fwWUXOSPzmycA3R2j0Y3ckDHNjnLn45tpv2
xihQ1O2AxcaxYFkWJuoYeqK+8mkcIdynqafGCNEV1rRwtyZ67v9GFfb2gVne
T+B7QjlkSuRhSz83lPxoQEXvRPx5eDzVbZ8O49fpwH8LdMlLcYIk9/tv0qTj
CndrF0LktDRqZVyEw1VbcOjy9ahqZgA5bYUwUTYGLlWEkrMJj+i0VZfpqKcf
hAUznIXEo+Nwf34cRmb5494BFcKKmdmgNaIDKu96wcywx7TX+2g0neeLz/EW
jSiSJ3vfXBLHRdRTI9OTtCVgCrzdmg/tThkgPltKjmy7iV+m/8YEmauoPClX
aFM+AHmuq6Dc4QDZu8vbuCLlKdkUtQr6NMqAk9MIfJlcjm5Lq/BNkwxOX+QO
feo/gL5VBDTf6RTKPg3DM/KtdKNmjfTx7LfSqr1jsdY2GGumrMeo9S9IuE45
+HZnnoYuhQnOBjj1+kMc9SYQdckROkUIJA/DC4RdO73o0lB/0XnLXDi8m0Ju
aTDUVyrQBCEPDaVt2Bnlimub88iZNcFwZMIBKM4/TPzuuoj19WdIXrcxsHKu
D+n5cz4+cCjH2dGZOMF1Kj0xNQ7s3b9B0pYLcMPtg7jMaCW+zhuLk3NaxXh7
K/FtqhK29XXGnBYFHFGkDaHXPsBeh2qwW/eHHPnuhjVrytH8kT+e2PBAvPfv
J4lN8iGp8h9FDWGZMDfYHF7XxsEc7e3gmttANT68wdxZzRivPxt7qujB6F53
IcrGBWT/GhNjSmj13RKB9XMyLyFQ2DB5O477W4hHf4ShzyU98lf1CQgJ30G+
0hEWTsmltmWeaBc0B03s1Gjt/MvS2Nx6Gp6wAP2VL1MvrS1QbfwJFl/MBvG6
AlkhH4c5M2tw2Sl3rD3zQ/CbMA2CFD6R0Z9/Gd8pfi+0wywovBYAFWbDwWgs
wfeTG/D+yGq8YV9DtZpOg+G6ApD/7gxLVA4Jq8en0gyNINHvxFHiY3xDtDi0
H81sRdxRthdz9/aAOuEDdNY0/M+fD/8zBb1NrqPivXU453MPeuTwFeF0eyg9
azkIx/05K44yPA1jllTByREREBS6jurkPMEDMvV4dv9mvDwCiewQWyjbNQR+
61wU3ANfCX38x4PyHnsQw8PJ48JD+PZSExbMe4QzXCrFVZ9joadDBTSp20Pv
kb/FNj15fLP+BF0686mQNE+Xntxri/Oso3Di51HYOWoJtAgtMGhNJTTe+Y9k
7ziJX5TT8a/5JlSzUhIjnluRjU296W5/kcoL9cLex+egKucpDDB0hB5u8tg0
/hOukK1BnyPjcEwfTdjp6Qc1MlNg5tMwYfb8ScK+/O5wrW0GhCfZCHqWftiq
/xlnLI1Eh9JjRHZsATS9qYYtOxfCvrMp9PPs2eix4SnN1b5ovOXgIqrRuAo7
vpzBOQMj6SxTD/Cy/gVu+Q8h8s0lYa30BlYsK8CjV5bjDOtG4bnXExIbLxFG
ti2i+y8cIJ2W5+CGWiqs+zYGGm0t8VzqT4wwKMP7KWl8fgV9HsSA1nQjGHjR
V7JjYKi46k0cOb20jYS/VqXuySFoXFiB2ZsPYs3aoXDV5yPsyawEhVplSJip
issUDuNE6IlHn/YQKxU0adX76bghciUeKlAV+y0JA6/AFtgRHgFFQeep47Rc
NLAqxt1q0zF+23UC14eB2n+ryL2CK+JrMYjMvusC3guDYUDYNQKHfHG7+19U
0UG0VRonfnC9Coq90sC4eBrMLnwhyvbfT80VRxHP6ovknUYY5f6jKukhGjqp
49yMnWDg3gpXyorgft9I8kFxG049GIAlQ5TwWntSxvovF8Qzqn3x0beheLP7
QuJsyu6i9UdYYu8Ex6LVUM7uHQ6f9hxJRE8MDBoIZr/NQeFFPFGc/j5D2zWQ
rNe3AdW+++Fsk6uk8VUs+i1qwz+q4Wi5JITca0LIvfMQGlpHwIN4HzptRRkV
4y9LdxcPIHkeBXSVJAgDEqNwfGAI7bEhCP41dkKMVxqArLzEyuwSsv6Buw2V
UHlknDBH5qzws8ddujszkw6LziKa/yVC/5/PYHToaFj90AEv3/iBlWtyccW8
c3S2qQW0Kx4Dr0/lRFm55oF3vQ2ZlzwTmq11QdA4QmFWGobsaMC/XvtRa+J4
0Hn4GnI9smH/rw9k0dpOWmaiinm6E6lcupqQPbCUXh5xFhe1uqGtx2TJ9RfJ
8GJRB3h+uAKCXzT1tr6PR2Tv4ISlPfDd590kbvEBcrpSmwYumk/3fOwg9xfF
QU57EkxcGkAuMD2tG9CJpr2SUX9+jGRCX29oS/eDV041xDVquzhkQoWQPaI/
DBFriOP9GpqtkYm5xaWoeUEFcyVH4azSN7CtTofBv7eR/awG+WxahPtdvajO
lovpzWZZ9LPqblTPn4P7R10kSYdzoOxJMzyp2w3foydi/cUX2NyYgkb+mdRj
bDnZ8r6cpNffzDg32lXc2NgfUuKuwkxvX3h1dIKoLp+B+706sUb+IhrUJRDD
y7eh5koY/Cf/gtx7PIXmHV4oiip3yZi1R8gsn2FoHSPi36Hp6Kh/hvYLiARj
x3Y4kxEL7fnGonz+KcQ9jnjTK5rKzUyRyA73o8GzZ+LtRz0x+LUMvAkoBCvD
KpjqPQSeNJ7ESa/qsOpKPI6wNqIN1ePg6dqR0FbVLgRVD5aMGikLX229YMmf
NXBfJYFeEIswx+0H7sncgpdqtEHjdx4cCY2Egwlh5MCb29R13k7630tdMvFi
jHDPTRvTfJLx3bRgZP1c0N+SBT96d8ANPA8PGlLojpvheD3qDC7+EUFvVZcL
/oIitZnWBy2f+1GL+1NhnFIh7PiRCWrHnciMG1FYFvwTO1+F4cCXZwTt6q0w
sc4MTvdZSv6OD5cYj/lCbFq3w6NDirDs31A0anqFfVXe4bucARi1zBneyFbD
rYyrEPdsIPGI7YcnVJ/TjF2iJD/xofST5hTmJ6/hm4rtuLo9lwyvKQM7vx+g
s2o1hKdro3M3KX5+4os7nhyi3J8viCqVdBjF0e5TRfHEpkVQd+YRRFRdhUFa
VaJKYg4uz/2Ne9Tc8aNJKumd5AftxTaQ08OGvB7aW3TsFUfmjZ0G9S7XyOX+
C3G7ZSVGnslB2cer6YDqaFBSbARbP3+4P/CmqBBohgOclPBRcKw41uWs2O3m
GFTecAZ37VTBz/u14Gy/T/Dm2HtwcZaBF9qnUOlBMZ485IPyi0rE6mMVZOCy
FWTEYE3aMdRAOLlkFZwYnQJ5axxAa1w1q1dVqPSzGfOb5uPKDi2YV3gbthw4
BFoeBuTRTkWqBDNI1KQ/RMHwkZDUzxZnbStB6nEdj5BBZEDlYygsb4anCQfh
QEgy7Yg4hWar9DE7pQ9deXuWeMqqN0barcclNI7KsJ6fv6oOMl48hm+r9cii
KdGo/fMdjpN3w8kzRSFlujpYmGcR4zO9xbJhv4RrixZDzzMh4HthLIx+Y4Ry
WQ1YsvEdnu/ZSt33HQU52UfwfsBR2H7kgjChNJhKXsZosn8T9muR/Xdk/x/Z
7+O/n7A/B+zP86/Dvx6yr4vs6yP7PiL7fgL7vpR9f/5ziOznAfZzAfv5+M9J
2c+L7OdG9vPzz0HY5wH2uYB9PoF9TsI+L7DPzT8/Yc8B2fNA9lz486HsOQF7
XsCeG7DnJ7LnyJ8nZc+VsOdL2XNG9rz5c+fPH9h7+N/+g70Xwt4PsveE7H0h
e28ie3/8PVL2Pil7rwJ7v8DeM3/f/L0je//IzgE/D/xcADsfwM4JsPMisHMj
sPMD7Bzx8ySwc4XsfCE7Z/y8EXbugJ0/YOeQn0fKziWy80nZORXYeaXs3CI7
v/wcU3aegZ1rYOebn3OBnXdk5x7Z+Ud2DwR2H/i9kLL7Qdk9Iey+ALs3/P7w
e4TsPiG7V/x+UXbPgN03YPcO2P2TsHsoZfeR30t+Pym7p8juK7+3/P4Cu8fA
7jO/1/x+I7vnyO47Zfdeyu4/ZXUAWT3gdUFk9QFYnQBWL3jdoKx+IKsjyOoJ
ryuE1RdgdYaweiOyukNY/QFWh3g9IqwuIatPyOoUr1ciq1vA6hewOgasnoms
rvH6xuscYfWOsrqHrP7xOsjrIbC6CKw+8jpJWL1EVjeR1U9kdVTK6qnI6iqy
+srrLGH1Fljd5fWX12Fk9RhZXeb1mddpYPUaWN0mrH5LWR0nrJ4Dq+u8vgus
ziOr98jqPq//hPUBYP0AWF8A1h8o6xO8XwisbxDWPyjrI8j6Ce8rlPUXYH0G
WL/hfUdg/QdZH0LWj5D1JYH1J2PWp3i/oqxvEda/gPUx3s94X0PW35D1Od7v
KOt7wPofsD5IWD+cyfoiYf0RWJ/k/ZKyvomsf/I+yvspsL4KrL8C67OE9VvK
+i6y/iuyPiywfkxZX2Ye35v3aSnr18D6NrD+zfs4Zf0cWV9H1t95n+f9nvd9
yvo/ZToAmB4Apgu4PiBMJyDTC8h0A9cPUqYjgOkJYLqCMH0hMp1BmN4ApjsI
0x+U6RBkeoTrEq5PgOkUYHqF6xbC9AsyHYNMz1CmawyZvqFM5yDTO1z3EKZ/
gOkgroe4LkKmj5DpJGR6iesmwvQTYTpKZHpKZLoKuD9nOovrLSnTXcj0FzId
xvUYYboMmD4DptMI02tct0mYfiNMxxGm55DpOmT6jus8yvQeMN0HTP9xHShl
ehCZLkSmDynTicZML1KmG7l+5DoSmJ4Epiu5vuQ6E5neRKY7uf6kTIcC06PA
dKnA9Kkx06nA9Cow3cr1K2U6Fpme5bqW61tgOpfVqzBgupfrX66DKdPDhOli
geljZDoZmV7mullg+hmYjgamp7mupkxfI9PZyPQ2ZbpbYPqbMh3O9ThluhyY
Pgem07leJ0y3I9PvyHQ81/MC0/XA9D0wnU+Y3heY7gem/7kP4H6A3cFKZP6A
+wTuF4D5BmD+AZiP4H6CMl9Bmb8QmM+QMr+BzHcg358zH0KYHwHmS7g/4T4F
mV9B5luQ+RfKfAz3MyLzNZT5G5H5HGB+B5jv4f5HZD4ImR9C5ou4PyLMJwHz
S8B8E2H+KYP5KML8FPdVhPkrZD4Lmd/ivosy/wXMhwHzY9yXicyfIfNpyPya
yHybyPwbMh/H/Rz3dcD8HTCfx/0e933I/B8yH4g8f8V8IfeHhPlEyvyiwHwj
MP8IzEdyP0mZr0TmL7nP5H4TmO8E5j+B+VDC/KjIfClh/pT7VIH5VWS+FZl/
5T5WYH4WmK8F5m+5z6XM7yLzvcj8r8h8sMj8MDJfzP0xZT4ZmF8G5pu5fybM
RyPz08h8NffXAvPZwPw2Yb5bZP6bMB8OzI9zX879OTKfjsyvc9/O/TswHw/M
zwPz9QLz99znc79PmO8Xmf9Hw3UFqNV0ms8FyP2R1fB+cgOfF/C5ARZeC8B2
mIV3it+Loz//yghS+ET9Jkzj8wZx2Sl3yJlZAyvk4/g8gi6+mI3Vxp/Qi/V8
f+XLJDxhAcTm1pPa+ZclJnZqxC5oDtiWefI5B5GvdEQh4Tv+VX3C5yD06I8w
GPe3EDZM3g7zEgJFvv+ovlsiGlNCZP8a0ygbFxzd6y6fr/A5C+TOagaND2/4
/IXM0d6Or2vjcG6wOWoIy8RU+Y9CbJIPvffvJz2x4YFg/sgfataUw5Hvbny+
Q/c6VGPotQ987sPnP9DW1xnepipBvL2VMDmnVXidNxaWGa3kcyMhacsFtHf/
hiemxvG5EpkdnQkPHMqh58/5fO5E87qNwfr6M9TvrotQnH+YHplwAM+sCebz
KtoZ5QqG0jZIEPL4PIvklgbj4d0UnbfMxaWh/nzuxedf4hQhkOqSI2TUm0CY
ev0hn5PxeRn6dv+O4TrlfI5Ga6ash1rbYKjaOxYez34r2ahZIzkj30rKPg3j
czhR3yoC+9R/4PM5PqcDt6VV8DK5nM/v+BwPN0WtwoqUp3TvLu+McocDNM91
FbYpH+DzPzFB5ip8mf4bjmy7yeeDtN0pA99uzceWgCloZHqSjIuo5/NEIaJI
nj7HW8R0ni/0eh/N546k8q4Xao3owBUzs/lcUozM8of9+XGQeHQcLJjhLI56
+kGctuoyn2eSSxWhdKJsDOa0FfJ5J597wnDVFrAyLuLzUHK3lt1tHVfM/f6b
vhQnSP9boEvHr9NB3fbpfJ5KFL0TQfKjgc9Z+bwVvyeU4yzvJ6iwtw+fx5LC
3ZoQXWFNUk+NEUcI94m+8mnQMfTkc1xhsXEsKup2/M+ffzm2mwzscxfcyQPQ
2j0YjixcQzUn+fO5sDCgYQUZO/YVnXX9Os5fmcLnx/TO/gvwK70DrHWlfL4s
DJKewZilQXirvieWbp0lNNltEYuTOvhcmjapUyKNvg/zv5TzuTWfXyPx/Yqt
uo/4XJse2WYIBiVrQWtfLIl19k9T2HmdyIkbwb77Ij4Xp/FDpDhw43c+L+dz
c/AIfA7d10vBa1Qdn6vTkpxmajxXT5T7FCJUOv2kvwYHo3yfAD6PFw1Lk6DD
9h/4r7vG5/XUaestbDOIQrV7P+nKogl8ri8YTg+jM3I9qUZLLzDeeQ+KL4h8
D0CG3A/CqsvtaG6awvcE4suYY7DAyAVuLXxExh7NlRrJbCe1i6bAzzn9+Z6B
/ueSi2Wb3vL9A99DgKxlHTQb3uf7CbL9sTq2PNTEysu6tP8dV+PAOU20zwt3
NMzdzPcbRLMoF6YM/cX3Hnz/ge/756Hi0jhctCGL70f4noToD5OhBt3KxYkF
w+G4+22YUB3K9yqSfQn3UfN9J2asusz3LsQ19Cr8PucHG/wyien8t+LxV4mC
b+ofcigkgqyLUsGRGx7jqbM5fJ9DC7eGwOn0VqgMiuX7HslxY2tM97HA3dou
VO1jcobCuQKafGIj3xPxfRFM3f4CnBZ84nskvk/CdN9qNHGN5Xsmvm+CVJtG
ol8WJHkc4JweuUMVMueFQKqGA99T0YhzRRig8pvvr/geC45rSsHnejCs1Ash
B91O8X2X2DD5Mvm6oQdx3WKIKeMQ7RJv8P2Y8ddrUnC/2A655f/bn9G8Aj98
1eiIQWre1Et5tkBOedO+wybyvRtdXDgdvs0phfhJT/hejmzYEIbfNJvw5sZQ
vreTHNw1B6pOqIPLvA5h56hJQkGVAox0dOP7Pr73w0nj3+D4G7V8H8j3gpBM
SsDTLBjq9mrxvSHfH9L1Wr2JqeMAqepZU5T7l4D23Zz5vpG80igFF/tWvofk
+0jcI5OA3wPc8OX5PXTxCHW+txQlCxpov+6KNFZ5NdTQInhpd4vvOUUDP8Q9
/j/xV39PvgclVfIuMPPkXLCfPI2sXhwveVnVQM6sXMn3p2TlgIUY8/s9mjsW
8v0qPeURBkfbPsLGRz58/yqtcByHz69V0znWjjNXBdwWXXKM/5e/Sng0ne9v
YdqVGmjYV8v3uny/i/ruuWiR6oED5Dv4/pfvgQVvb2862rNAonB+OzzIzIRs
TXe+N6b5x17hsREtfJ/M98qgxfT0jcxNcI+MJ38qD4jTsyKJ7FFVvo8mhocc
cJ/aG9wwNIHvq4UqG6bVPzdAucFhvs+mWsOsMNxiCPY/fk0slD4ShbZxmBp6
jO/B6bfeVnBzQSMUbyvie3KS+iIEneaXYzf2rPf81RMe3u4B5nb7SFzdTzHQ
uQ/pdNoGc/Nu8f0738OjfUQDJqR95Pt5vqcHLc97kKu+E16kJQkHP5rxfT65
qVJMBk4DceQJN0xa/x+O8TrD9/9k+NFK5ifreS6A5wNQ298LGy9NQ4ee+eJM
Y2NRZWQvXKFjynMFdLyvB2xU+QKfEhN57kBskEecnvYOi+0381wCGf3REC53
5JODH+dIs21nkM4lK+F5ti/PMxBhgwM6DvmJKv0Ked6BehkEQ6NRPtj5bIbq
9RZiv7J0no+Q1v6zI/7xAt3E3lFtZzrPUfA8BZiof4PuftU8Z0G+Na3Dq/Y3
0E/HBKOiN4kf1A8JA9tTaIpbX57TEOpvB8KViCqQm3yO5zhogHwlhhW84/kO
nvOAP9PsQWGGDAT/HC1kdaqRpHQ92PdmK8+HkF7PL2Cz/3dUMU3k+RFi4pIB
VRolMFN9Hs+XUK+PAzHCfBGtH5sj9LN2p9b7nVG1MpznUujdcheQNfsDmg4F
PLdCfty+gNpt97HxBmBuyCrh7Oq1POfC8y40tOUQWeh/GRR75vM8DM/FYGi/
ZqyQK+d5GTrbfTFY7fMD7X7DQVG1TmJpdVUYu0geLq6awPM24oPQ67hpfx3K
jjrH8zjETrsC/utfCrZmKjyvQxdqmuGVuQk047ylRPnaOdrv9ja0UXHhOR8+
bwd1mz8wqvo2zwHR5xmp+NziERakaKNWniW5oZjPc0PGD+2m0sOjkon/xYsw
vime54tI//VncTH+xdzURzx/RA/qeYHRgxtw4p4q6F01FtvPLhd3elCeWyK1
t67QLIU43H2nhOeaeL4J1i5rAo1lhTz3RMSPAoacdkJVh7dU6bO89OvOzTRD
CXCCoSnPTZHxQ+6AV/w3nqfiuSr0KHmBC1Xy0HqlLM9dEb4/18nUIJfFA+Jz
31wyOuks9Dvqw/NagrplDDac7MRxV2N5nos8zYoHuaPJoHROEaYsMeC5L57/
4jkwEp1fTQ1W3MSU12k8J0Y/nfWF1Sf+wsTvUp4jE5ZWuKBeoi8q2bXSheW9
BNPkOrFqkiLOPNGL59CIWls6qHyt4vk0nlPDrc1fcJ7zQ55fo0/HTIKTMA/8
HX1IaKlPxoMh6USSvReWNq3j+TfqUSPFRJNWnovj+Thw7f8Uek16AK/H1fH8
HFUzf0YfngiRZDvmC01u3XHphHC89OUyz92JleaJ4F/6D4aFRvJcHk25eh3d
nl3FgcoNVN6rL8/vCd4dmTSnfwjtXdkbJLsy4KFnNs/7keFmgeh7rA3tl6Tw
PKDYsMQONhg4QObkOyTQdo50/C9f8lDXBPZFDuV5QtqilI8joz7ynCHPG0LZ
9w9wOf8uzyGSkZaD8UjIkP/l2yv1dSQV2j2we915nLNwL88xkoDqXPAb08bz
jTzniBVvsvDWnmi8H4c8B8nzkDwXSbVe9qI+19RgUnsymK25zvOTAhxOxUc7
OrF3+xWeryTm24Lg8LmzIKOTSiKjYkQ7q5HEYthAnsskC0NUUTHiCea+LeC5
TXp3ZxA8xe/QvTmG5zqFobYWePuUKXqor6Mtdw9LO3Vq6Ou8vehZP4HnQknq
lJdgUVDH86I8N4q/tr3COxujcHg/G54rJc/M8ojtycFiw2oNaZzsBMh/HQn/
xp7ieVQ6qrwQ5yxo4zlVnleFu1tToW5EADhVB5Ed2qt4rlWasCKdKCqpkp1T
BRz07RGuSrrFc7DSl5gGMQZ/4MI7f56TpaemnMWFH7ZhgPFJ2jEwVXJnWTy9
6G7M87U0Inc6HMypYN+7iOdviXtlMErW1uNf2RCez5Vagj7YZSsASYgSWg/P
FzQ/qcKtNG+e6+X5Xjw9uhoz133huV+e/4VBmwoh3SEQUpym8XwwzwlTnyYg
0010jbPGm2Nwt3s4Y4YHzxWThNslYCS28rwxzx3j03vROL/2OO5Lt6bnQ1uE
zX1N6MWE3jyvTIueroP6ohIY1ZjI88wZtLcUcyy+4+qjnjzvTMwlDtDkow99
DAaTDB89wUrSG/4s3MZz0qS92wLUiv2Eh5yKeY6a8vzV7A1v4XieN89ZSx0V
hqCeVgaVv2ss7HqZKhq+m4e+ltd4PpvntCEpswZs1nzm+W2e48b5fxDvmJ7G
U0W9aOULT5735rlvqtgxXRIxYC8kqD0GIxkvng+nA2aVo/K5Zp4b5/lxGP73
IqzftxySbIeTFs8kqfOcXGJcpsNz52SWrBMW7X6P8nIpPJcuaBtI4dXzz7Cl
5hDPrVOLO0twebQMkqOm4vovX0Xuzxe1u/O8Ow1rtAT3MU0wMLmY5+FJpdUl
lNQWY0b+UZz/NkuSvrGG5+fJxfiJdMeqviTEYx/oDk3mOXuet0eb5nrULPrE
c/g8jw/6mxNBc/AmaKy6L1zqqchz+6QsqomYtf6Rnr7hiYGypdjS24fn/Mnj
YxXg+ugzz/9zDgAPbHJFXDsWJ6fcFOXro8WnFoOx78wVnB+gRwRPiA9qBPdB
dzlfID4zSUe+/1Br28T5AzJ7uCZsOxRDRmwxEsOj55LKA9aQ6RfEuQUSONUe
5RRb0SDsP841ULlVF0BZPRt+TVoPSQ97c/6BcxCCnqcvsYyQ0M03vfBVWhbn
JTg3AT1CvkJESTXnKThXgeekoailpI9FetaiZqKBpPZbObU3HcZ5DEHUDYI7
/u9B3sSX8xrUbVk5NpypxkERUznPQfRHbYLBaxrIfZtESX95U5Iway7w/bny
6qkkofoC5s1oxWT2Hvf1KxRGj7oHSg5FsMffDJ7XrKUzUzs4V0I9g3sTo1Zv
mtHpgYcNYzh/QtWdTkHpxj+QtuAp51OI7TZvfGt4B3MnGmJqqaKwXXsk51k4
10JzWw6Q7R/CIHpkEedeOP+C3vFfMf10GediaPjHWeBsegYOdJOHnSNeSQZ9
6RTqLNRgV6Me52pEWccoLAhuQOMsH87dkI33SkCmvRi4/7i5uJouPDcN0774
0KEr+gmHplyhgWucsDD8DOd56LqZYaCl+ReM5JM470MTCxIx7hPFlsFaOHy5
QAY9jeZ8kDh76hrqOvABEc6HwM0ndzlHRAKSPbCltR11nudwzoimBbjBPKsw
6GM8GNz7dhedGpuNn137wPkkoqsVRG/dTcC6Ea84v8Q5Jmgc3QAL2p9yvom0
tuui52obHEZzqX6iX0bmME/6/sQy5uWX8f4h2Bslg23PH/D2ijfnp6hcfCGu
nPMIS8/Jcr6KJB/pBVnKuYLdgFhx3okSIpXxh/gbFzmXRWaMjsZvVv+wXDuO
c1tEb3EMDNp4G7p/lQPVE8M538U5L857kV3/PtAPNxLQe2Im58GosN4bwl/8
AQ8LkfNiJKPYCT8VeqL/9Q80/GqMxMhjMl20WQPDNRQ5b0a6fRQhKOw959A4
j4bqP2vQZ3sm59Sok+woOLtbD35kbiehD/Wkrq5FpHj7KVj7YQfn3GjuUhGn
4G+MqTnDOTgiK8mF0OAUuP24hnNytOZ1LFVTihN2vGkXfC/1wZ9fonBHwjXO
14l5O+LhQvE/+Hn2BufvaEJyKL5SCMbh3d7RXTqvBcsjPcXUpo/UST+RwgBZ
6NY3E+Il+ZzrI1d9/PDQ91b0aU3m3J+Y27AJNM9vgRU5oWTUbo0Mj09xZNH7
FZBnMJZzg9Rb8gTP+NdxnpBzhbBoWjWEttzhvCHRmCSLtXN74bQgV7EIIyRP
+8thj+yLeC37GOcVic25XGjL+sM5Rs4zoodDBupNisCtAVLOO3LukfOP9Nkv
NToyfSxsUUmDEzE3OScpDGtIxu8nO1B5fijnKInJQD9IJadh/+ZY4pS/Q7Sx
2Uj8Skdz/pIov1bFcJci1Ggu4nwm7TGV9dxN32DZp2jObwrPIs2Q8x8LjuhQ
a5170vI13bCq8BT6rp3B+U/i7FMKYQ31nAvlfChG1ZVgYnEEKprbcX6U5DdH
kr/fqKixNkka8XMKxOjcgmMyHpw7pUVZz1Cm3x/Oo3IuFTbtSIClhudh6OgA
cqJEm/OrwrvXr0nkDyNiaWKC760K0NslifOuosH5e7B3z2+Y5XuB87B0/EkX
XLB8NT47toVesDmQvmvBM5rydhHnaGlE/+lgUFn5P3++fGsOcZkQiLVja3Hf
0sucwxWLJk+A4cc7SNJAJQFerhd2LJkIZ18Ecn6Xc7z4OLEan99u4Hwv53zB
WjcPDhM/WP3WkGz/GMt5YNFY/xipyvWUxMpaoMUDKU5e4c35YbKspBhqw1o5
V8z5YiwzDEfLTnt0HrqavrOKEqbPd6ND1g3lXDJdkm0JPVwqYJ1eKueWhde6
D/D+rW+4w8uTc83knqk1LNccDzx/FffVTdA+PxjUVA5yHprsNpuHWxpqsVCj
lPPS9PDGACBWr+HQznOcp5b0KuuNqSaXaPMvURh3KU1sXWGBg9pjOIfNeWyI
PF4DOuVfOKfNeW2000rDqPdHUd1Olh5YYMm5bnHpq8fUfu3NDK1CR8jXeQYd
2X6cA6du0S/RzvsbHp24nnPiZIOcD0S4zYYDz/sSv4odkv3jPpObpoTz5WRN
2UG8vbwGix7ex4lFFyZ28edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/e
xZ938edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/exZ938edd/HkXf97F
n3fx5138+f93/ryHmW5cF3/exZ938edd/HkXf97Fn3fx5138eRd/3sWfd/Hn
Xfx5F3/exZ938edd/HkXf97Fn3fx5138eRd/3sWfd/HnXfx5F3/exZ938edd
/HkXf97Fn/9/58//D3/8rSU=
"], "Real32", Appearance -> Automatic, AudioOutputDevice -> Automatic,
SampleRate -> 8000, SoundVolume -> 1]], Audio`AudioObjects`audioID$$, Audio`AudioObjects`buttonState$$ =
"Minimal"},
DynamicBox[ToBoxes[
Audio`AudioGUI[
3, Audio`AudioObjects`audioID$$, Audio`AudioObjects`buttonState$$, Audio`AudioObjects`audio$$,
"AudioData", 1., ""], StandardForm],
ImageSizeCache->{28., {17.1425, 23.}},
TrackedSymbols:>{}],
Deinitialization:>Audio`ClearRef[Audio`AudioObjects`audioID$$],
DynamicModuleValues:>{},
Initialization:>Audio`CheckID[Audio`AudioObjects`audioID$$],
UnsavedVariables:>{Audio`AudioObjects`audioID$$}],
Audio`AudioBox["AudioClass" -> "AudioData"],
Editable->False,
Selectable->False]\), 512, Automatic, None]}](https://www.wolframcloud.com/obj/resourcesystem/images/f99/f99f1472-2007-410f-b10d-5920f50a7c69/22b92ecc56f8ce17.png) |
| Out[7]= |  |
The Dolph-Chebyshev window side lobes are equiripple:
| In[8]:= | ![Plot[Evaluate[
20 Log10[
Abs@ListFourierSequenceTransform[
ResourceFunction["DiscreteDolphChebyshevWindow"][
17], \[Omega]]]], {\[Omega], 0, \[Pi]}, GridLines -> {None, {-60}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f99/f99f1472-2007-410f-b10d-5920f50a7c69/215ee4de89b9e57c.png) |
| Out[8]= | 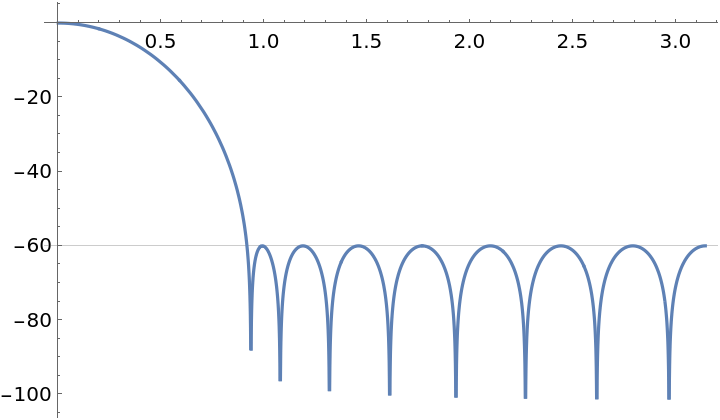 |
The Dolph-Chebyshev window side lobe attenuation is equal to -20α dB:
| In[9]:= | ![Labeled[Plot[
Evaluate[
20 Log10[
Abs@ListFourierSequenceTransform[
ResourceFunction["DiscreteDolphChebyshevWindow"][
17, #], \[Omega]]]], {\[Omega], 0, \[Pi]}, GridLines -> {None, {-20 #}}, PlotRange -> {5, -80}], StringJoin["\[Alpha] = ", ToString[#]]] & /@ {1, 2, 3}](https://www.wolframcloud.com/obj/resourcesystem/images/f99/f99f1472-2007-410f-b10d-5920f50a7c69/0611cc472fd8331d.png) |
| Out[9]= | 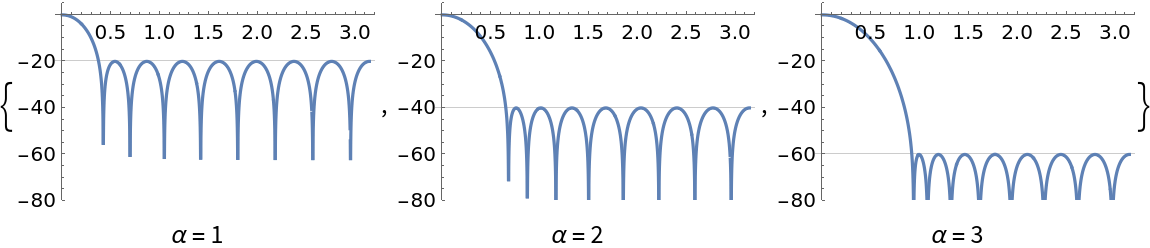 |
For small α, the window end-points may be larger than other sample values. The magnitude of the end-point impulses is on the order of the size of the spectral side lobes:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= | 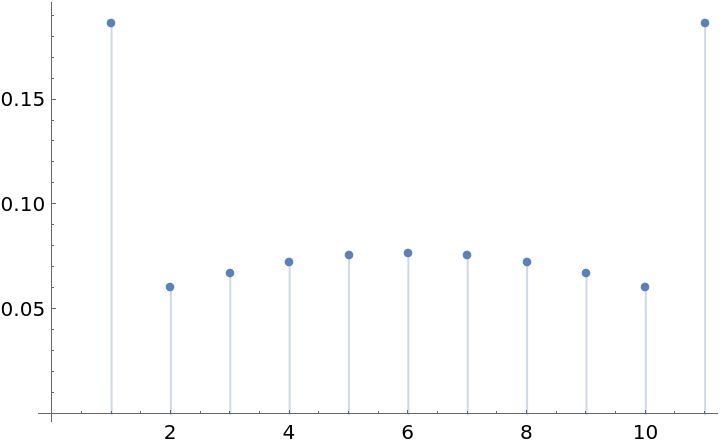 |
This work is licensed under a Creative Commons Attribution 4.0 International License