Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 WeightedDistanceGraph

Source Notebook

Given vertices, get a complete graph with edge weights equal to edge lengths

Contributed by: Ed Pegg Jr

ResourceFunction["WeightedDistanceGraph"][vert]

given the list of vertices vert, returns a graph where edges are vertex pairs weighted by their Euclidean distance.

Examples

Basic Examples (2) 

The output based on the Kreisel–Kurz integral heptagon looks like a random complete graph:

In[1]:=
pts = (# {1/2227, Sqrt[2002]/2227} & /@ {{0, 0}, {49595290, 0}, {26127018, 932064}, {32142553, 411864}, {17615968, 238464}, {7344908, 411864}, {19079044, -54168}}); g = ResourceFunction["WeightedDistanceGraph"][pts]
Out[2]=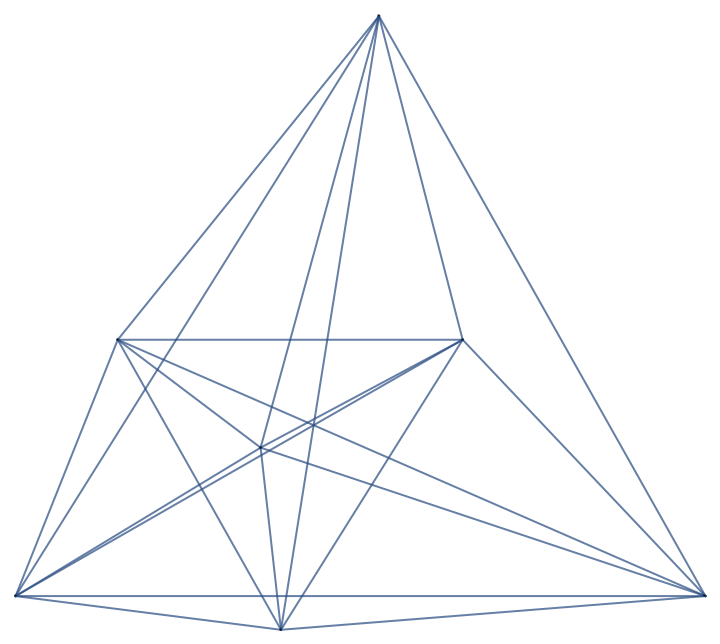

The graph has edge weights:

In[3]:=
WeightedAdjacencyMatrix[g] // MatrixForm
Out[3]=

Scope (3) 

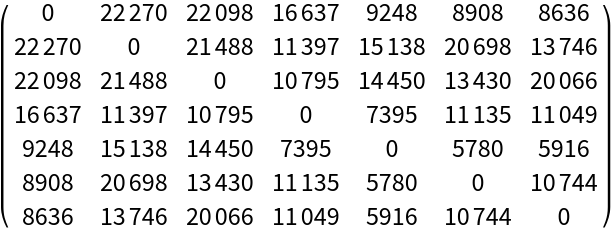The Wolfram Language has several graph functions that work on point sets that do not return weighted graphs. Operations on graphs without proper weighting can return unexpected results:

In[4]:=
v = RandomReal[1, {15, 2}]; g = {ResourceFunction["WeightedDistanceGraph"][v], NearestNeighborGraph[v, 3]}; Grid[{g, FindSpanningTree[#, Method -> "Kruskal"] & /@ g}]
Out[4]=

With weights given to edges, a method like Kruskal’s algorithm can work as expected:

In[5]:=
v = RandomReal[1, {20, 2}]; FindSpanningTree[ResourceFunction["WeightedDistanceGraph"][v], Method -> "Kruskal"]
Out[6]=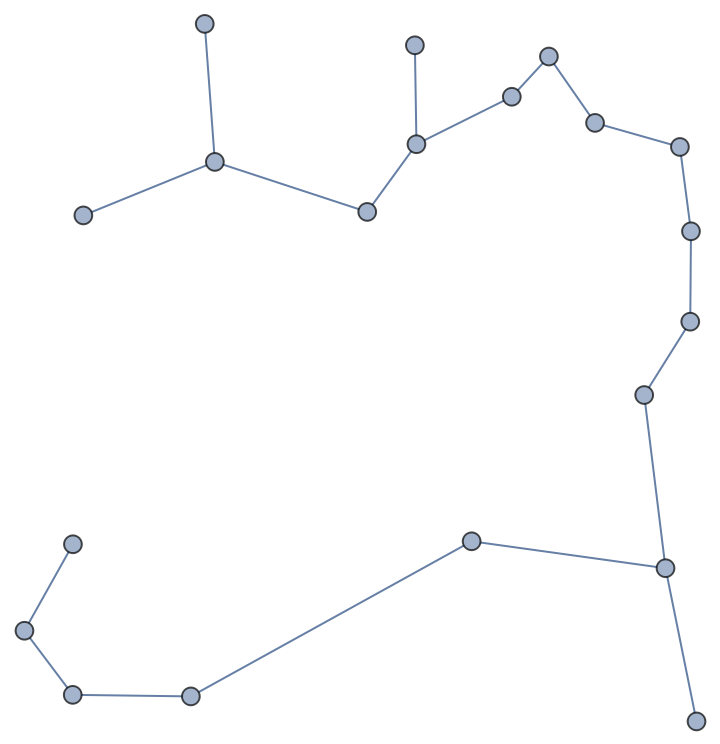

With weights given to edges, a method like Prim’s algorithm can work as expected:

In[7]:=
v = RandomReal[1, {20, 2}]; FindSpanningTree[ ResourceFunction["WeightedDistanceGraph"][v], Method -> "Prim"]
Out[7]=

Possible Issues (2) 

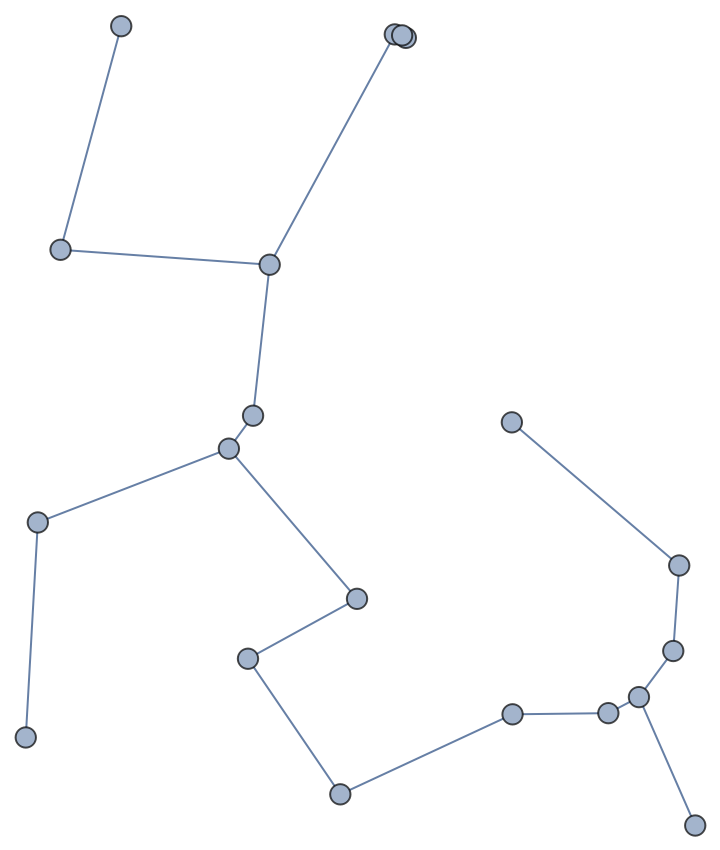Using weighted graphs for finding a minimal spanning tree does not scale up well for larger graphs:

In[8]:=
FindSpanningTree[ ResourceFunction["WeightedDistanceGraph"][Tuples[Range[7], {2}]], Method -> "Kruskal"] // Timing
Out[8]=

In these cases it is better to go right to the algorithm, which is several thousand times faster:

In[9]:=
KruskalAlgorithm[pts_, type_] := Module[{n = Length[pts], vpairs, jj = 0, hh, pair, dist, c1, c2, c1c2, span}, Do[hh[k] = {k}, {k, n}]; vpairs = SortBy[Flatten[ Table[{Norm[pts[[k]] - pts[[l]]], {k, l}}, {k, 1, n - 1}, {l, k + 1, n}], 1], N[#[[1]]] &]; span = First[Last[Reap[While[jj < Length[vpairs], jj++; {dist, pair} = vpairs[[jj]]; {c1, c2} = {hh[pair[[1]]], hh[pair[[2]]]}; If[c1 =!= c2, Sow[Apply[UndirectedEdge, vpairs[[jj, 2]]]]; c1c2 = Union[c1, c2]; Do[hh[c1c2[[k]]] = c1c2, {k, Length[c1c2]}]; If[Length[hh[pair[[1]]]] == n, Break[]];];]]]]; Which[type === "EdgeList", span, type === "Graph", Graph[span, VertexCoordinates -> Thread[Range[Length[pts]] -> pts]]]];
In[10]:=
KruskalAlgorithm[Tuples[Range[7], {2}], "Graph"] // Timing
Out[10]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 15 February 2019

Source Metadata

  • Citation:
    • Kreisel, T., Kurz, S., "There are integral heptagons, no three points on a line, no four on a circle." arXiv preprint, 2008. https://arxiv.org/abs/0804.1303

License Information