Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Cut a ClusteringTree graph at a given height and return the resulting clusters
ResourceFunction["ClusteringTreeClustersByHeight"][tree, h] gives the clusters in the ClusteringTree tree when cut at height h. |
Using given data, find the ClusteringTree:
| In[1]:= | ![data = {4.15, 4.74, 5.02, 6.36, 6.72, 11.49, 10.4, 8.98, 11.81, 13.49,
12.04, 9.19, 21.45, 28.43, 23.16, 23.79, 24.56, 21.89};
tree = ClusteringTree[data]](https://www.wolframcloud.com/obj/resourcesystem/images/f5f/f5f6caa5-8978-4a34-967a-bafa65403122/73515796c813d39a.png) |
| Out[2]= | 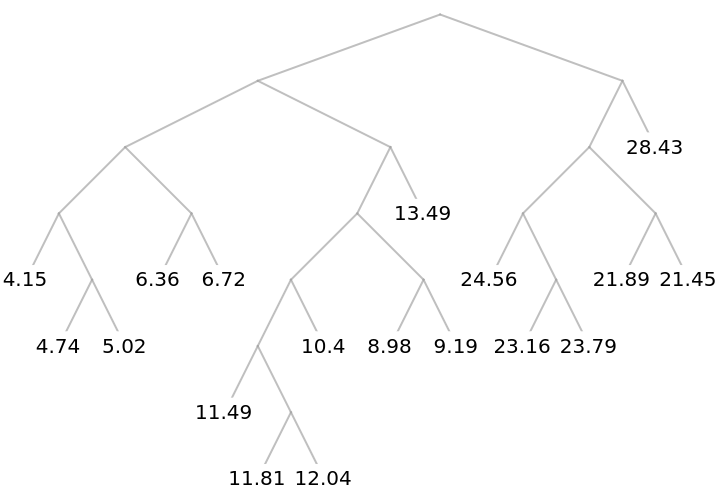 |
Obtain a cluster hierarchy from the given tree:
| In[3]:= |
| Out[3]= |
Make a list of data:
| In[4]:= | ![cities = {Entity["City", {"Sydney", "NewSouthWales", "Australia"}], Entity["City", {"Melbourne", "Victoria", "Australia"}], Entity["City", {"Brisbane", "Queensland", "Australia"}], Entity["City", {"Perth", "WesternAustralia", "Australia"}], Entity["City", {"Adelaide", "SouthAustralia", "Australia"}], Entity["City", {"GoldCoast", "Queensland", "Australia"}], Entity["City", {"Newcastle", "NewSouthWales", "Australia"}], Entity["City", {"Canberra", "AustralianCapitalTerritory", "Australia"}], Entity["City", {"SunshineCoast", "Queensland", "Australia"}], Entity["City", {"Wollongong", "NewSouthWales", "Australia"}], Entity["City", {"Blacktown", "NewSouthWales", "Australia"}], Entity["City", {"Hobart", "Tasmania", "Australia"}], Entity["City", {"CityOfStirling", "WesternAustralia", "Australia"}], Entity["City", {"Geelong", "Victoria", "Australia"}], Entity["City", {"Townsville", "Queensland", "Australia"}], Entity["City", {"Gosford", "NewSouthWales", "Australia"}], Entity["City", {"Ipswich", "Queensland", "Australia"}], Entity["City", {"Cairns", "Queensland", "Australia"}], Entity["City", {"Toowoomba", "Queensland", "Australia"}], Entity["City", {"Darwin", "NorthernTerritory", "Australia"}], Entity["City", {"Launceston", "Tasmania", "Australia"}]};](https://www.wolframcloud.com/obj/resourcesystem/images/f5f/f5f6caa5-8978-4a34-967a-bafa65403122/5cf7f5311a2c4f9a.png) |
Compute the clustering tree:
| In[5]:= |
| Out[5]= | 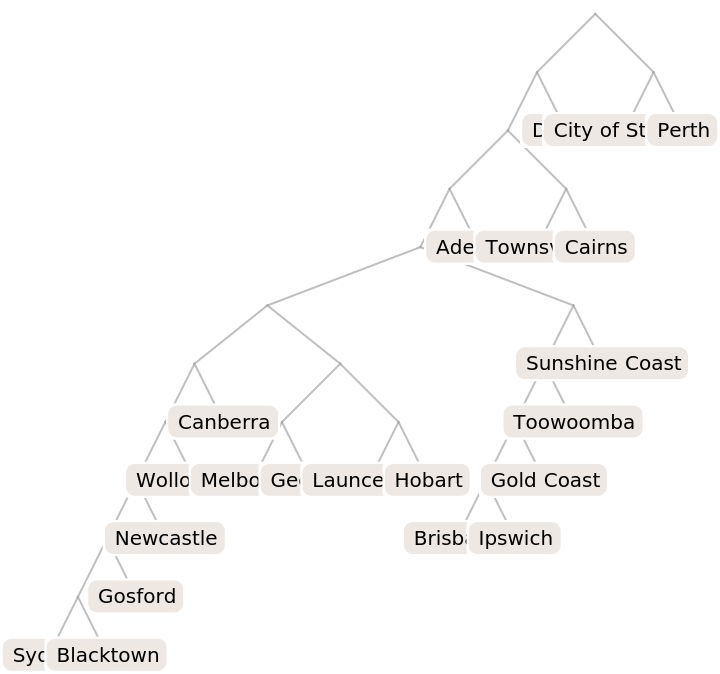 |
Plot the dendrogram to help choose a height at which to cut the tree:
| In[6]:= |
| Out[6]= |  |
Compute the clusters at a height of 200:
| In[7]:= |
| Out[7]= |  |
Plot the locations of the cites colored by cluster:
| In[8]:= | ![Graphics[{LightGray, CountryData["Australia", "Polygon"], MapThread[{cluster, color} |-> ({PointSize[Large], color, Tooltip[Point[Reverse[CityData[#, "Coordinates"]]], CityData[#, "Name"]]} & /@ cluster), {clusters, ColorData[97] /@ Range@Length@clusters}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5f/f5f6caa5-8978-4a34-967a-bafa65403122/6e010974cf2cb72d.png) |
| Out[8]= | 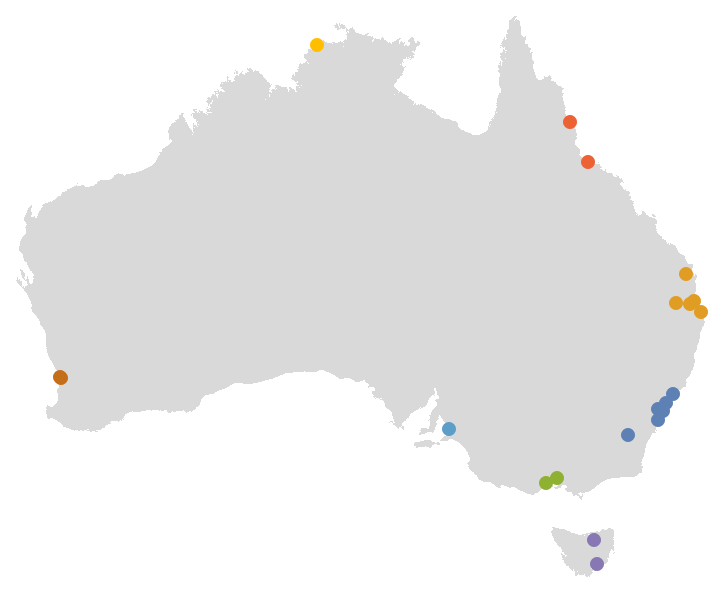 |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License