Details
Whenever the entanglement monotone mono is not specified, "Concurrence" is assumed by default.
Whenever the bipartition bipart is not specified, the first and second subsystems (as specified by the bipartition {{1},{2}}) are assumed by default.
In ResourceFunction["QuantumEntanglementMonotone"][QuantumDiscreteState[…],…], the specified QuantumDiscreteState should contain at least two subsystems (qudits).
The bipartition bipart should be a nested list of the general form {{i1,i2,…},{j1,j2,…}}, with positive integers i1, i2,…, j1, j2,… specifying subsystems of the given QuantumDiscreteState. For instance, the bipartition {{1,2},{3}} partitions the QuantumDiscreteState into subsystems {1,2} and {3}.
In ResourceFunction["QuantumEntanglementMonotone"][QuantumDiscreteState[…],bipart,mono], the following entanglement monotones mono are supported:
| "Concurrence" | generalized concurrence monotone for pure states and two-subsystem mixed states |
| "Negativity" | negativity monotone for pure and mixed states (i.e. the Peres–Horodecki separability criterion) |
| "LogNegativity" | logarithmic negativity monotone for pure and mixed states (i.e. the Peres–Horodecki separability criterion) |
| "EntanglementEntropy" | entanglement entropy monotone for pure states (i.e. the von Neumann entropy of the reduced density matrices) |
| "RenyiEntanglementEntropy" | Rényi entanglement entropy monotone with Rényi index α=1/2 for pure states (i.e. the Rényi entropy of the reduced density matrices) |
| {"RenyiEntanglementEntropy",α} | Rényi entanglement entropy monotone with specified Rényi index α for pure states (i.e. the Rényi entropy of the reduced density matrices) |
Whenever the entanglement monotone
mono is not defined for the specified
QuantumDiscreteState,
ResourceFunction["QuantumEntanglementMonotone"] will return
Indeterminate.
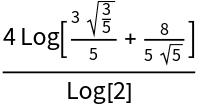
![state = ResourceFunction["QuantumDiscreteState"][{1/Sqrt[3], 0, 0, 0, 1/Sqrt[3], 0, 0, 0, 1/Sqrt[3]}, 3];
ResourceFunction["QuantumEntanglementMonotone"][state, {{1}, {2}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f5d/f5defb75-2038-4518-882f-d83ae7abd92a/0fdff68f3fca2fa8.png)