Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
This resource function is obsolete. Use the paclet Wolfram/QuantumFramework instead.

Function Repository Resource:

 QuantumBasis

Source Notebook

Represent a quantum basis

Contributed by: Jonathan Gorard and Ruhi Shah

ResourceFunction["QuantumBasis"][<|name1→b1,name2→b2,…|>,pic]

represents a discrete quantum basis with basis elements bi, having names namei, with respect to the quantum mechanical picture pic.

ResourceFunction["QuantumBasis"]["name",pic]

represents a named quantum basis "name", with respect to the quantum mechanical picture pic.

ResourceFunction["QuantumBasis"][{"name",d},pic]

represents a d-dimensional version of a named quantum basis "name", with respect to the quantum mechanical picture pic.

ResourceFunction["QuantumBasis"][…,s]

represents a specified quantum basis for a collection of s qudits (subsystems).

ResourceFunction["QuantumBasis"][ResourceFunction["QuantumBasis"][…],pic]

transforms a specified quantum basis into the new quantum mechanical picture pic.

Details

The permitted values of pic in ResourceFunction["QuantumBasis"][assoc,pic], ResourceFunction["QuantumBasis"]["name",pic] and ResourceFunction["QuantumBasis"][{"name",d},pic] are "Schrodinger" (default - may also be written "Schroedinger" or "Schrödinger"), "Heisenberg", "Interaction" and "PhaseSpace".
The keys name$i can be any expression. Typical choices are strings or Ket expressions.
ResourceFunction["QuantumBasis"][…]["prop"] gives the property "prop" of the specified quantum basis. Possible properties include:
"BasisElementNames"list of basis element names namei
"BasisElements"list of basis elements bi
"NormalizedBasisElements"list of normalized basis elements bi
"BasisElementAssociation"the association <| name1→b1,name2→b2,…|>
"MatrixRepresentation"change of basis matrix (from the computational basis)
"Rank"tensor rank of the basis elements bi
"Type"whether the basis elements bi are vectors, matrices or higher-rank tensors
"Dimensions"dimensionality of the basis elements bi
"Qudits"number of qudits (subsystems) in the basis
"Picture"which quantum mechanical picture the basis is defined with respect to
"Properties"list of all property names
ResourceFunction["QuantumBasis"][ResourceFunction["QuantumBasis"][…],s] represents a tensor product of the specified basis with itself s times.
ResourceFunction["QuantumBasis"]["name"] or ResourceFunction["QuantumBasis"][{"name",d}] represents a (d-dimensional) named quantum basis. Possible named bases include:
"Computational"2-dimensional computational basis
{"Computational",d}d-dimensional computational basis
"Bell"Bell basis
"PauliZ"Pauli-Z (computational) basis
"PauliX"Pauli-X (Hadamard) basis
"PauliY"Pauli-Y basis
"Fourier"2-dimensional basis of the quantum Fourier transform
{"Fourier",d}d-dimensional basis of the quantum Fourier transform
"Schwinger"2-dimensional Schwinger basis
{"Schwinger",d}d-dimensional Schwinger basis
"Pauli"basis of the Pauli matrices
"Dirac"basis of the Dirac (gamma) matrices
"Wigner"2-dimensional basis of the Wigner phase space operators with respect to the computational basis
{"Wigner",d}d-dimensional basis of the Wigner phase space operators with respect to the computational basis
{"Wigner",ResourceFunction["QuantumBasis"][…]}basis of the Wigner phase space operators with respect to the specified ResourceFunction["QuantumBasis"]

Examples

Basic Examples (5) 

Create a 2-dimensional basis in the Schrodinger picture (default), using Ket notation for the basis element names:

In[1]:=
basis = ResourceFunction[ "QuantumBasis"][<|Ket[0] -> {1, 0}, Ket[1] -> {0, 1}|>]
Out[1]=

Return its basis element association:

In[2]:=
basis["BasisElementAssociation"]
Out[2]=

Create a 2-dimensional basis in the Heisenberg picture, using strings for the basis element names:

In[3]:=
basis = ResourceFunction[ "QuantumBasis"][<|"a" -> {1, -1}, "b" -> {1, 1}|>, "Heisenberg"]
Out[3]=

Return its matrix representation (change of basis matrix):

In[4]:=
basis["MatrixRepresentation"]
Out[4]=

Basis elements can be tensors of arbitrary rank:

In[5]:=
basis = ResourceFunction[ "QuantumBasis"][<|Ket[0] -> {{1, 0}, {0, 1}}, Ket[1] -> {{0, 1}, {1, 0}}, Ket[2] -> {{0, I}, {-I, 0}}, Ket[3] -> {{1, 0}, {0, -1}}|>]
Out[5]=

Return a matrix representation:

In[6]:=
basis["MatrixRepresentation"]
Out[6]=

Return the rank and type:

In[7]:=
basis["Rank"]
Out[7]=
In[8]:=
basis["Type"]
Out[8]=

Represent the Bell basis for a single qubit (default):

In[9]:=
basis1 = ResourceFunction["QuantumBasis"]["Bell"]
Out[9]=
In[10]:=
basis1["BasisElementAssociation"]
Out[10]=

Represent the Bell basis for a pair of qubits (defined via a tensor product) instead:

In[11]:=
basis2 = ResourceFunction["QuantumBasis"]["Bell", 2]
Out[11]=
In[12]:=
basis2["BasisElementAssociation"]
Out[12]=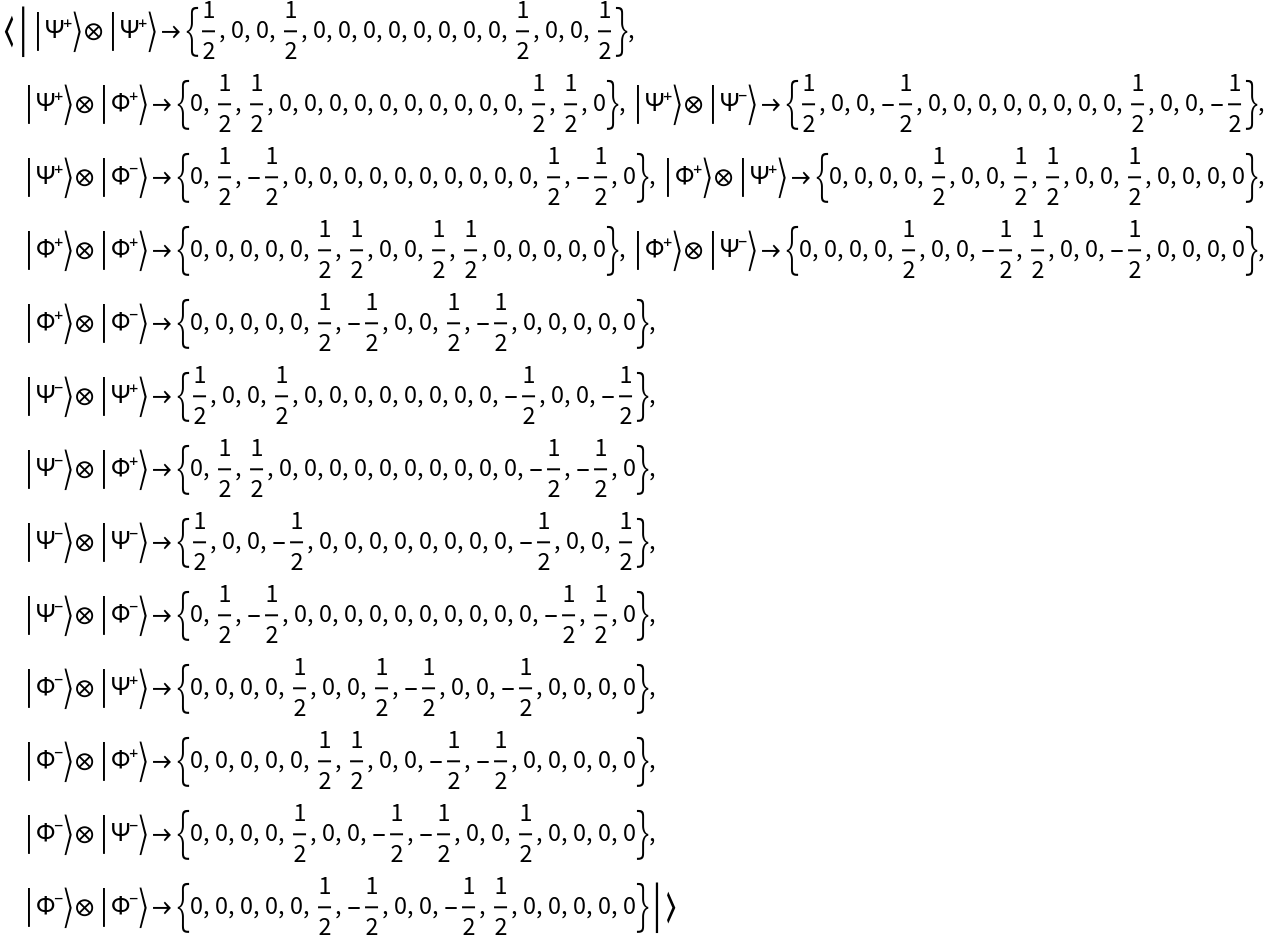

Represent the 2-dimensional (default) basis of the quantum Fourier transform:

In[13]:=
basis1 = ResourceFunction["QuantumBasis"]["Fourier"]
Out[13]=

Get its matrix representation:

In[14]:=
basis1["MatrixRepresentation"]
Out[14]=

Represent the 3-dimensional basis of the quantum Fourier transform instead:

In[15]:=
basis2 = ResourceFunction["QuantumBasis"][{"Fourier", 3}]
Out[15]=

Get its matrix representation:

In[16]:=
basis2["MatrixRepresentation"]
Out[16]=

Scope (9) 

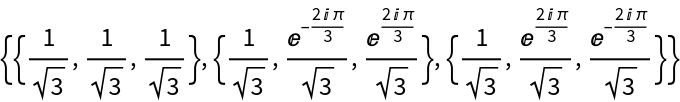The elements of a 2-dimensional QuantumBasis can be arbitrary (potentially non-orthonormal) vectors:

In[17]:=
basis = ResourceFunction[ "QuantumBasis"][<|"a" -> {1, -3}, "b" -> {3, 1}|>]
Out[17]=

Return the list of basis elements:

In[18]:=
basis["BasisElements"]
Out[18]=

Return the list of normalized basis elements:

In[19]:=
basis["NormalizedBasisElements"]
Out[19]=

Represent the Pauli-X (Hadamard) basis in the Heisenberg picture:

In[20]:=
basis = ResourceFunction["QuantumBasis"]["PauliX", "Heisenberg"]
Out[20]=

Transform the basis to the interaction picture:

In[21]:=
ResourceFunction["QuantumBasis"][basis, "Interaction"]
Out[21]=

Create a 2-dimensional basis for a single qubit:

In[22]:=
basis1 = ResourceFunction["QuantumBasis"][<|"a" -> {1, -1}, "b" -> {1, 1}|>]
Out[22]=

Create a 3-qubit version of the same basis by taking a tensor product of the basis with itself 3 times:

In[23]:=
basis2 = ResourceFunction["QuantumBasis"][basis1, 3]
Out[23]=

View the basis elements of the 3-qubit system:

In[24]:=
basis2["BasisElementAssociation"]
Out[24]=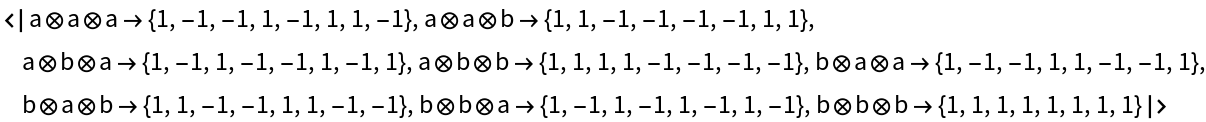

Represent the 2-dimensional Schwinger basis of rank-2 (matrix) elements:

In[25]:=
basis = ResourceFunction["QuantumBasis"]["Schwinger"]
Out[25]=

View the basis elements:

In[26]:=
basis["BasisElementAssociation"]
Out[26]=

Represent the 3-dimensional Schwinger basis:

In[27]:=
basis = ResourceFunction["QuantumBasis"][{"Schwinger", 3}]
Out[27]=

View its basis elements:

In[28]:=
basis["BasisElementAssociation"]
Out[28]=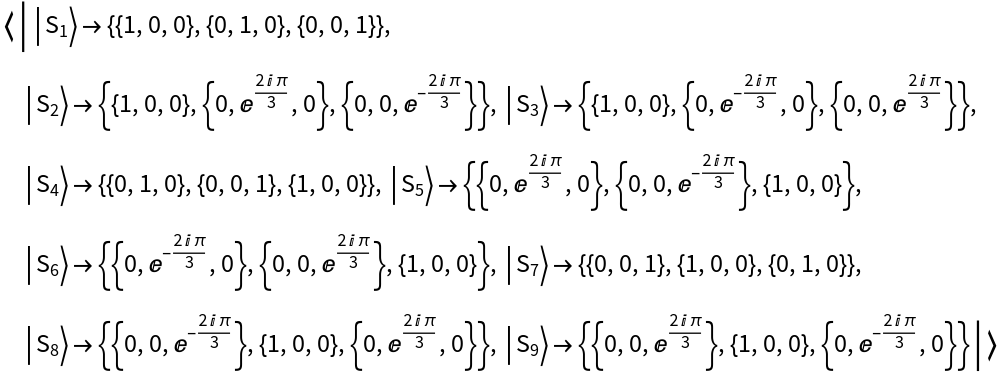

Represent the basis of rank-2 Pauli matrices:

In[29]:=
basis = ResourceFunction["QuantumBasis"]["Pauli"]
Out[29]=

View the basis elements:

In[30]:=
basis["BasisElementAssociation"]
Out[30]=

Represent the basis of rank-2 Dirac (gamma) matrices:

In[31]:=
basis = ResourceFunction["QuantumBasis"]["Dirac"]
Out[31]=

View the basis elements:

In[32]:=
basis["BasisElementAssociation"]
Out[32]=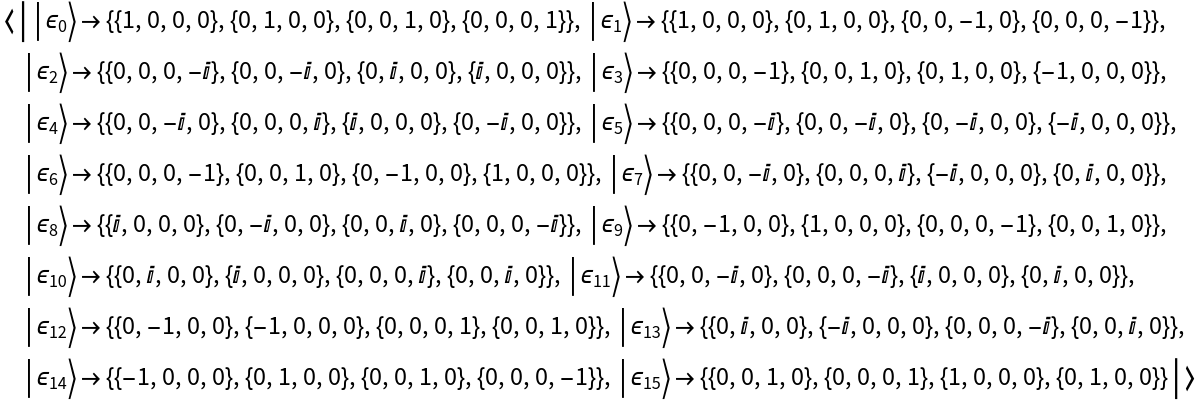

Represent the 2-dimensional basis of Wigner phase space operators with respect to the computational basis:

In[33]:=
basis = ResourceFunction["QuantumBasis"]["Wigner"]
Out[33]=

View the basis elements:

In[34]:=
basis["BasisElementAssociation"]
Out[34]=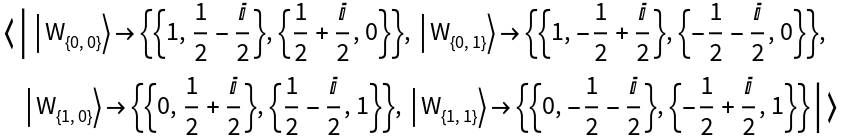

Represent the 3-dimensional basis of Wigner phase space operators with respect to the computational basis:

In[35]:=
basis = ResourceFunction["QuantumBasis"][{"Wigner", 3}]
Out[35]=

View the basis elements:

In[36]:=
basis["BasisElementAssociation"]
Out[36]=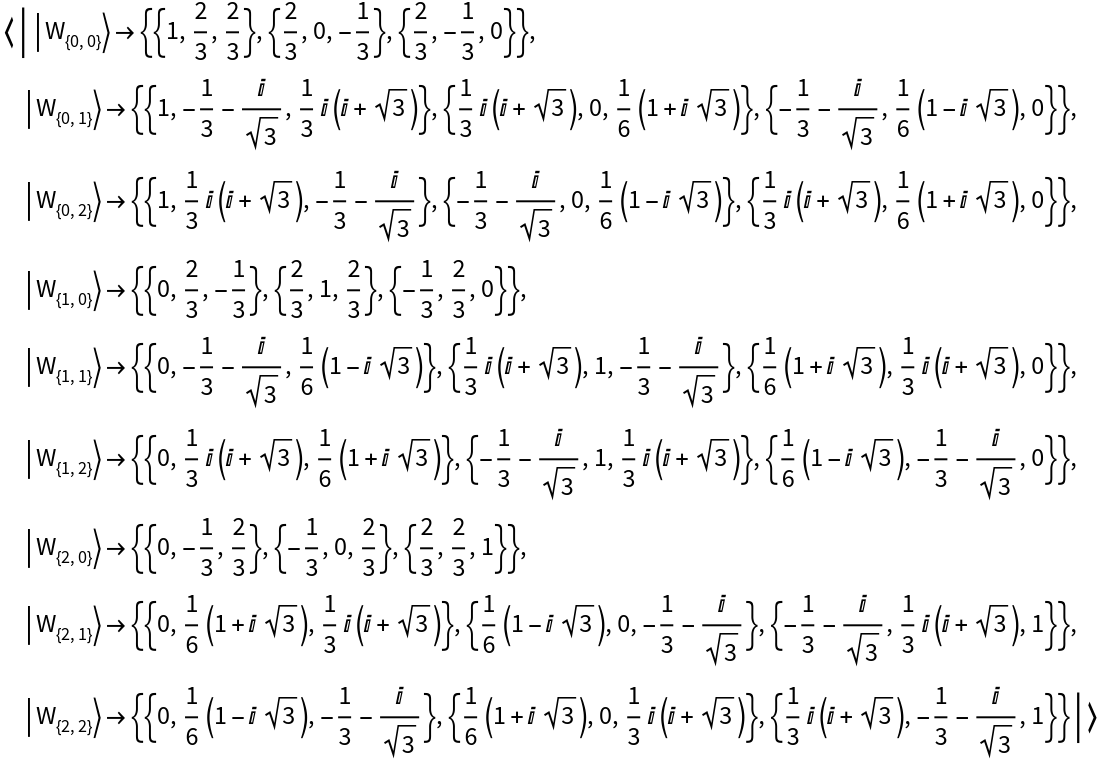

Represent the 2-dimensional basis of Wigner phase space operators with respect to the Pauli-X (Hadamard) basis:

In[37]:=
basis = ResourceFunction[ "QuantumBasis"][{"Wigner", ResourceFunction["QuantumBasis"]["PauliX"]}]
Out[37]=

View the basis elements:

In[38]:=
basis["BasisElementAssociation"]
Out[38]=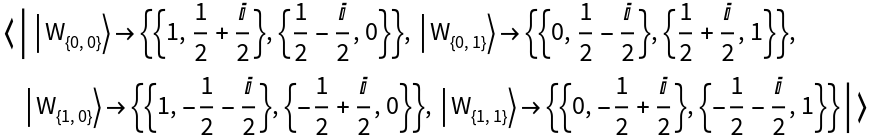

QuantumBasis objects can be constructed purely symbolically (without explicit vector or matrix elements):

In[39]:=
basis1 = ResourceFunction["QuantumBasis"][<|"up" -> {x, y}, "down" -> {z, w}|>, "Heisenberg"]
Out[39]=

View the basis elements:

In[40]:=
basis1["BasisElementAssociation"]
Out[40]=

Standard operations can still be performed on purely symbolic bases:

In[41]:=
basis1["MatrixRepresentation"]
Out[41]=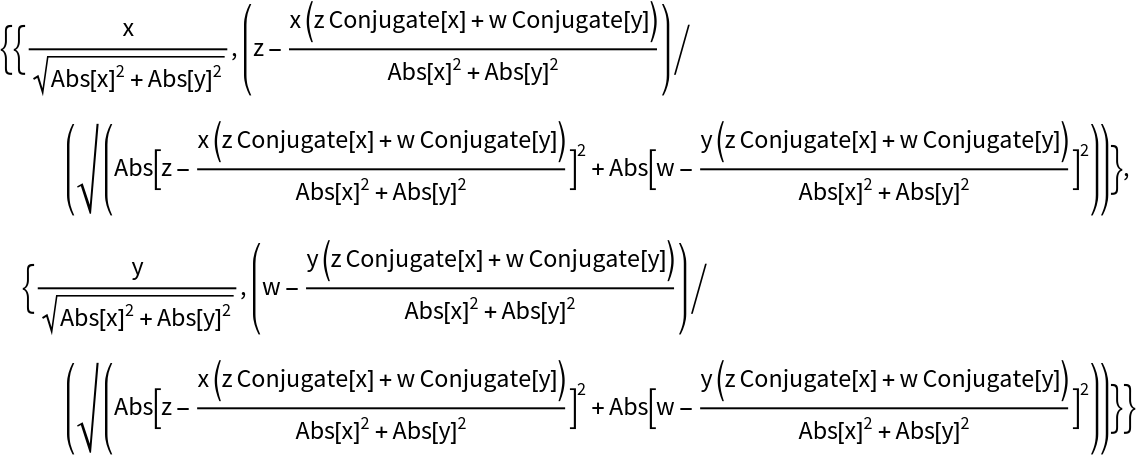

Represent a collection of 2 qudits:

In[42]:=
basis2 = ResourceFunction["QuantumBasis"][basis1, 2]
Out[42]=

View the basis elements:

In[43]:=
basis2["BasisElementAssociation"]
Out[43]=

View a list of properties that can be extracted from a QuantumBasis object:

In[44]:=
basis = ResourceFunction["QuantumBasis"]["Computational", 2]
Out[44]=
In[45]:=
basis["Properties"]
Out[45]=

Return the list of basis element names:

In[46]:=
basis["BasisElementNames"]
Out[46]=

Return the list of basis elements:

In[47]:=
basis["BasisElements"]
Out[47]=

Return the list of normalized basis elements:

In[48]:=
basis["NormalizedBasisElements"]
Out[48]=

Return the association of names and basis elements:

In[49]:=
basis["BasisElementAssociation"]
Out[49]=

Return the matrix representation (change of basis matrix):

In[50]:=
basis["MatrixRepresentation"]
Out[50]=

Return the rank and type of basis:

In[51]:=
basis["Rank"]
Out[51]=
In[52]:=
basis["Type"]
Out[52]=

Return the number of dimensions:

In[53]:=
basis["Dimensions"]
Out[53]=

Return the number of qudits (subsystems):

In[54]:=
basis["Qudits"]
Out[54]=

Return which quantum mechanical picture the basis is defined with respect to:

In[55]:=
basis["Picture"]
Out[55]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 17 March 2021

Related Resources

License Information